
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели механических свойств грунтов
Под механическими свойствами грунтов понимают их способность сопротивляться изменению объема и формы под действием внешних силовых и физических (изменение влажности, температуры и др.) воздействий. Характеристики этих свойств различаются для разных видов и состояний грунтов и зависят от величины действующих напряжений. В допредельном напряженном состоянии характеристики механических свойств называются деформационными. Они определяют способность грунтов сопротивляться развитию деформаций (осадок, горизонтальных смещений и др.). В предельном состоянии характеристики механических свойств называются прочностными и определяют способность грунтов сопротивляться разрушению. Механические свойства грунтов зависят от их состава (гранулометрического, минерального), физического состояния (плотности, влажности) и структурных особенностей, обусловленных условиями образования и последующего изменения под действием природных явлений или техногенной деятельности. Обычно механические свойства грунтов определяются экспериментально: лабораторными или полевыми исследованиями. Иногда показатели механических свойств грунтов могут быть определены косвенным путем по их физическим характеристикам. Так, СНиП 2.02.01-83* "Основания зданий и сооружений" допускает для предварительных расчетов оснований, а также для окончательного расчета оснований зданий и сооружений II и III классов и опор линий электропередач и связи независимо от их класса определять значения прочностных и деформационных характеристик грунтов по показателям их физического состояния. С этой целью в СниП 2.02.01-83* приводятся таблицы нормативных значений прочностных и деформационных характеристик песков и глинистых грунтов. Сжимаемость грунтов
Сжимаемостью грунтов называется их способность уменьшаться в объеме, давая осадку, под действием внешней нагрузки. Сжимаемость происходит в основном за счет уменьшения объема пор, так как твердые минеральные частицы и вода считаются практически несжимаемыми в диапазоне распространенных в строительной практике давлений (0,1-0,5 МПа). Рассмотрим деформации сжатия выделенного в грунте объема, размеры которого таковы, что в его пределах напряжения от действующих на грунт внешних нагрузок постоянны.
Выделенный объем грунта сжимается в направлении большего из действующих напряжений и расширяется в перпендикулярных ему направлениях.Но поскольку расширению грунта препятствует реакция окружающего грунта, то деформация его происходит при ограниченной возможности бокового расширения. В связи с неопределенностью деформации такого вида рассмотрим деформацию грунта при граничных условиях: 1) при свободном боковом расширении и 2) при полной невозможности бокового расширения. В первом случае (рис. 4) относительные деформации грунта будут:
εx = εy = νεz (16) или ν = где εx, εy, εz — относительные деформации грунта по осям X, Y и Z соответственно; ν - коэффициент бокового расширения (коэффициент Пуассона).
Рис. 4. Схема деформации грунта при свободном боковом расширении
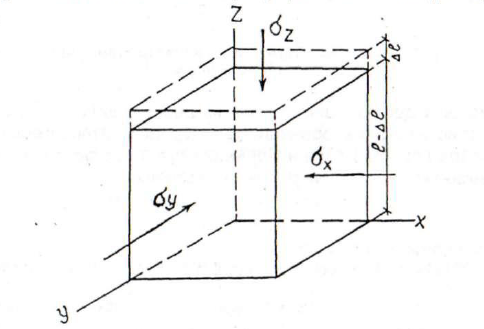
Значения v принимаются равными для грунтов: крупнообломочных - 0,27; песков и супесей - 0,30; суглинков - 0,35; глин - 0,42. При сжатии в условиях полной невозможности бокового расширения (рис. 5) грунты испытывают одноосное сжатие в направлении приложения вертикальной нагрузки Nz и расширение в горизонтальном. Однако этому расширению препятствует реакция окружающего грунта, вызывая горизонтальные сжимающие напряжения σх и σу. Величина бокового давления грунта при невозможности бокового расширения характеризуется коэффициентом бокового давления ζ:
отсюда следует, что Значения коэффициента бокового давления ζ, полученные экспериментально, следующие: для песков - 0,25+0,37; для глинистых грунтов (в зависимости от консистенции) - 0,11+0,82. Для глинистых грунтов текучепластичной консистенции ζ приближается к единице.
Рис. 5. Схема деформации грунта при полной невозможности бокового расширения
Для установления связи между коэффициентом бокового расширения ν и бокового давления ζ к мысленно выделенному в массиве грунта элементарному кубу, находящемуся в равновесии в условиях свободного бокового расширения, приложим вертикальную нагрузку Nz, под действием которой грань куба будет испытывать напряжение σZ, вызывающее деформацию боковых граней куба. Не снимая напряжения σZ, к боковым граням куба приложим нагрузки Nx и Ny, вызывающие напряжения по граням σX и σY. При этом σX = σY=ζ∙σZ. Напряжения σX и σY создадут дополнительное обжатие грунта, возвращая боковые грани куба в первоначальное состояние. Так как объем куба под действием этих напряжений остается постоянным, то сумма деформаций будет равна нулю.
Рассмотрим деформацию одного из ребер I куба (например, по оси X) от действующих напряжений (рис. 6). Если относительное удлинение ребра I при действии напряжения составит ε, то напряжение σZ вызывает удлинение ребра на величину
где
Рис. 6. Деформация грунта от действия напряжений по трем направлениям
Действие напряжения
Так как сумма деформаций равна нулю, то
отсюда,
Решая равенство, получим
откуда
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 728; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.144.32 (0.01 с.) |
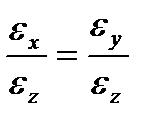 (16')
(16')
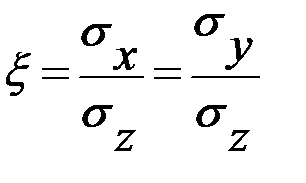 ,
,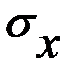


 ,
, - коэффициент Пуассона.
- коэффициент Пуассона. Под действием напряжения
Под действием напряжения  ребро I удлинится на величину
ребро I удлинится на величину
 вызывает сжатие ребра I на величину
вызывает сжатие ребра I на величину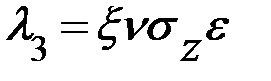
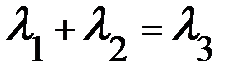
 +
+ 
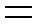
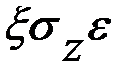
 +
+ 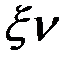 =
=  ;
;  ,
,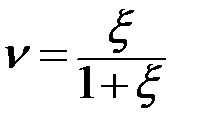 ;
; 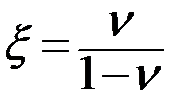 , (17)
, (17)


