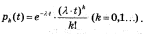Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деякі наслідки теореми Чебишева. ⇐ ПредыдущаяСтр 3 из 3
Теорема Пуасона: нехай задано послідовність незалежних спроб. В i-ій ймовірність появи події А = pi; m – число появ події A в n спробах. Тоді для довільного e>0:
Доведення: зведемо до теореми Чебишева. Для цього розглянемо послідовність випадкових змінних ti=1, якщо подія A відбулась в спробі i, 0 – якщо не відбулась. Тоді D(t) <= ¼. Всі умови теореми Чебишева виконуються.
Якщо в теоремі Пуасона покласти pi = P, то вийде теорема Бернуллі.
Теорема Маркова: як і т. Чебишева, але змінні як завгодно залежні і Доведення: на основі т. Чебишева. Характеристична функція випадкової змінної Характеристичну фукцію випадкової змінної можна отримати, застосувавши до неї перетворення Фур’є. Таким чином характеристична функція це є мат. сподівання e^(ist), i=sqrt(-1), s – параметр. В випадку неперервної випадкої змінної характеристична функція має вигляд int(x=-INF..INF) {e^(isx)f(x)dx}, в випадку дискретної SUM(k){e^(isXk)*Pk}. Властивості: · |phi(s)| <= 1 · phi(0)=1 · лінійно перетворена випадкова змінна y=a*x+b має характер e^(i*b*s)*phi(a*s) · характер суми випадкових змінних = добутку їх характерів · якщо випадкова змінна має мат. сподівання і характер, то вони визначаються формулами: E(t) = ln(phi(0))́́ /i; D(t) = -ln(phi(0))́́˝ Властивості характеристичних функцій. (Див. 31) Взаємно однозначна відповідність між функцією розподілу і характеристичною функцією Доводиться, що
Тоді покажемо, що Доведення:
Обмежник – функція, яка на інтервалі рівна 1, а ззовні інтервалу = 0. Точковий обмежник – всюди, крім деякої точки рівний 0, а в цій точці = 1.
Т. Нехай випадкова змінна має функцію приросту F, хар. ф-ю f. Тоді
Т. Нехай випадкова змінна має характеристичну функцію f. Тоді функція розподілу буде визначатись так:
Доведення: так, як і в попередній теоремі, але b=x, a -> -INF. Теореми про суми характеристичних функцій Т. Сума біномно розподілених незалежних випадкових змінних – біномно розподілена. Доведення: справді, хар. функція має вигляд (p*e^(is)+q)^n. Тоді phi(x+y) = phi(x)*phi(y) = (p*e^(is)+q)^n1 * (p*e^(is)+q)^n2 = (p*e^(is)+q)^(n1+n2)
Т. Сума пуасонівсько розподілених незалежних випадкових змінних буде пуасонівсько розподіленою. Доведення: справді, хар. функція має вигляд e^(L1*(e^(is)-1)).
Тоді phi(x+y) = phi(x)*phi(y) = e^(L1*(e^(is)-1)) * e^(L2*(e^(is)-1)) = e^((L1+L2)*(e^(is)-1))
аналогічно, для нормально розподілених, гама-розподілених. Стохастичні процеси, ланцюг Маркова. Стохастичний процес – це процес, реалізація якого залежить від випадку, і для якого визначена ймовірність того, чи іншого, перебігу.
Нехай в послідовності незалежних спроб в кожній спробі може виникнути одна з деяких подій E1,…,Ek. Нехай після n проків стались події Ei1, Ei2,…, Ein. Цю складну подію будем називати конфігурація. Послідовність спроб утворює ланцюг Маркова, якщо для довільної конфігурації
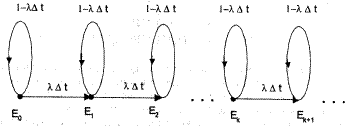
Вектор з невід’ємними компонентами, сума яких = 1 називається стохастичним. Квадратна матриця з невід’ємними компонентами, сума по кожному рядку в якій = 1 наз. стохастичною. Отже ланцюг Маркова – коли задано стохастичний вектор і стохастичну матрицю. Вектор – ймовірності в початковий момент часу. Матриця – ймовірності переходу в наступні моменти часу. Ймовірність переходу зі стану в стан за n кроків. Нехай ймовірність переходу зі стану Ei в стан Ej є P(n) ij. Знайдемо цю ймовірність методом мат. індукції. При n=1 P(n) ij = P. При n=2 маємо наступне: ми перейшли з стану i в деякий стан k і з нього в стан j. Тому P(n) ij = SUM(k) Pik * Pkj. Ця матриця стохастична. Для кроку індукції аналогічно: P(n) ij = SUM(k) P(n-1) ik * P(n-1) kj. Стаціонарний розподіл ланцюга Маркова. Нехай існують граничні ймовірності перебування системи в стані k: lim (n->INF) p(n) k = pk. Потрібно знайти pk. Перейдемо в рівняння p(n)*P = p(n+1) до границі при n->INF, тоді: p*(P-I) = 0. Розв’язавши цю систему рівнянь, і врахувавши, що p – стохастичний вектор, отримаємо стаціонарний розподіл ланцюга Маркова. Пуасонівський процес. Нехай деяка система може перебувати в деяких станах Е1,Е2, …, Ek, причому, якщо в деякий момент часу t вона перебуває в стані Ek, то за час ∆t вона буде перебувати в стані E(k+1) з ймовірністю L*∆t + o(∆t), L>0 (L=const). З імовірністю 1- L*∆t + o(∆t) вона залишиться в стані Ek, і з ймовірностями o(∆t) вона перейде в інші стани. В початковий момент часу вона знаходиться в стані 0. Цей процес можна зобразити наступним графом:
Щоб побудувати модель процесу перейдемо до границі при ∆t -> 0, отримаємо:
Розв’язавши цю задачу Коші, отримаємо Таким чином ми знайшли розподіл ймовірностей перебування системи в стані k в час t.
|
||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.190.144 (0.008 с.) |

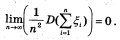 , то має місце висновок з теореми Чебишева.
, то має місце висновок з теореми Чебишева. .
.