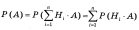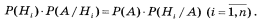Теореми про ймовірність суми подій.

Т. Ймовірність появи несумісних подій дорівнює сумі ймовірностей цих подій:

P(A+B) = P(A) + P(B), якщо A*B=V

Доведення:

Нехай повна сукупність рівно можливих несумісних подій складається з n елементарних подій. Нехай A розпадається на k сприятливих подій, B – на m сприятливих подій. Оскільки А і В несумісні, то немає подій, які сприятливі для A i B одночасно. Тому

P(A+B) = (k + m)/n = k/n + m/n = P(A) + P(B).

 

Т. Ймовірність суми двох подій рівна сумі їх ймовірностей мінус ймовірність їх суміщення.

P(A+B) = P(A) + P(B) – P(A*B)

Доведення: з діаграм Вена. (або алгебраїчно через суму несумісних)

Умовні ймовірності (ймовірності добутку подій)

Якщо ймовірність виконання події А залежить від виконання іншої події В, то ймовірність появи події А в цьому випадку називається умовною ймовірністю. P(A/B) – ймовірність події А, за умови, що відбулась подія В.

 

Т. Ймовірність добутку двох подій рівна добутку ймовірності однієї на умовну ймовірність другої, за умови, що відбулась перша:

P(A*B) = P(A)* P(A/B) = P(B)* P(B/A)

Доведення: Нехай події E₁,E₂,…,E_n утворюють повну сукупність рівноможливих подій, з яких r сприятливі для A, s – для B, m – для А і В одночасно. Тоді

P(A*B) = m/n = (m/s) * (s/n) = P(B)*P(B/A)

P(A*B) = m/n = (m/r) * (r/n) = P(A)*P(A/B).

Незалежні події

Якщо подія А не змінює ні сукупності умов S, ні сприятливих подій для події B, то подія B називається незалежною від події А.

Формальніше можна сказати так:

Подія А незалежна від події В, якщо P(A/B) = P(A). Аналогічно: подія В незалежна від події А, якщо P(В/А) = P(В).

 

Отже, з теореми про добуток подій отримуємо, що для незалежних подій

P(A*B) = P(A)*P(B).

Т. Якщо подія А не залежить від події В, то і подія В не залежить від події А.

Доведення: Якщо P(A/B) = P(A), то P(A*B) = P(B) * P(A/B) = P(A)*P(B) = P(A)*P(B/A) => P(B) = P(B/A) => B не залежить від А.

Незалежні в сукупності події

Якщо подій більше двох, то вони можуть бути попарно залежні, незалежні, можуть зустрічатись ті чи інші види залежності в підмножинах подій.

 

Події А1,А2,…,An називаються незалежні в сукупності, якщо для будь-якої підмножини їх A_i1­­­­­, A_i2, …, A_ik виконується P(A_i1* A_i2*…* A_ik) = P(A_i1) * P(A_i2) * … * P(A_ik).

 

Це означає, що події можуть бути попарно незалежні, а в сукупності – ні.

Формула повної ймовірності

Повна сукупність несумісних подій – якщо вони попарно несумісні і хоча б одна з них точно відбувається.

 

Т. Нехай задана повна сукупність несумісних подій H1,H2,…,Hn, і подія А може відбутись лише в парі з однією з цих подій. Тобто: А = H1*A + H2*A + … + Hn*A. Тоді H1,H2,…,Hn називаються гіпотезами, а ймовірність події А обчислюється так:

Доведення: Якщо події H1,H2,…,Hn попарно несумісні, то попарно несумісні будуть і події Hi*A (i=1..n). Тому з теореми про добуток несумісних подій маємо:

а з теореми про ймовірність залежних подій:

Це і є формула повної ймовірності.

7. Формула гіпотез (формула Байєса)

Нехай задана повна сукупність несумісних подій H1,H2,…,Hn, і подія А може відбутись лише в парі з однією з цих подій. Тобто: А = H1*A + H2*A + … + Hn*A. Тоді H1,H2,…,Hn називаються гіпотезами. Нехай тепер відомо, що подія А відбулась, обчислимо P(Hi/A), тобто уточнити ймовірності гіпотез, виходячи з того факту, що подія А відбулась.

 

З теореми про ймовірність залежних подій маємо:

Звідси, і з формули повної ймовірності отримуємо:

Остання формула і називається формулою Байєса. Ймовірності P(Hi) називаються апріорні, а P(Hi/A) – апостеріорні.

Залежні події. Регресія. Кореляція.

Кажуть, що подія А залежить від події В, якщо P(A)!= P(A/B). Це означає, що подія А змінює або комплекс умов S, або набір сприятливих подій для події B.

 

Коефіцієнт регресії події А відносно події В є мірою залежності подій, і обчислюється так:

p(A,B) = P(A/B) – P(A/!B)

Аналогічно і події В відносно події А:

 

Т. Якщо коефіцієнт регресії = 0, то події незалежні, і навпаки, якщо події незалежні, то = 0.

Доведення: Якщо події незалежні, то P(A/B) = P(A/!B) = P(A) => коеф. регресії = 0.

Якщо коефіцієнт регресії = 0, то P(A/B) = P(A/!B) тоді з означення умовної ймовірності: P(A*B)/P(B) = P(A*!B) / P(!B), тоді P(A*B)*(1-P(B)) = (P(A)-P(A*B))*P(B) => P(A)*P(B)=P(A*B) => A і B незалежні.

 

Коефіцієнт кореляції подій А і В називається величина:

Властивості коефіцієнту кореляції:

· між еквівалентними подіями = 1

· між протилежними подіями = -1

· між незалежними подіями = 0, і навпаки, якщо = 0, то незалежні.

· R(A,B) = R(B,A)

· -1 <= R(A,B) <= 1

· R(A,B) = R(!A,!B)

· R(A,B) = -R(!A,B) = -R(A,!B)