
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание дсв и нсв и его свойства. Формулы их расчета. ⇐ ПредыдущаяСтр 2 из 2
Математическое ожидание (МОж) – характеристика положения ожидаемой величины; мера среднего значения СВ. Мож ДСВ = сумме произведений возможных значений постоянных величин на вероятность ее появления. Для СВ с конечным числом значений Мож существует, а при бесчисленном, но счетном множестве значений Мож может не существовать. Св-ва: 1) x min<M(X)<x max 2) Y= KX K=const M(Y)=KM(X) Если СВ умножить на постоянный коэффициент К, то ее МОж увеличится в К раз. 3) M(C)=C C=const 4) 5) M(Y+/- X)=M(X) +/- M(Y) (для независимых СВ) 6)
Для НСВ: М(х) = Понятие и определение моды, медианы, дисперсии и среднеквадратического отклонения СВ. Формулы расчета. Что они характеризуют? Модой Мо(Х) НСВ X называют то значение х, при котором плотность вероятности наибольшая. Модой Мо(Х) ДСВ X называют такое значение СВ, при котором вероятность его наступления наибольшая.
Для НСВ Р (Х> Me) = Р (Х< Me)= 0,5
Дисперсия – степень разброса СВ относительно ее Мож.
D(X)= M(X - M(X)) = M(X) - (M(X))
Cреднеквадратическое (стандартное) отклонение СВ
Определение вероятности попадания нормально распределенной СВ на произвольный интервал. Выведете формулу для этого случая CВ Х распределена по нормальному закону, если ее f(x) описывается функцией Гаусса или имеет вид: f(x)=(1/ где m=M(X) Предположим, что мы хотим определить вероятность того, что СВ Х, распределенная по нормальному закону, попадет на интервал (
Как определить вероятность попадания нормально распределенной СВ на интервал, симметричный относительно Мож? Выведете эту формулу Очень часто приходится вычислять вероятность отклонения СВ от М(Х) по модулю, т.е. чтобы отклонение СВ от М(Х) по модулю не превышало |x-m|< P(|x-m|<
x-m /
 / / 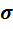
P(|x-m|< 29. Основные задачи и определения математической статистики. Мат.статистика - мат.дисциплина для анализа данных. В современных условиях мат.ст. определяют как теорию принятия решений в условиях вероятностной (стохастической) неопределенности. Цель: по результатам выборочных данных вынести суждение о св-вах генеральной совокупности. Ген.совокупность- все мыслимые значения (элементы) СВ при заданных условиях. Множество значений или элементов ген.сов-ти может быть конечным или бесконечным (счетным или несчетным). Выборка объема n- определенная совокупность значений независимых СВ, извлеченных из генеральной совокупности в количестве n. Задачи: 1) Разработка методов сбора и группировки выборочных данных; 2) Разработка методов анализа выборочных данных: § Оценка неизвестной вероятности появления события; § Оценка неизвестных параметров распределения, вид которого неизвестен; § Оценка зависимости СВ от одной или нескольких СВ. 3) Проверка статистических гипотез; 4) Разработка методов планирования экспериментов до начала исследования или в ходе его проведения. Способы обеспечения результативности выборки: · Простой отбор – последовательно случайно отбирают первый, а затем последующие элементы выборки; · Типический отбор – отбор пропорционально численности отдельных видов элементов, содержащихся в ген.сов-ти; · Случайный отбор – с помощью таблиц случайных чисел или датчика случайных чисел отбирают элементы в выборку.
Понятие точечной оценки параметров закона распределения вероятностей СВ. Требования, предъявляемые к точечным оценкам. Почему от точечных оценок параметров закона распределения переходят к интервальным? Точечная оценка – оценка, имеющая конкретное числовое значение. Требования: 1) Несмещенность 2) Состоятельность 3) Эффективность Несмещенной называют точечную оценку, Мож которой = оцениваемому параметру при любом объеме выборки. Оценка называется эффективной, если она обладает минимальной D(X) среди всех возможных несмещенных точечных оценок.
Оценка называется состоятельной, если она по вероятности с увеличением объема n стремится к параметру генеральной совокупности.
Все точечные оценки параметров распределения СВ являются сами СВ. Знание закона распределения СВ(оценки) позволяет нам ответить на вопрос о том, с какой точностью мы оценили неизвестный параметр закона распределения СВ. Но эти законы распределения (оценок) в свою очередь зависят от неизвестных параметров закона распределения, поэтому очень часто от законов распределения оценок переходят к законам распределения некоторых других СВ, которые связаны с оценками параметров, но законы распределения которых не зависят от оцениваемых параметров. Эти СВ называются статистиками. При выборке малого объема точечная оценка может знач.отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1859; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.130 (0.009 с.) |
 X+C M(X+C)=M(X)+C C=const
X+C M(X+C)=M(X)+C C=const
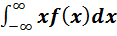
 Пример: 1,2,4,2,5,7,2 Мо=2 (т.к. Р=3/7)
Пример: 1,2,4,2,5,7,2 Мо=2 (т.к. Р=3/7) =
=  =0,5
=0,5

 Геометрически медиану можно истолковать как точку, в которой ордината f(х) делит пополам площадь, ограниченную кривой распределения.
Геометрически медиану можно истолковать как точку, в которой ордината f(х) делит пополам площадь, ограниченную кривой распределения.
 a=M(X)=
a=M(X)= 
 =
=  a=M(X)
a=M(X)

 )*
)*  для НСВ
для НСВ =D(X)
=D(X) ).
).
 .
.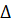 )
) -
-  = Z
= Z -
-  /
/  /
/ 


