Как вычислить вероятность попадания СВ в заданный интервал Для дсв и нсв.

Приведите определение и классификацию СВ. Пример СВ в экономике.

СВ- величина, которая в результате опыта в зависимости от случая принимает одно из возможного множества своих значений, которое заранее не известно.

СВ делятся на 2 класса:

1) Дискретные СВ

2) Непрерывные СВ

Дискретная СВ - величина, когда множество ее значений конечное или бесконечное, но счетное.

Непрерывная СВ – величина, когда множество ее значений бесконечное и несчетное.

 

Примеры случайных величин.

1. Совокупный доход страны складывается из доходов отдельных граждан, которые склонны утаивать размер дохода. Поэтому совокупный доход – величина случайная.

2. Вкладывая деньги в покупку акций на финансовом рынке, мы точно не знаем, повысится ли их стоимость в будущем или нет. Поэтому стоимость акций – величина случайная.

3. Страховая компания, продавая вам страховой полис, не знает наверняка, случится ли что-либо с вашим здоровьем или имуществом.

4. Точно также в повседневной жизни: спрос индивидуума на какой-либо товар может быть совершенно случайным, но совокупный спрос на товар может быть спрогнозирован.

 

21. Приведите определение дискретной и непрерывной СВ. Закон распределения ДСВ и формы их задания

Дискретная СВ - величина, когда множество ее значений конечное или бесконечное, но счетное.

Непрерывная СВ – величина, когда множество ее значений бесконечное и несчетное.

Закон распределения - всякое соотношение устанавливающее взаимосвязь между множествами значений СВ и соответствующими вероятностями.

Заданное соответствие между возможными значениями ДСВХ и их вероятностями называется законом распределения дискретной случайной величины.

Для ДСВ закон распределения может быть задан в табличной форме, в аналитической форме(формула) и в графической форме. Графическую форму чаще всего называют полигоном распределения или многоугольником распределения.

1) При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности:

 

Хi	x1	x2	…	хi	xn
р i	p1	p2	…	pi	pn

Эта таблица называется рядом распределения.

2) Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события Х=х1, Х=х2, …, Х=хn - образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:

Если множество возможных значений Х бесконечно (счетно), то ряд сходится и его сумма равна единице.

P(X=xi)=Pi i=1,n

 

3) Ряд распределения можно представить графически, если по оси абсцисс отложить возможные значения ДСВХ, а по оси ординат - соответствующие вероятности. Соединив полученные точки отрезками, получим ломаную, называемую многоугольником распределения вероятностей.

 

 

х1х2 хn

22. Функция распределения вероятности для НСВ, ее формула, определения и св-ва. Какие задачи она позволяет решать?

Функцией распределения F(x) CB(X) является функция F(x), определяющяя для каждого значения х вероятность того, что СВ(Х) примет значение < х.

F(x) = P (X <x)

Для НСВ ф-ция распределения F(X) является непрерывной и дифференцированной всюду, за исключением быть может отдельных точек.

Вероятность того, что непрерывная случайная величина X примет одно определенное значение равна нулю:

F(X =хi)= 0.

Св-ва:

1) 0 ≤ F(x) ≤ 1

2)

F(x2)

F(x) неубывающая функция своего аргумента.

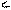
X2

X1

F(x1)

F(x2)-F(x1) ≥0

x2>x1 x

P(x1 ≤ x < x2)

 

F(x2)= F(x1)+P(x1 ≤ x < x2)

F(x2)-F(x1)=P(x1 ≤ x < x2) ≥0

3) Вероятность попадания СВ на интервал [х1;х2) равна приращению функции распределения на этом интервале.

P(x1 ≤ x < x2) = F(x2)-F(x1)

 

4)

 

Задачи:

позволяют по заданной вероятности вычислить такое значение х, при котором вероятность равна или меньше заданного значения.

 

23. Понятие плотности распределения вероятности. Формула для ее определения через функцию распределения вероятности. Свойства плотности вероятности. Какие задачи она позволяет решать?

Плотностью распределения вероятности f(x) HCB называют производную ее функции распределения.

F ' (x) = f(x) =

F(x) =

Св-ва:

1) f(x)≥ 0

2) в-ть попадания НСВ в интервал [(а;b)] = определенному интегралу от ее плотности вероятности в пределах от a до b.

3) Функция распределения НСВ определяется как плотность вероятности по формуле

F ' (x) = f(x) =

4) = 1

Задачи:

Зная плотность распределения, можно найти функцию распределения

F (х) =

Для НСВ

Р (Х> Me) = Р (Х< Me)= 0,5

Геометрически медиану можно истолковать как точку, в которой ордината f(х) делит пополам площадь, ограниченную кривой распределения.

 

Ме

 

Дисперсия – степень разброса СВ относительно ее Мож.

a=M(X)=

Для НСВ если нам известна f(x), то

D(X)= M(X - M(X)) = M(X) - (M(X))

Для ДСВ D(X)= = a=M(X)

Cреднеквадратическое (стандартное) отклонение СВ

Понятие точечной оценки параметров закона распределения вероятностей СВ. Требования, предъявляемые к точечным оценкам. Почему от точечных оценок параметров закона распределения переходят к интервальным?

Точечная оценка – оценка, имеющая конкретное числовое значение.

Требования:

1) Несмещенность

2) Состоятельность

3) Эффективность

Несмещенной называют точечную оценку, Мож которой = оцениваемому параметру при любом объеме выборки.

Оценка называется эффективной, если она обладает минимальной D(X) среди всех возможных несмещенных точечных оценок.

Оценка называется состоятельной, если она по вероятности с увеличением объема n стремится к параметру генеральной совокупности.

 

Все точечные оценки параметров распределения СВ являются сами СВ. Знание закона распределения СВ(оценки) позволяет нам ответить на вопрос о том, с какой точностью мы оценили неизвестный параметр закона распределения СВ. Но эти законы распределения (оценок) в свою очередь зависят от неизвестных параметров закона распределения, поэтому очень часто от законов распределения оценок переходят к законам распределения некоторых других СВ, которые связаны с оценками параметров, но законы распределения которых не зависят от оцениваемых параметров. Эти СВ называются статистиками.

При выборке малого объема точечная оценка может знач.отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Метод мах правдоподобия

Заключается в отыскании мах функций одного или нескольких параметров.

Если имеется объем выборки, то по теореме умножения вероятностей для независимых СВ, мы можем записать ф-цию правдоподобия.

L(x; )= f(x1; ) * f(x2; ) *… *f(xn; )= П f(xi; )

Оценки параметров законов распределения полученные по методу мах правдоподобия являются состоятельными и ассимптотически эффективными. Кроме того эти оценки асимптотически распределены по нормальному закону. При n >30, распределение оценок близко к нормальному.

33. Выведете формулы для точечных оценок параметров нормально распределенной СВ, используя метод моментов. Каким требованиям удовлетворяют эти оценки?

Метод моментов

Заключается в приравнивании теоретических моментов к соответствующим эмперическим моментам того же порядка.

2 типа моментов: начальные и цетральные

Оценки, получаемые по методу моментов, являются состоятельными, но не всегда эффективными.

Приведите определение и классификацию СВ. Пример СВ в экономике.

СВ- величина, которая в результате опыта в зависимости от случая принимает одно из возможного множества своих значений, которое заранее не известно.

СВ делятся на 2 класса:

1) Дискретные СВ

2) Непрерывные СВ

Дискретная СВ - величина, когда множество ее значений конечное или бесконечное, но счетное.

Непрерывная СВ – величина, когда множество ее значений бесконечное и несчетное.

 

Примеры случайных величин.

1. Совокупный доход страны складывается из доходов отдельных граждан, которые склонны утаивать размер дохода. Поэтому совокупный доход – величина случайная.

2. Вкладывая деньги в покупку акций на финансовом рынке, мы точно не знаем, повысится ли их стоимость в будущем или нет. Поэтому стоимость акций – величина случайная.

3. Страховая компания, продавая вам страховой полис, не знает наверняка, случится ли что-либо с вашим здоровьем или имуществом.

4. Точно также в повседневной жизни: спрос индивидуума на какой-либо товар может быть совершенно случайным, но совокупный спрос на товар может быть спрогнозирован.

 

21. Приведите определение дискретной и непрерывной СВ. Закон распределения ДСВ и формы их задания

Дискретная СВ - величина, когда множество ее значений конечное или бесконечное, но счетное.

Непрерывная СВ – величина, когда множество ее значений бесконечное и несчетное.

Закон распределения - всякое соотношение устанавливающее взаимосвязь между множествами значений СВ и соответствующими вероятностями.

Заданное соответствие между возможными значениями ДСВХ и их вероятностями называется законом распределения дискретной случайной величины.

Для ДСВ закон распределения может быть задан в табличной форме, в аналитической форме(формула) и в графической форме. Графическую форму чаще всего называют полигоном распределения или многоугольником распределения.

1) При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности:

 

Хi	x1	x2	…	хi	xn
р i	p1	p2	…	pi	pn

Эта таблица называется рядом распределения.

2) Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события Х=х1, Х=х2, …, Х=хn - образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:

Если множество возможных значений Х бесконечно (счетно), то ряд сходится и его сумма равна единице.

P(X=xi)=Pi i=1,n

 

3) Ряд распределения можно представить графически, если по оси абсцисс отложить возможные значения ДСВХ, а по оси ординат - соответствующие вероятности. Соединив полученные точки отрезками, получим ломаную, называемую многоугольником распределения вероятностей.

 

 

х1х2 хn

22. Функция распределения вероятности для НСВ, ее формула, определения и св-ва. Какие задачи она позволяет решать?

Функцией распределения F(x) CB(X) является функция F(x), определяющяя для каждого значения х вероятность того, что СВ(Х) примет значение < х.

F(x) = P (X <x)

Для НСВ ф-ция распределения F(X) является непрерывной и дифференцированной всюду, за исключением быть может отдельных точек.

Вероятность того, что непрерывная случайная величина X примет одно определенное значение равна нулю:

F(X =хi)= 0.

Св-ва:

1) 0 ≤ F(x) ≤ 1

2)

F(x2)

F(x) неубывающая функция своего аргумента.

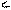
X2

X1

F(x1)

F(x2)-F(x1) ≥0

x2>x1 x

P(x1 ≤ x < x2)

 

F(x2)= F(x1)+P(x1 ≤ x < x2)

F(x2)-F(x1)=P(x1 ≤ x < x2) ≥0

3) Вероятность попадания СВ на интервал [х1;х2) равна приращению функции распределения на этом интервале.

P(x1 ≤ x < x2) = F(x2)-F(x1)

 

4)

 

Задачи:

позволяют по заданной вероятности вычислить такое значение х, при котором вероятность равна или меньше заданного значения.

 

23. Понятие плотности распределения вероятности. Формула для ее определения через функцию распределения вероятности. Свойства плотности вероятности. Какие задачи она позволяет решать?

Плотностью распределения вероятности f(x) HCB называют производную ее функции распределения.

F ' (x) = f(x) =

F(x) =

Св-ва:

1) f(x)≥ 0

2) в-ть попадания НСВ в интервал [(а;b)] = определенному интегралу от ее плотности вероятности в пределах от a до b.

3) Функция распределения НСВ определяется как плотность вероятности по формуле

F ' (x) = f(x) =

4) = 1

Задачи:

Зная плотность распределения, можно найти функцию распределения

F (х) =

Как вычислить вероятность попадания СВ в заданный интервал для ДСВ и НСВ?

Вероятность попадания НСВ в интервал [(а;b)] = определенному интегралу от ее плотности вероятности в пределах от a до b.

P(a<X<b) =

Вероятность попадания ДСВ на интервал [х1;х2) равна приращению функции распределения на этом интервале.

P(x1 ≤ x < x2) = F(x2)-F(x1)