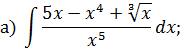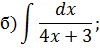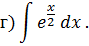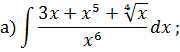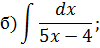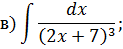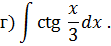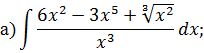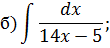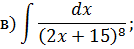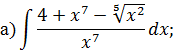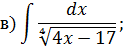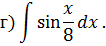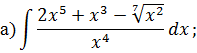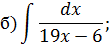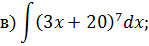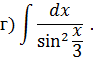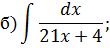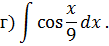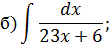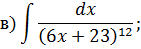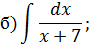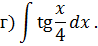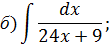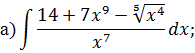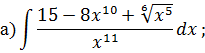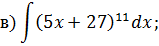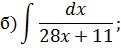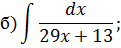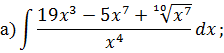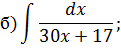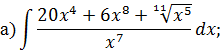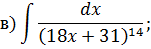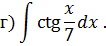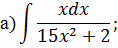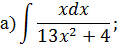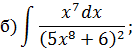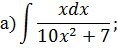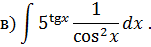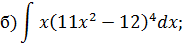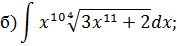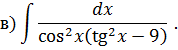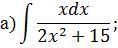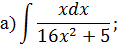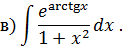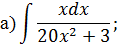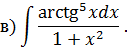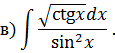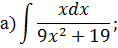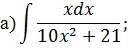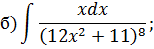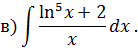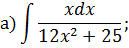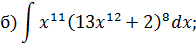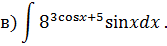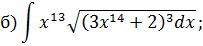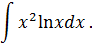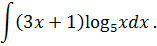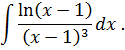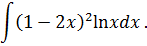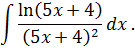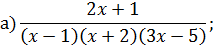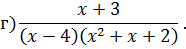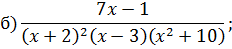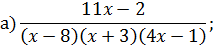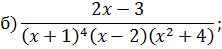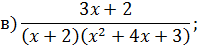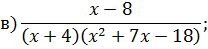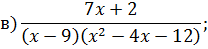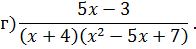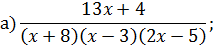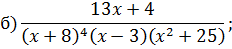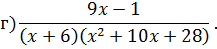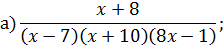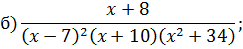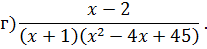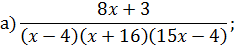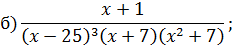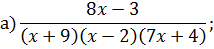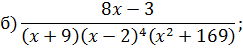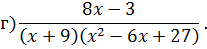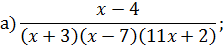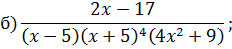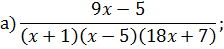Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод замены переменной в неопределенном интегралеСтр 1 из 3Следующая ⇒
ВВЕДЕНИЕ Цель преподавания математики – ознакомить курсанта (студента) с основами математического аппарата, необходимого для решения теоретических и практических задач, привить курсантам (студентам) умение самостоятельно изучать учебную литературу по математике и её приложениям, развить логическое мышление и повысить общий уровень математической культуры. В достижении этой цели помогают типовые расчеты (ТР). Данное пособие содержит типовой расчет по интегральному исчислению функции одной и нескольких переменных и предназначен для курсантов первого курса. Типовой расчет содержит теоретические вопросы, которые являются общими для всех курсантов, и расчетные задачи – индивидуальные для каждого курсанта. Всего предлагается 30 различных вариантов задач. Помимо перечисленных пунктов пособие содержит решение типового варианта. Выполнение курсантами (студентами) ТР контролируется преподавателем. Задачи сдаются курсантами на проверку в письменном виде. Завершающим этапом является защита ТР. Во время защиты курсант должен уметь правильно отвечать на теоретические вопросы, пояснять решения задачи, решать задачи аналогичного типа.
КОНТРОЛНЫЕ ВОПРОСЫ 1. Первообразная функции 2. Неопределенный интеграл. 3. Геометрический смысл неопределенного интеграла. 4. Свойства неопределенного интеграла. 5. Закончить формулы:
6. Укажите одну из первообразных функции 7. Формула интегрирования по частям в неопределенном интеграле. 8. Геометрический и физический смысл определенного интеграла. 9. Формула Ньютона-Лейбница. 10. Отличие метода замены переменной в неопределенном и определенном интеграле. 11. Формула интегрирования по частям в определенном интеграле. 12. Несобственные интегралы первого и второго рода. 13. Двойной интеграл. 14. Геометрический и физический смысл двойного интеграла. 15. Криволинейный интеграл 1 и 2 рода.
Решение типового варианта Табличное интегрирование Задача 1. Найти интегралы: Решение. 1) Для нахождения данного интеграла сначала осуществить почленное деление числителя на знаменатель в подынтегральной функции, выполнить действия со степенями, применяя формулы
и далее использовать формулу интеграла от степенной функции
2), 3), 4) Для нахождения данных интегралов используется формула
Метод замены переменной в неопределенном интеграле Задача 2. Найти неопределенные интегралы:
или воспользоваться формулой
Интегрирование по частям в неопределенном интеграле Задача 3. Найти неопределенный интеграл Решение. Для нахождения данного интеграла используется метод интегрирования по частям, основанный на формуле
Интегрирование тригонометрических функций Задача 6. Найти интегралы:
Решение. 1) Интегралы вида
2) Интегралы вида
3) Интегралы вида
Методы замены переменной и интегрирования по частям В определенном интеграле Задача 7. Вычислить интегралы:
Решение. 1) Использовать метод замены переменной:
2) Использовать метод интегрирования по частям:
Задача 8. Исследовать несобственные интегралы на сходимость. В случае их сходимости вычислить: следовательно, интеграл расходится. 2) При
)
Тогда
следовательно, интеграл расходится. Кратные интегралы Повторный интеграл Задача 11. Вычислить повторный интеграл:
Решение. Сначала вычисляется внутренний интеграл, где у является переменной, а х постоянной:
Полученный результат подставить под знак внешнего интеграла и проинтегрировать его по переменной х.
Таким образом,
Двойной интеграл Задача 12. Привести двойной интеграл
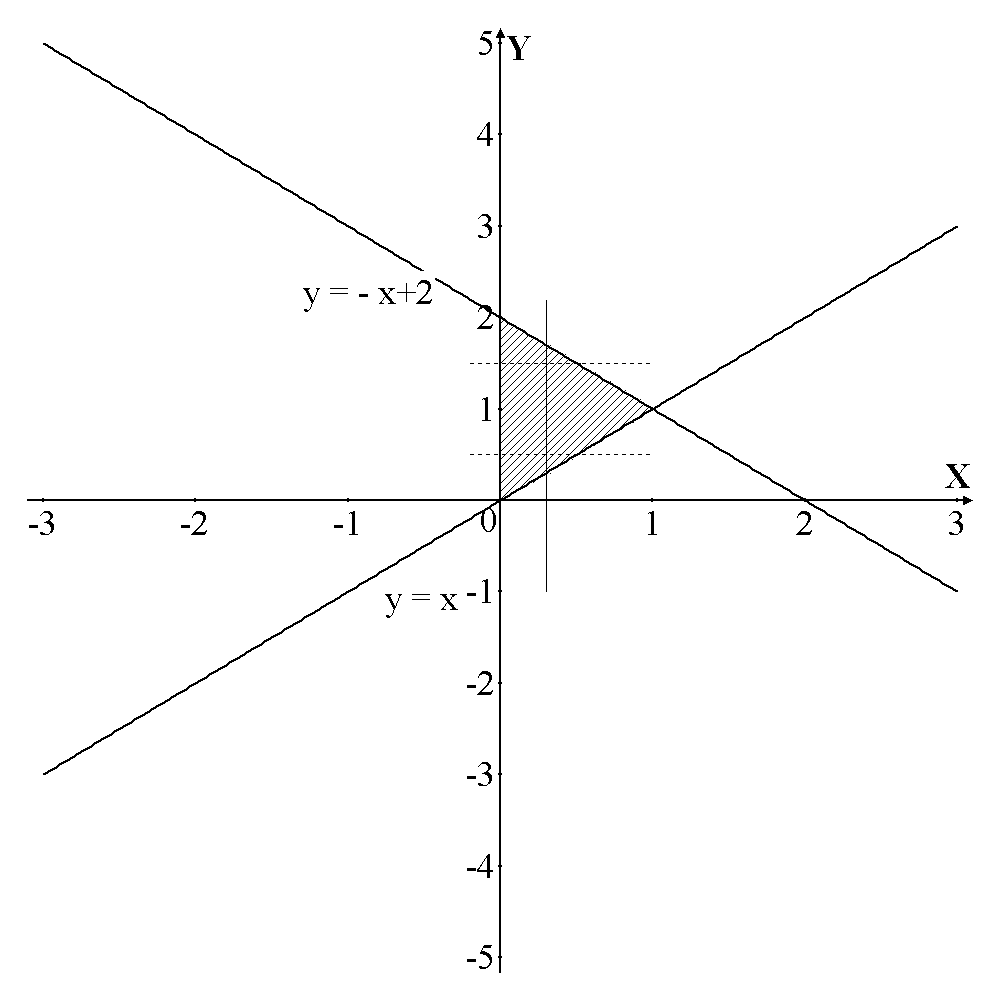
по области D к повторному двумя способами и вычислить его. Решение. Вычисление двойного интеграла начинается с изображения области интегрирования. Все линии, ограничивающие область, необходимо построить и подписать (рис.3).
Рис. 3 Следующий шаг – переход от двойного интеграла к повторному. Для этого необходимо выбрать порядок интегрирования в повторном интеграле, т.е. Чтобы выбрать наиболее удобный для вычисления порядок интегрирования, надо посмотреть, относительно какой оси нет «узлов» (то есть точек стыка различных линий). В нашем случае относительно оси О х нет «узлов», поэтому в таком порядке как Для того чтобы найти внешние пределы интегрирования, нужно спроецировать крайние точки области на ось, дифференциал которой стоит под знаком внешнего интеграла. В нашем случае ─ на ось О х, т.к. имеет место
1) Сначала вычисляется внутренний интеграл, где y является переменной, а х постоянной:
2) Затем вычисляется внешний интеграл, подставив в него результат вычисления внутреннего интеграла.
При расстановке пределов вторым способом получается следующий результат
Криволинейный интеграл НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Задача 1. Табличное интегрирование.
Задача 2. Используя метод замены переменной, найдите интегралы:
Задача 3. Используя метод интегрирования по частям, найдите интегралы:
Задача 4. Разложить дробь на простейшие, используя метод неопределенных коэффициентов.
Задача 5. Найдите интегралы от рациональных функций:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.156.140 (0.052 с.) |
 на множестве
на множестве  .
. …
… …
… …
…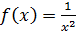 .
.





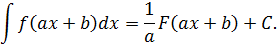


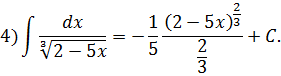


 , тогда
, тогда



 .
. . За «и» принимается тот множитель, от которого нет табличного интеграла, или тот, который после дифференцирования станет проще, все остальное принимается за «dv».
. За «и» принимается тот множитель, от которого нет табличного интеграла, или тот, который после дифференцирования станет проще, все остальное принимается за «dv».


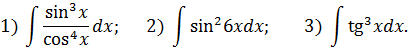

 берутся с помощью подстановки. Для этого от функции, стоящей в нечетной положительной степени отделить множитель и кофункцию для него обозначить новой переменной.
берутся с помощью подстановки. Для этого от функции, стоящей в нечетной положительной степени отделить множитель и кофункцию для него обозначить новой переменной.






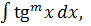
 берутся с помощью подстановки соответственно
берутся с помощью подстановки соответственно 







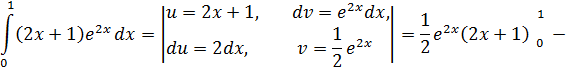
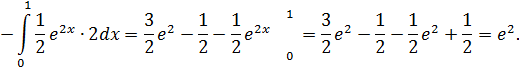


 , то есть при приближении x к нижнему пределу интегрирования, подынтегральная функция
, то есть при приближении x к нижнему пределу интегрирования, подынтегральная функция  неограниченно возрастает, а в самой точке
неограниченно возрастает, а в самой точке  терпит разрыв. Промежуток непрерывности для данной функции будет иметь вид:
терпит разрыв. Промежуток непрерывности для данной функции будет иметь вид: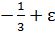 1
1






 или
или  .
.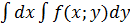 будет один повторный интеграл.
будет один повторный интеграл.
 , выход на линии
, выход на линии  ). Таким образом,
). Таким образом,