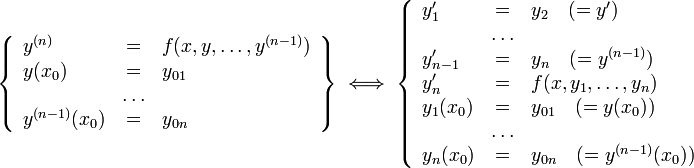Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о дифференциальном уравнении. Задача Коши
Определение 1. Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением. Определение 2. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения. Дифференциальное уравнение n -го порядка имеет вид F(x,y,y ', y '', …, y (n))=0. Определение 3. Дифференциальное уравнение n -го порядка называется линейным, если неизвестная функция и все ее производные входят в него в первой степени. Общий вид линейного дифференциального уравнения n -го порядка: a 0 (x)y (n) + a 1 (x)y (n-1) +... + a n-1 (x)y (1) + a n (x)y = f(x). (1) Определение 4. Линейное дифференциальное уравнение (1) называется однородным, если f(x) º 0, и неоднородным - в противном случае. Примеры дифференциальных уравнений: y'' - sin x y' + ( cos x) y = tg x - линейное, sin y' - cos y = ctg x - нелинейное, y''' - y' = 0- линейное, (y IV ) 2 - 3 y''' + y = 1 - нелинейное. Определение 5. Решением дифференциального уравнения называется любая функция y = j(x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.
y' = f(x), y' = C, y = ò f(x)dx + C. y = C 1 x + C 2. Определение 6. Решение дифференциального уравнения n -го порядка, содержащее n произвольных постоянных, называется общим решением дифференциального уравнения. Определение 7. Если в результате интегрирования дифференциального уравнения получена зависимость между y и x, из которой не удается явно выразить y через x (т.е. неизвестная функция задана неявно), то данную зависимость называют общим интегралом дифференциального уравнения. Определение 8. Решение, полученное из общего при конкретных значениях произвольных постоянных, называется частным решением. Пример. y'' + y = 0. y = C 1cos x + C 2sin x - общее решение. у 1 = 3cos x -2sin x - частное решение. Задача Коши [править] Материал из Википедии — свободной энциклопедии Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач. Основные вопросы, которые связаны с задачей Коши, таковы: 1. Существует ли (хотя бы локально) решение задачи Коши? 2. Если решение существует, то какова область его существования? 3. Является ли решение единственным? 4. Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных? Говорят, что задача Коши имеет единственное решение, если она имеет решение
[править]Различные постановки задачи Коши § ОДУ первого порядка, разрешённое относительно производной
§ Система
§ ОДУ
Дифференциальные уравнения с разделяющимися переменными
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.110.169 (0.005 с.) |
 Пример 1. y' - f(x) = 0, Пример 2. y'' = 0,
Пример 1. y' - f(x) = 0, Пример 2. y'' = 0,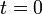 , а решение отыскивается при
, а решение отыскивается при 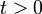 .
.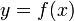 и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки
и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки 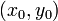 имеет поле направлений, совпадающее с полем направлений
имеет поле направлений, совпадающее с полем направлений 
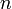 ОДУ первого порядка, разрешённая относительно производных (нормальная система
ОДУ первого порядка, разрешённая относительно производных (нормальная система