
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная формула комбинаторикиСтр 1 из 4Следующая ⇒
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*...*nk. Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6). Итак, N=n1*n2*n3=6*7*4=168.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8? Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625.
Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений обозначается Anm и вычисляется по формуле:
Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1. Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные? Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
2. горох Классическое и геометрическое определение вероятностей. Условная вероятность Пример Игральная кость подбрасывается один раз. Известно, что выпало более трёх очков. Какова вероятность того, что выпало чётное число очков? Зная, что выпало более трёх очков, мы можем сузить множество всех возможных элементарных исходов до трёх одинаково вероятных исходов: Посмотрим на вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Мы хотим найти, какую часть составляют исходы, благоприятствующие
Мы пришли к выражению, которое можно считать определением условной вероятности. Решение. Пусть А – попадание первого стрелка, В – попадание второго стрелка, Тогда
Найдем нужные вероятности. а) АВ – двойное попадание, б) в) А + В – хотя бы одно попадание,
г)
7. Формула полной вероятности. Пусть событие А может произойти только совместно с одним из событий Н 1, Н 2,…, Нп, образующих полную группу несовместных событий. Тогда события Н 1, Н 2,…, Нп называются гипотезами . Теорема. Вероятность события А, наступающего совместно с гипотезами Н 1, Н 2,…, Нп, равна: где P (Hi) – вероятность i той гипотезы, а P (A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула носит название формулы полной вероятности.
Доказательство. Можно считать событие А суммой попарно несовместных событий АН 1, АН 2,…, АНп. Тогда из теорем сложения и умножения следует, что что и требовалось доказать. 8. Формула Байеса. Пусть
Доказательство. По определению условной вероятности,
9. Сводка основных правил теории вероятности.
10. Схема с повторением независимых испытаний (схема Бернулли). Формула Бернулли. Испытания независимы, если вероятность элементарных исходов не зависят от предыдущих испытаний.
Доказательство:
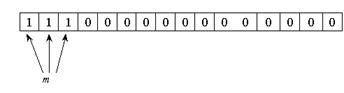
Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность [править]Доказательство Так как в результате Обозначим
При этом вероятность каждой комбинации равна произведению вероятностей:
Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:
11. Теорема Пуассона. Функция Лапласа. Интегральная формула Муавра-Лапласа. Теорема Пуассона.Пусть есть
Тогда
Функция Лапласа
Правило трех сигм В теории вероятностей квадратичное отклонение σx случайной величины x (от ее математического ожидания) определяется как квадратный корень из дисперсии Dx и называют также стандартным отклонением величины x. Для любой случайной величины x с математическим ожиданием mx и квадратичным отклонением σx вероятность отклонения x от mx, больших по абсолютной величине k·σx, k > 0, не превосходит 1/k2 (неравенство Чебышева). В случае нормального распределения указанная вероятность при k = 3 равна 0.0027. В практических задачах, приводящих к нормальному распределению, чаще всего пренебрегают возможностью отклонения от среднего, большего 3·σx.
18. Закон распределения Пуассона. Функция надежности. Интенсивность отказов. Показательный закон. Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)). Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию.
Пусть элемент (то есть некоторое устройство) начинает работать в момент времени t0 = 0 и должен проработать в течение периода времени t. Обозначим за Т непрерывную случайную величину — время безотказной работы элемента, тогда функция F (t) = p (T > t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна R (t) = p (T > t) = 1 — F (t). Эта функция называется функцией надежности. 19. Центральная предельная теорема.
Центральная Предельная Теорема 1 Пусть
где
20. Закон Больших чисел.
Теорема Чебышева Теорема. Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное числоe, вероятность неравенства будет сколь угодно близка к единице, если число случайных величин достаточно велико.
Т.е. можно записать:
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается: Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины. Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий. Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются. Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности. 23. Следствие из теоремы Чебышева. Если дисперсии независимых случайных величин ограничены одной и той же постоянной С, то, как бы мало не было данное положительное число Е, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий а1, а2, …, аn не превзойдет по абсолютной величине Е, как угодно близка к единице, если число случайных величин достаточно велико.
Следствие. Если независимые случайные величины имеют одинаковые, равные a, математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число случайных величин достаточно велико, то, сколько мало ни было данное положительное число Е, как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от а не превзойдет по абсолютной величине Е. При доказательстве теоремы Чебышева и следствия из нее с помощью неравенства Чебышева получаем такие оценки:
24. Закон больших чисел в форме Бернулли. (ЗБЧ Бернулли). Пусть событие
Доказательство. Заметим, что
и Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством 25. Случайные векторы. Совместный закон распределения двух случайных величин. Горох!))) Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*...*nk. Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6). Итак, N=n1*n2*n3=6*7*4=168.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8? Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625.
Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений обозначается Anm и вычисляется по формуле:
Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1. Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов. Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
2. горох
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.123 (0.066 с.) |

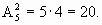
 , из которых событию
, из которых событию  благоприятствуют ровно два:
благоприятствуют ровно два:  . Поэтому
. Поэтому 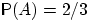 .
. . Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие
. Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие  . Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении
. Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении  происходит и
происходит и  . Вероятность события
. Вероятность события  .
.
 ;
; .
. - промах первого,
- промах первого, 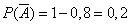 ;
; - промах второго,
- промах второго, 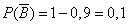 .
.
 .
. .
. – одно попадание,
– одно попадание, 

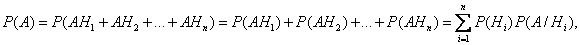
 — полная группа событий, и
— полная группа событий, и  , если в результате эксперимента наблюдалось событие
, если в результате эксперимента наблюдалось событие 

 – число независимых испытаний
– число независимых испытаний  – может произойти с вероятностью
– может произойти с вероятностью  С какой вероятностью событие
С какой вероятностью событие  раз
раз , где
, где  – вероятность неуспеха
– вероятность неуспеха  – число сочетаний способов
– число сочетаний способов

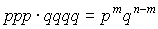
 того, что событие A наступит k раз в n независимых испытаниях, равна:
того, что событие A наступит k раз в n независимых испытаниях, равна:  , где
, где  .
. независимых испытаний, проведенных в одинаковых условиях, событие
независимых испытаний, проведенных в одинаковых условиях, событие  наступает с вероятностью
наступает с вероятностью  , следовательно противоположное ему событие с вероятностью
, следовательно противоположное ему событие с вероятностью 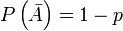 .
. — наступление события
— наступление события 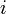 . Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате
. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате  раз, тогда остальные
раз, тогда остальные  раз это событие не наступает. Событие
раз это событие не наступает. Событие  .
. .
.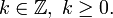 Пусть также дана последовательность
Пусть также дана последовательность  такая, что
такая, что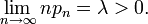



 -- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим
-- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим  и
и 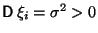 . Тогда
. Тогда 

 -- функция распределения стандартного нормального закона.
-- функция распределения стандартного нормального закона. , (63)
, (63)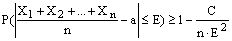
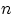 независимых испытаний с одной и той же вероятностью
независимых испытаний с одной и той же вероятностью 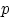 , и пусть
, и пусть  — число осуществлений события
— число осуществлений события  . При этом для любого
. При этом для любого 

 (индикаторовтого, что в соответствующем испытании произошло
(индикаторовтого, что в соответствующем испытании произошло  , где
, где
 ,
, 
 .
.


