
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятности
Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте. Пусть производится опыт с n равнозначными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными исходами (событиями), случаями, шансами. Случай, который приводит к наступлению события А, называется благоприятным (или благоприятствующим) ему. Вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, к общему числу n случаев. p(A)=m/n Такое определение вероятности называется классическим определение вероятности. Из классического определения следуют свойства вероятности: · 0≤p(A)≤1 · p(Ø)=0, · p(Ω)=1, · p(Ā)=1-p(A) · p(A+B)= p(A)+ p(B), если AB=Ø Геометрическое определение вероятности Обобщением понятия "классической вероятности" на случай опытов с бесконечным (вообще говоря, несчетным) числом исходов является понятие "геометрической вероятности". К этому понятию приводят задачи на подсчет вероятности попадания точки в некую область (отрезок, часть плоскости, часть тела и т.д.). Пусть пространство элементарных событий Ω представляет собой некоторую область плоскости. Тогда в качестве событий могут рассматриваться области А, содержащиеся в Ω. Вероятность попадания в область А точки, наудачу выбранной из области Ω, называется геометрической вероятностью события А и находится по формуле: p(A)=S(Ω)/S(Ω), где S(A) и S(Ω) площади областей А и Ω соответственно. Случай, когда Ω представляет собой отрезок или трехмерную область, рассматривается аналогично.
4. Действия над событиями. Алгебра Буля. Действия над случайными событиями и отношения между ними определяются по аналогии с действиями и отношениями в теории множеств. Обозначаем Равенство (эквивалентность) событий: А = В, если А О: Суммой Произведением АВ (А
Примеры: 1. А— выигрыш по займу 1; В — выигрыш по займу 2. Тогда А 2. А — прохождение I тура на конкурсе, В — прохождение II тура. Тогда АВ — успешное прохождение I и II туров. 3. Бросают монету. А — выпадение герба, Множество случайных событий А О: События А и В называются несовместными, если наступление А исключает наступление В, т.е. АВ= Таким образом А, О: Множество (система) событий называется полной группой событий S, если
5. Теорема для сложения вероятностей для совместных событий. Теорема для сложения вероятностей не совместных событий. Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p (A + B)= p (A)+ p (B)− p (AB) Доказательство: A + B = AB + AB + AB (сумма несовместных пар) Тогда p (A + B)= p (AB)+ p (AB)+ p (AB) Событие A = AB + AB, Событие B = AB + AB p (A + B)= p (A)− p (AB)+ p (B)− p (AB)+ p (AB)= p (A)+ p (B)− p (AB)
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В).
Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В. Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1 + m2. Следовательно, Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n.
Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончательно получим Р (А + В) = Р (А) + Р (В).
6. Условная вероятность. Пример. Теорема умножения вероятностей для зависимых событий. Независимые события. Теорема умножения для независимых величин. Условная вероятность
Пример Игральная кость подбрасывается один раз. Известно, что выпало более трёх очков. Какова вероятность того, что выпало чётное число очков? Зная, что выпало более трёх очков, мы можем сузить множество всех возможных элементарных исходов до трёх одинаково вероятных исходов: Посмотрим на вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Мы хотим найти, какую часть составляют исходы, благоприятствующие
Мы пришли к выражению, которое можно считать определением условной вероятности.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.2.15 (0.049 с.) |
 А, если
А, если  — элементарный исход события А; А
— элементарный исход события А; А  В, если событие А влечет за собой В; А, В
В, если событие А влечет за собой В; А, В 
 В и В
В и В 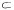 А.
А. событий A и В называется их теоретико-множественное объединение, т.е. событие, состоящее из элементарных событий
событий A и В называется их теоретико-множественное объединение, т.е. событие, состоящее из элементарных событий  или В.
или В. 
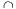 В) событий А и В называется их теоретико-множественное пересечение, т.е. событие, состоящее из элементарных событий:
В) событий А и В называется их теоретико-множественное пересечение, т.е. событие, состоящее из элементарных событий:  А и
А и  В. Разностью
В. Разностью 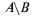 событий Аи В называется их теоретико-множественная разность, т.е. событие, состоящее из элементарных событий
событий Аи В называется их теоретико-множественная разность, т.е. событие, состоящее из элементарных событий  но
но  В. Противоположным событием
В. Противоположным событием 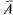 для события A
для события A  называется теоретико-множественное дополнение А до
называется теоретико-множественное дополнение А до  т.е.
т.е.  происходит тогда, когда А не происходит.
происходит тогда, когда А не происходит.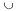 В — выигрыш хотя бы по одному из займов (в частности, сразу по двум).
В — выигрыш хотя бы по одному из займов (в частности, сразу по двум). — выпадение решки.
— выпадение решки. и
и 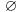 образуют булеву алгебру — алгебру событий, связанных с заданным экспериментом.
образуют булеву алгебру — алгебру событий, связанных с заданным экспериментом. В этом случае используют А
В этом случае используют А  В = А+ В.
В = А+ В.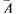 — несовместные события.
— несовместные события.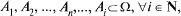


 , из которых событию
, из которых событию  благоприятствуют ровно два:
благоприятствуют ровно два:  . Поэтому
. Поэтому 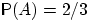 .
. . Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие
. Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие  . Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении
. Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении  происходит и
происходит и  . Вероятность события
. Вероятность события  .
.



