
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение исходного опорного решенияСтр 1 из 2Следующая ⇒
Транспортная задача Транспортная задача — одна из распространенных задач линейного программирования. Ее цель - разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. В общем виде задачу можно представить следующим образом: в т. пунктах производства A 1, A 2,..., Am имеется однородный груз в количестве соответственно a 1, a 2 ,…, am. Этот груз необходимо доставить в п пунктов назначения B 1, В 2, …., Вп в количестве соответственно b 1, b 2 ,..., bп. Стоимость перевозки единицы груза (тариф) из пункта Ai в пункт Bj равна cij. Требуется составить план перевозок, позволяющий вывезти все грузы и имеющий минимальную стоимость. В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
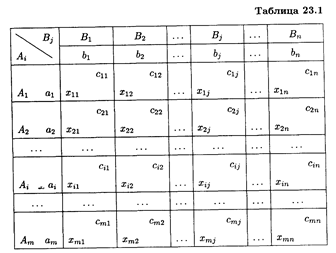
З адача называется закрытой, если: открытой, если: Рассмотрим закрытую транспортную задачу. Обозначим через xij количество груза, перевозимого из пункта Ai в пункт Bj. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения.
при ограничениях:
Оптимальным решением задачи является матрица, удовлетворяющая системе ограничений и доставляющая минимум целевой функции.
Транспортная задача как задача линейного программирования может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими. Поэтому для решения транспортных задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно: 1. Нахождение исходного опорного решения; 2. Проверка этого решения на оптимальность; 3. Переход от одного опорного решения к другому.
Приложение транспортных моделей к решению некоторых экономических задач Алгоритм и методы решения транспортной задачи могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов сij имеют различный смысл в зависимости от конкретной экономической задачи. К таким задачам относятся следующие:
~ оптимальное закрепление за станками операций по обработке деталей. В них cij является таким экономическим показателем, как производительность. Задача позволяет определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей. Так как транспортная задача требует нахождения минимума, то значения cij берутся с отрицательным знаком; ~ оптимальные назначения, или проблема выбора. Имеется т механизмов, которые могут выполнять т различных работ с производительностью cij. Задача позволяет определить, какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности; ~ задача о сокращении производства с учетом суммарных расходов на изготовление и транспортировку продукции; ~ увеличение производительности автомобильного транспорта за счет минимизации порожнего пробега. Уменьшение порожнего пробега сократит количество автомобилей для перевозок, увеличив их производительность; ~ решение задач с помощью метода запрещения перевозок. Используется в том случае, если груз от некоторого поставщика по каким-то причинам не может быть направлен одному из потребителей. Данное ограничение можно учесть, присвоив соответствующей клетке достаточно большое значение стоимости, тем самым в эту клетку не будут производиться перевозки. Выбор оптимального варианта использования производственного оборудования
Производительность каждой группы станков на каждую операцию задана матрицей Решение. Воспользуемся алгоритмом решения закрытой транспортной задачи (табл. 23.13). Так как в задаче требуется найти максимум, а согласно алгоритму транспортной задачи находится минимум, тарифы умножим на (—1).
Клетка (1;2). -8+0-(-5)=-3.
Полученное перераспределение грузов занесем в табл. 23.14. Оценки свободных клеток составляют
Найденное решение является оптимальным, так как все оценки свободных клеток отрицательные. Таким образом, на первой группе станков целесообразно выполнять операции 1 и 4 продолжительностью 40 и 60 ч соответственно, на второй группе — операции 1, 2 и 3 продолжительностью 60, 120 и 70 ч соответственно, на третьей группе — операции 4 и 5 продолжительностью 50 и 130 ч соответственно. При этом максимальное число обработанных деталей составит 5 170 шт. УПРАЖНЕНИЯ
6. Решить транспортную задачу, заданную распределительной табл. 23.16, причем перевозки от 2-го поставщика ко 2-му потребителю и от 3-го поставщика к 1-му потребителю временно закрыты (в таблице эти тарифы обозначены большим числом М > 0).
В связи с неплатежеспособностью перевозки от первого пункта производства до первого пункта потребления и от второго пункта производства до третьего пункта потребления временно закрыты. Составить оптимальный план перевозок, при котором суммарные затраты на них минимальные.
Участок по изготовлению имеет три станка, на каждом из которых можно делать любой из заказанных видов продукции с одинаковой производительностью. Однако единичные затраты по каждому виду продукции различны в зависимости от используемого станка и заданы табл. 23.17. Кроме того, известно, что производственные мощности 2-го и 3-го станков на следующую неделю составят 3000 шт., а 1-го станка — 2000 шт. Используя модель транспортной задачи, найти план производства для заказанных видов продукции, имеющий наименьшую стоимость.
Транспортная задача Транспортная задача — одна из распространенных задач линейного программирования. Ее цель - разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. В общем виде задачу можно представить следующим образом: в т. пунктах производства A 1, A 2,..., Am имеется однородный груз в количестве соответственно a 1, a 2 ,…, am. Этот груз необходимо доставить в п пунктов назначения B 1, В 2, …., Вп в количестве соответственно b 1, b 2 ,..., bп. Стоимость перевозки единицы груза (тариф) из пункта Ai в пункт Bj равна cij.
Требуется составить план перевозок, позволяющий вывезти все грузы и имеющий минимальную стоимость. В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
З адача называется закрытой, если: открытой, если: Рассмотрим закрытую транспортную задачу. Обозначим через xij количество груза, перевозимого из пункта Ai в пункт Bj. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения.
при ограничениях:
Оптимальным решением задачи является матрица, удовлетворяющая системе ограничений и доставляющая минимум целевой функции.
Транспортная задача как задача линейного программирования может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими. Поэтому для решения транспортных задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно: 1. Нахождение исходного опорного решения; 2. Проверка этого решения на оптимальность; 3. Переход от одного опорного решения к другому.
Нахождение исходного опорного решения Условия задачи и ее исходное опорное решение записываются в распределительной таблице. Клетки, в которые поместим грузы, называются занятыми, им соответствуют базисные переменные опорного решения. Остальные клетки незанятые, или пустые, им соответствуют свободные переменные. В верхнем правом углу каждой клетки записываются тарифы. Существует несколько способов нахождения исходного опорного решения. Метод минимального тарифа (элемента). Грузы распределяются в первую очередь в те летки, в которых находится минимальный тариф перевозок cij. Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем т+ п - 1. В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми.
Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждых строке и столбце было не менее чем по одной занятой клетке. Пример 1. Определение эффективного варианта доставки изделий к потребителю
Очевидно, что, данная транспортная задача закрытая. Найдем исходное опорное решение по методу минимального тарифа.
Число занятых клеток в табл. 23.2 равно т + п - 1 = 3 + 3 – 1 = 5.
Стоимость перевозки при исходном опорном решении составляет
|
||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.69.151 (0.034 с.) |
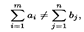

 Математическая модель закрытой транспортной задачи имеет вид:
Математическая модель закрытой транспортной задачи имеет вид:

 На предприятии имеются три группы станков, каждая из которых может выполнять пять операций по обработке деталей (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 110, 130 ч.
На предприятии имеются три группы станков, каждая из которых может выполнять пять операций по обработке деталей (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 110, 130 ч. Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей.
Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей. Находим потенциалы свободных клеток:
Находим потенциалы свободных клеток: Клетка (1;3). -13+0-(-11)=-2 и т.д.
Клетка (1;3). -13+0-(-11)=-2 и т.д.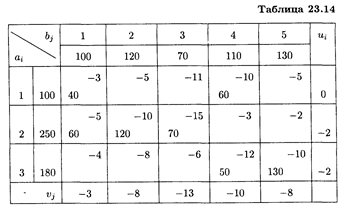
 Так как Δ14 = 3 > 0, перераспределим грузы, получим
Так как Δ14 = 3 > 0, перераспределим грузы, получим

 Решить следующие транспортные задачи, заданные распределительной таблицей.
Решить следующие транспортные задачи, заданные распределительной таблицей.
 5. Требуется спланировать перевозку строительного материала с трех заводов к четырем строительным площадкам, используя железнодорожную сеть. В течение каждого квартала на четырех площадках требуется соответственно 5, 10, 20, 15 вагонов строительных материалов. Возможности различных заводов соответственно равны 10, 15 и 25 вагонов в квартал. Условия задачи даны в табл. 23.15. Числа на пересечении строк и столбцов таблицы означают стоимость перевозки одного вагона (усл. ед.).
5. Требуется спланировать перевозку строительного материала с трех заводов к четырем строительным площадкам, используя железнодорожную сеть. В течение каждого квартала на четырех площадках требуется соответственно 5, 10, 20, 15 вагонов строительных материалов. Возможности различных заводов соответственно равны 10, 15 и 25 вагонов в квартал. Условия задачи даны в табл. 23.15. Числа на пересечении строк и столбцов таблицы означают стоимость перевозки одного вагона (усл. ед.). 7. В трех пунктах производства имеется одинаковая продукция в объеме 200, 170, 130 т. Эта продукция должна быть доставлена потребителям в количестве 50, 220, 80, 110 и 140 т. Стоимости перевозок единицы продукции от каждого поставщика к каждому потребителю заданы матрицей
7. В трех пунктах производства имеется одинаковая продукция в объеме 200, 170, 130 т. Эта продукция должна быть доставлена потребителям в количестве 50, 220, 80, 110 и 140 т. Стоимости перевозок единицы продукции от каждого поставщика к каждому потребителю заданы матрицей 8. Фирма получила заказы на три вида выпускаемой ею продукции (бокалы, чашки и вазы), которые необходимо изготовить в течение следующей недели. Размеры заказов: бокалы — 4000 шт., чашки — 2400 шт., вазы — 1000 шт.
8. Фирма получила заказы на три вида выпускаемой ею продукции (бокалы, чашки и вазы), которые необходимо изготовить в течение следующей недели. Размеры заказов: бокалы — 4000 шт., чашки — 2400 шт., вазы — 1000 шт. На складах A 1, А 2, А 3 имеются запасы продукции в количествах 90, 400, 110 т соответственно. Потребители В 1, В 2, B 3 должны получить эту продукцию в количествах 140, 300, 160 т соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (усл. ед.), см справа.
На складах A 1, А 2, А 3 имеются запасы продукции в количествах 90, 400, 110 т соответственно. Потребители В 1, В 2, B 3 должны получить эту продукцию в количествах 140, 300, 160 т соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (усл. ед.), см справа. Проверим, является ли данная транспортная задача закрытой. Расчет справа.
Проверим, является ли данная транспортная задача закрытой. Расчет справа.
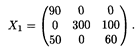 Это значит, что условие невырожденности выполнено. Исходное опорное решение запишем в виде матрицы:Х1
Это значит, что условие невырожденности выполнено. Исходное опорное решение запишем в виде матрицы:Х1



