
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема. Если натуральные числа а, т взаимно просты, то
Следствие. Если р — простое число и
Для доказательства утверждения а) достаточно заметить, что
Заметим, что утверждение а) следствия впервые доказал Ферма, оно называется малой теоремой Ферма. Теорема б была позднее доказана Эйлером и носит название теоремы Эйлера — Ферма. Она находит широкое применение в математике и ее приложениях и, в частности, может оказаться полезной при нахождении остатков от деления степеней числа на заданное число, при решении сравнений с неизвестными и т. д. Кольцо вычетов Рассмотрим множество Следовательно, классы вычетов по модулю та совпадают со смежными классами кольца Z по его идеалу mZ. Теорема 1. Определение операций сложения и умножения классов вычетов по формулам
Кольцо Z/rn называют кольцом классов вычетов по модулю т. Опишем обратимые элементы этого кольца. Теорема 2. Элемент Китайская теорема об остатках Пусть m - натуральное число, m1, m2,..., mt - взаимно простые натуральные числа, произведение которых больше либо равно m. Теорема: Любое число x: 0 <= x <= m может быть однозначно представлено в виде последовательности r(x) = (r1, r2,..., rt), где ri = x(mod mi). Для любых чисел r1.. rt, таким образом, существует единственное число x(mod m), такое что x = ri(mod mi), 1 <= i <= t Более того, любое решение x набора такого сравнений имеет вид x = r1*e1 +... + rt*et (mod m), где ei = m / mi * ((m/mi)-1 mod mi), 1 <= i <= t.
Алгоритмы на графах. Обход графа в глубину, построение глубинного остового леса и классификация ребер, не вошедших в лес. Алгоритмы нахождения связных компонентов неориентированных графов и сильно связных компонентов ориентированных графов. Поиск в ширину и кратчайшие пути в графе. Обход в глубину — это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода): 1) Рассматриваем вершину Х. Двигаемся в любую другую, ранее непосещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой мы впервые попали в данную вершину;
2) Если из вершины Х нельзя попасть в ранее непосещенную вершину или таковой нет, то возвращаемся в вершину Z, из которой впервые попали в X, и продолжаем обход в глубину из вершины Z. 3) Такой обход графа продолжается до тех пор, пока очередная вершина Х, не совпадет с вершиной Х0,с которой начался обход графа (компоненты связности). Обход в ширину — это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода): 1) Рассматриваем вершину Х. Ей присваивается метка 0; 2) Всем смежным вершинам с вершиной с меткой 0 поочередно присваиваются метки 1; 3) Всем смежным вершинам с вершинами с меткой 1 поочередно присваиваются метки 2; 4) И т.д. до тех пор, пока не будут помечены все вершины в текущем графе (компоненте связности). Связный граф Граф, в котором все вершины связаны.
|
|||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.69.255 (0.005 с.) |

 , то
, то
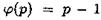 . Утверждение б) при
. Утверждение б) при  следует из а) и следствия 1 теоремы 2, а при
следует из а) и следствия 1 теоремы 2, а при  очевидно, поскольку в этом случае
очевидно, поскольку в этом случае .
.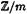 всех классов вычетов по модулю
всех классов вычетов по модулю  . Класс
. Класс  состоит из всех чисел вида
состоит из всех чисел вида  , где t пробегает множество Z, т. е.
, где t пробегает множество Z, т. е. 
 корректно, и множество
корректно, и множество  с этими операциями является коммутативным кольцом с единицей. Это есть факторкольцо
с этими операциями является коммутативным кольцом с единицей. Это есть факторкольцо  кольца Z по его идеалу тZ.
кольца Z по его идеалу тZ. обратим в кольце Z/m тогда и только тогда, когда класс
обратим в кольце Z/m тогда и только тогда, когда класс 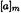 взаимно прост с т, т. е. (а,т) = 1.
взаимно прост с т, т. е. (а,т) = 1.


