
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нечіткі множини. Операції над нечіткими множинами та їх властивості
Мабуть, найбільш вражаючим у людському інтелекті є здатність приймати правильні рішення в умовах неповної й нечіткої інформації. Побудова моделей наближених роздумів людини і використання їх у комп’ютерних системах є на сьогодні однією із найважливіших проблем науки. Основи нечіткої логіки були закладені у кінці 60-их роках у роботах відомого американського математика Лафти Заде. Дослідження були пов’язані з наростаючим невдоволенням експертними системами. Хвалений “штучний інтелект”, який легко справлявся із задачами управління складних технічних комплексів, був безпорадний при найпростіших висловленнях повсякденного життя, наприклад, “Якщо в машині перед тобою сидить недосвідчений водій — тримайся від нього подалі”. Для створення дійсно інтелектуальних систем, здатних адекватно взаємодіяти з людиною, був необхідний новий математичний апарат, який би перекладав неоднозначні життєві твердження мовою чітких та формальних математичних формул. Першим серйозним кроком у цьому напрямі стала теорія нечітких множин, розроблена Заде. Його робота “Fuzzy Sets”, опублікована у 1965 році у журналі “Information and Control”, заклала основи моделювання інтелектуальної діяльності людини й стала початковим поштовхом до розвитку нової математичної теорії. Він же і дав назву цій новій галузі науки – “fuzzy logic” (fuzzy – нечіткий, розмитий, м’який). Подальші роботи професора Латфи Заде та його послідовників заклали фундамент для впровадження методів нечіткого управління в інженерну практику. Апарат теорії нечітких множин, продемонструвавши низку багатообіцяних можливостей застосування – від систем управління літальними апаратами до прогнозування підсумків виборів, виявився разом з тим складним для втілення. Враховуючи наявний рівень технології, нечітка логіка зайняла своїє місце серед інших спеціальних наукових дисциплін – посередині між експертними системами й нейронними мережами. Своє друге народження теорія нечіткої логіки пережила на початку 80-их років, коли декілька груп дослідників (США і Японії) серйозно зайнялися створенням електронних систем різного застосування, використовуючи нечіткі управляючі алгоритми. Теоретичні основи для цього були закладені у ранніх роботах Коско та інших вчених.
Третій період почався з кінця 80-их років і до цього часу. Цей період характеризується бумом практичного застосування теорії нечіткої логіки у різних сферах науки та техніки. До 90-го року з’явилося біля 40 патентів, що належали до нечіткої логіки (30 – японських). 48 японських компаній створюють лабораторію LIFE (Laboratory for International Fuzzy Engineering), японський уряд фінансує 5-річну програму з нечіткої логіки, яка включає 19 проектів – від системи оцінки глобального забруднення атмосфери і передбачення землетрусів до АСУ заводських цехів. Результатом виконання цієї програми була поява нових масових мікрочіпів, що базувалися на нечіткій логіці. Сьогодні їх можна знайти у пральних машинах та відеокамерах, цехах заводів і у моторах автомобілів, у системах управління складськими роботами й бойовими гелікоптерами. У США розвиток нечіткої логіки йде по шляху створення системи для великого бізнесу і військових. Нечітка логіка застосовується в аналізі нових ринків, біржевій грі, оцінці політичних рейтингів, виборі оптимальної цінової стратегії та ін. З’явилися і комерційні системи масового застосування. Це привело до низки проблем, а саме: § нові архітектури комп’ютерів для нечітких обчислювань; § елементна база нечітких комп’ютерів та контролерів; § інструментальні засоби розробки; § інженерні методи розрахунку й розроблення нечітких систем управління і т.д. Нехай Е є множина, А – підмножина Е:
Приклад. Розглянемо скінченну множину з 5 елементів
та Запишемо для кожного елемента із Е степінь його належності множині А
Це дозволяє представити А через всі елементи множини У, супроводжуючи кожний з них значенням його функції належності:
Отже, нехай
Нечітка підмножина відрізняється від звичайної тим, що для елементів Функція належності вказує степінь (або рівень) належності елемента Строге визначення поняття нечіткої множини, введене Заде. Нехай Е є множина, скнченна або ні, й x – елемент Е. Тоді нечіткою підмножиною А множини Е називається множина впорядкованих пар Таким чином, якщо Приклад Нечітка підмножина чисел x, приблизно рівних даному дійсному числові n, де Розглянемо множину
Покажемо функцію належності множини
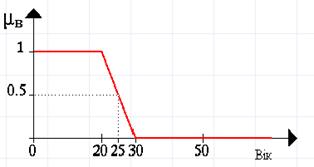
Рис. 1.5.1. Графічне зображення результату функції належності Можна інтерпретувати елементи, що відповідають 1 як елементи, котрі знаходяться у множині У цьому прикладі опишемо множину людей. Формально це можна записати так: Оскільки, взагалі, вік починається з 0, то нижня границя цієї множини повинна бути нулем. Верхню границю визначити складніше. Спочатку встановимо верхню границю, наприклад, рівну 20 рокам. Таким чином, маємо В як чітко визначений інтервал, буквально Більш природний шлях створення множини В полягає в послабленні строгого поділу на молодих і на немолодих. Зробимо це, формулюючи не тільки чіткі судження “Так, він належить множині молодих людей” або “Ні, вона не належить множині молодих людей”, але й гнучкі формулювання, наприклад: “Так, належить множині доволі молодих людей”, “Ні, він не дуже старий”. Розглянемо, як за допомогою нечіткої множини визначити вираз “Він ще молодий”. У першому прикладі ми кодували всі елементи множини за допомогою 0 або 1. Простим способом узагальнити цю концепцію є введення значень між 0 та 1. Реально можна навіть допустити нескінченне число значень між 0 та 1, в одиничному інтервалі Інтерпретація чисел при співвідношенні всіх елементів множини стає тепер складнішою. Звичайно, число 1 відповідає елементу, що належить множині В, а 0 означає, що елемент точно не належить множині В. Усі інші значення визначають степінь належності до множини В. Для наочності покажемо характеристичну функцію множини молодих людей, як і в першому прикладі (рис. 1.5.2).
Рис. 1.5.2. Характеристична функція Нехай E = {x1, x2, x3, x4, x5 }, M = [0,1]; A – нечітка множина, для якої
Тоді A можна представити у вигляді: A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } або A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5 (знак “+” є операцією не додавання, а об’єднання) або
|
|||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 763; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.195.121 (0.019 с.) |
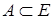 . Той факт, що елемент
. Той факт, що елемент 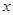 належить множині А позначають
належить множині А позначають 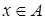 . Для вираження цієї належності можна використати й інше поняття – характеристичну функцію –
. Для вираження цієї належності можна використати й інше поняття – характеристичну функцію – 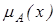 , значення якої вказує, чи
, значення якої вказує, чи  належить множині А.
належить множині А.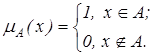
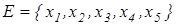
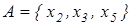 .
.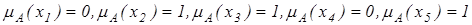 .
.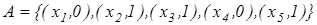 .
. – універсальна множина,
– універсальна множина, 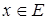 , а
, а  – деяка властивість. Звичайна (чітка) підмножина
– деяка властивість. Звичайна (чітка) підмножина  універсальної множини
універсальної множини 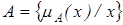 , де
, де  (наприклад,
(наприклад, 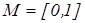 – на інтервалі).
– на інтервалі).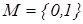 , тоді нечітка підмножина
, тоді нечітка підмножина  може розглядатись як звичайна або чітка множина.
може розглядатись як звичайна або чітка множина.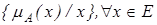 , де
, де 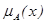 – ступінь належності x в А.
– ступінь належності x в А.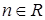 (
( усіх чисел від 0 до 10. Визначимо підмножину
усіх чисел від 0 до 10. Визначимо підмножину  усіх дійсних чисел від 5 до 8, коли
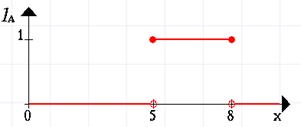
усіх дійсних чисел від 5 до 8, коли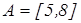 .
.
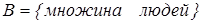 .
.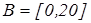 . Виникає питання: чому хтось у свій двадцятилітній юбілей – молодий, а зразу на наступний день уже не молодий? Очевидно, це структурна проблема, і якщо пересунути верхню границю в іншу точку, то можна задавати таке саме запитання.
. Виникає питання: чому хтось у свій двадцятилітній юбілей – молодий, а зразу на наступний день уже не молодий? Очевидно, це структурна проблема, і якщо пересунути верхню границю в іншу точку, то можна задавати таке саме запитання.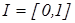 .
.
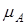 (x1)=0,3;
(x1)=0,3; 


