
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства постоянной функции.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте I. Теоретическая часть. 1. Функция. Определения и свойства. Линейной функцией называется функция вида Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками. Свойства линейной функции 1. Область определения - множество всех действительных чисел: Д(y)=R 2. Множество значений - множество всех действительных чисел: Е(у)=R 3. Функция принимает нулевое значение при 4. Функция возрастает (убывает) на всей области определения. 5. Линейная функция непрерывная на всей области определения, дифференцируемая и Квадратичная функция. Функция вида Коэффициенты а, b, с определяют расположение графика на координатной плоскости Коэффициент а определяет направление ветвей. График квадратичной функции - парабола. Координаты вершины параболы находятся по формулам:
Свойства функции: 1. D(у)=R. 2. Множество значений одного из промежутков: 3. Функция принимает нулевые значения при 4. Функция непрерывна на всей области определения и производная функции равна Показательная функция. Функция вида Коэффициент а - положительное число, указывает на возрастание или убывание функции. Свойства функции: 1. Д(у)=R. 2. Е(у)= 3. Функция возрастает (а>1), убывает (а<1) на всей области определения. 4. График функции пересекает ось ординат в точке (0;1). 5. Функция непрерывна на всей области определения, дифференцируема и производная равна Логарифмическая функция Логарифмической функцией называется функция вида Число а определяет расположение графика. Вместо логарифмической функции с произвольным основанием удобно рассматривать функцию вида Так как Свойства функции у=ln x. 1. Д(у)= 2. Е(у)=R. 3. Функция принимает нулевое значение при х=1. 4. Функция возрастает на всей области определения. 5. Функция является непрерывной на всей области определения, дифференцируема и Степенная функция Степенной функцией с действительным показателем называется функция вида Примеры степенных функций: Коэффициент b определяет положение графика на координатной плоскости. Свойства функции. 1. Функция определена для х>0. 2. Е(у)= 3. Функция возрастающая, если b>0 и убывающая, если b<0. 4. Функция непрерывна на всей области определения, дифференцируемая и
2. Основные элементарные функции. Определения, формулы, свойства, графики. Постоянная функция. Постоянная функция задается на множестве всех действительных чисел формулой Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5, y=-2 и
Степенная функция. Степенная функция задается формулой вида Рассмотрим вид графиков степенной функции и свойства степенной функции в зависимости от значения показателя степени. Начнем со степенной функции с целым показателем a. В этом случае вид графиков степенных функций и свойства функций зависят от четности или нечетности показателя степени, а также от его знака. Поэтому сначала рассмотрим степенные функции Свойства степенных функций с дробными и иррациональными показателями (как и вид графиков таких степенных функций) зависят от значения показателя a. Их будем рассматривать, во-первых, при a от нуля до единицы, во-вторых, при a больших единицы, в-третьих, при a от минус единицы до нуля, в-четвертых, при a меньших минус единицы. В заключении этого пункта для полноты картины опишем степенную функцию с нулевым показателем.
3. Построение графиков элементарных функций.
1. Об элементарных приемах построения графиков: а) приемы, связанные с применением геометрических преобразований плоскости (параллельный перенос, симметрия, деформация);б) приемы построения графиков кусочных функции, т.е. функций, заданных различными формулами на разных участках области определения, например, функция: Рекомендуем предварительно повторить теоретический материал, связанный с указанными знаниями, затем разобрать примеры, приведенные в данном параграфе, и только после этого приступить к выполнению предложенных упражнений. Переменная величина y называется функцией переменной величины x, если каждому значению x соответствует определенное значение y. Множество всех тех значений, которые принимает аргумент x функции y = f (x), называется областью определения этой функции. Множество всех тех значений, которые принимает сама функция y = f (x), называется областью значений (изменения) этой функции. Функция y = f (x) называется четной, если при всех значений x из области определения этой функции f (-x) = f (x). Функция y = f (x) называется нечетной, если при всех значений x из области определения этой функции f (-x) = -f (x). Область определения четной и нечетной функции симметрична относительно начала координат. Функция y = f (x) называется возрастающей (убывающей) на данном промежутке, если при произвольных двух различных значениях аргумента из данного промежутка большему значению аргумента соответствует большее (меньшее) значение функции.Функция y = f (x) называется периодической, с периодом T, где T ≠ 0, если значение функции не изменяется при прибавлении числа T к любому допустимому значению аргумента: f (x+T) = f (x). Функция y = f (x) называется ограниченной, если можно указать такое положительное число M, что |f (x)| ≤ M для всех значений x из области определения функции. Если же точка M не существует, то функция называется неограниченной. Графиком функции y = f (x) называется множество всех точек плоскости, координаты которых (x, f (x)). Функцию вида y = ax2 + bx + c называют квадратичной. Графиком квадратичной функции является кривая, называемая параболой. Точку с координатами 1) множество X (которое называется областью определения функции);2) множество Y (которое называется областью значений функции);3) закон соответствия (который иногда называется функциональной зависимостью). При этом закон соответствия может быть задан любым способом: таблицей, графиком, формулой или как-то иначе, например, при помощи словесного описания. Если функцию задают формулой, то при этом фактически указывают область определения функции и закон соответствия (область значений функции не указывается явно, так как она устанавливается исходя из данной формулы).Областью определения функции, заданной явной аналитической формулой, считают множество всех тех значений аргумента, для которых все указанные в формуле операции выполнимы.
способы построения графиков функций. 1. Способ «по точкам». Вытекает из определения графика функции. Он является длинным и недостаточно надежным. Применяется в школьном курсе математики при первоначальном знакомстве с простейшими функциями. 2. Способ «путем сдвига графиков основных функций или сдвига осей координат». Чтобы построить график функции y = f (x) + c можно или график функции y = f (x) сдвинуть вдоль оси 0y на c единиц в сторону, совпадающую со знаком c, или перенести параллельно ось 0y в сторону, противоположную знаку c. Чтобы построить график функции y = f (x + b), можно или график функции y = f (x) вдоль оси 0x на b единиц в сторону, противоположную знаку b, или перенести параллельно ось 0y в сторону, совпадающую со знаком b. 3. Способ «путем симметричного отображения относительно осей координат». Чтобы построить график функции y = -f (x), можно построить изображение, симметричное графику функции y = f (x) относительно оси абсцисс. Чтобы построить график функции y = f (-x), можно построить изображение, симметричное графику функции y = f (x) относительно оси ординат. 4. Способ «путем деформирования графиков основных функций». Чтобы построить график функции y = af (x) при a > 0, можно график исходной функции растянуть (сжать) вдоль оси ординат, если a > 1 (0 < a < 1).Чтобы построить график функции y = f (b ∙ x) при b > 0, можно график исходной функции растянуть (сжать) вдоль оси абсцисс, если b > 1 (0 < b < 1).
4. Предел числовой последовательности.
Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, число Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел. Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые ирациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений.[1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей. Определение Число
В случае, если у числовой последовательности существует предел в виде вещественного числа
Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.
Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.
Можно дать альтернативные определения предела последовательности. Например, называть пределом число, в любой окрестности которого содержится бесконечно много элементов последовательности, в то время, как вне таких окрестностей содержится лишь конечное число элементов. Таким образом, пределом последовательности может быть только предельная точка множества её элементов. Это определение согласуется с общим определением предела для топологических пространств. Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из доказываемых ниже свойств предела.
5. Предел функции в точке и в бесконечности.
Рассмотрим функцию Существуют два определения Предела функции в точке. Определение Число Для обозначения предельного значения функции используется следующая символика: Отметим, что функция Рассмотрим несколько Примеров. 1. Функция
2. Функция
Соответствующие последовательности значений функций для них:
Таким образом, Определение 1 не удовлетворяется, так как для двух разных последовательностей значений аргумента, сходящихся к нулю, соответствующие последовательности значений функции имеют разные пределы.
6. Бесконечно малые функции и их свойства.
Если Свойства 1. Сумма (разность) конечного числа бесконечно малых функций при Доказательство 2. Произведение бесконечно малой функции Доказательство 3. Произведение конечного числа бесконечно малых функций при Доказательство
7. Основные теоремы о пределах функции.
Определение. Число A называется пределом функции y = f (x) в точке x 0(иногда говорят, при x, стремящемся к x 0), если для любого положительного числа e можно найти такое положительное число d, что для всех x из d - окрестности точки x 0соответствующие значения y попадают в e - окрестность точки y = A. Можно сформулировать определение предела функции по-другому. Определение. Число A называется пределом функции y = f (x) в точке x 0, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию 0 < ê x - x 0ê < d, выполняется условие ê y - A ê < e. Тот факт, что A есть предел функции y = f (x) в точке x = x 0, записывается формулой
Свойства предела функции 1. Функция не может иметь в одной точке два разных предела. 2. 3. Если существует
4. Если существуют Примеры 1. 2. 3.
8. Первый и второй замечательные пределы, их следствия.
Следствия первого замечательного предела запишем формулами Таблица простейших неопределённых интегралов 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Формулы (2.7) – (2.16) простейших неопределённых интегралов следует выучить наизусть. Знание их необходимо, но далеко не достаточно для того, чтобы научиться интегрировать. Устойчивые навыки в интегрировании достигаются только решением достаточно большого числа задач (обычно порядка 150 – 200 примеров различных типов).
37. Рациональные дроби. Основные понятия. Разложение рациональной дроби на простейшие.
Торема Правильную рациональную дробь
где Без доказательства. Согласно данному разложению, линейным множителям знаменателя Пример. Разложить на элементарные дроби Решение. Выделим из неправильной дроби целую часть, деля числитель на знаменатель
Разложим полученную в результате дробь на элементарные слагаемые:
Тогда Для нахождения коэффициентов разложения, чаще всего используется метод неопределенных коэффициентов и метод частных значений. Метод неопределенных коэффициентов.Суть метода неопределенных коэффициентов состоит в следующем. ▪ Раскладываем правильную рациональную дробь ▪ Простейшие дроби приводим к общему знаменателю ▪ Многочлен, получившийся в числителе, приравниваем к многочлену ▪ Для тождественного равенства двух многочленов необходимо и достаточно, чтобы коэффициенты при одинаковых степенях
38. Интегрирование простейших рациональных дробей.
Определение: Элементарными называются дроби следующих четырех типов: I. II. m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0. Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b. I. II. Рассмотрим метод интегрирования элементарных дробей вида III. Интеграл дроби вида III может быть представлен в виде:
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам
39. Интегрирование тригонометрических выражений.
Рациональные функции. Условимся через Интегралы вида Будем рассматривать интегралы вида Заметим, что в интегральном исчислении нет общих правил. Интегрирование может быть выполнено не единственным способом. Но даже и тогда, когда имеется теоретическое правило вычисления интеграла, оно может оказаться далеко не лучшим. Для вычисления интегралов вида Действительно, пусть
Подставляя в подынтегральное выражение вместо
Подынтегральная функция рациональна относительно |
|
| Поделиться: |

 , где х - переменная, а и b - действительные числа.
, где х - переменная, а и b - действительные числа. или
или  .
. .
. , где х - переменная, коэффициенты а, b, с - действительные числа
, где х - переменная, коэффициенты а, b, с - действительные числа  , называется квадратичной.
, называется квадратичной.
 или
или 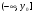 .
. , где дискриминант вычисляется по формуле:
, где дискриминант вычисляется по формуле:  .
. .
.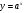 , где
, где  называется показательной функцией.
называется показательной функцией. .
. .
.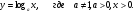
 .
.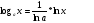 , то указанные функции исчерпывают все логарифмические функции.
, то указанные функции исчерпывают все логарифмические функции.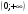 .
. .
. , где b-действительное число, х>0.
, где b-действительное число, х>0. .
. .
. .
.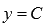 , где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
, где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой. , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
, которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.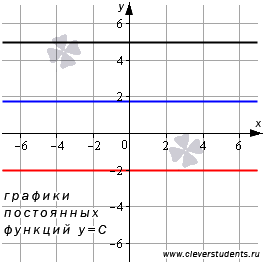
 .
. в) приемы так называемого «сложения» графиков функций.
в) приемы так называемого «сложения» графиков функций. называют вершиной параболы. Соответствие между элементами двух множеств X и Y, при котором каждому элементу множества X сопоставляется не более одного элемента Y, называется функцией. Отсюда следует, что понятие функции имеет три главных компонента:
называют вершиной параболы. Соответствие между элементами двух множеств X и Y, при котором каждому элементу множества X сопоставляется не более одного элемента Y, называется функцией. Отсюда следует, что понятие функции имеет три главных компонента: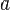 называется пределом последовательности
называется пределом последовательности , если для любого
, если для любого  существует номер
существует номер  , зависящий от
, зависящий от 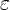 такой, что для любого
такой, что для любого  выполняется неравенство
выполняется неравенство  .
. называется пределом числовой последовательности
называется пределом числовой последовательности  является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.



 , определенную на некотором множестве
, определенную на некотором множестве 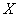 и точку
и точку  , быть может, и не принадлежащую множеству
, быть может, и не принадлежащую множеству  –окрестности точки
–окрестности точки  , отличные от
, отличные от  .
. называется Предельным значением функции
называется Предельным значением функции 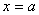 (или Пределом функции при X® A), если для любой сходящейся к А Последовательности
(или Пределом функции при X® A), если для любой сходящейся к А Последовательности 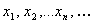 значений аргумента
значений аргумента  , элементы
, элементы  которой отличны от
которой отличны от  .
. может иметь только один предел.
может иметь только один предел.
 Имеет в точке
Имеет в точке  предел, равный –2. Действительно, пусть
предел, равный –2. Действительно, пусть  – любая последовательность значений аргумента, сходящаяся к нулю, т. е.
– любая последовательность значений аргумента, сходящаяся к нулю, т. е.  , тогда при
, тогда при  в силу теорем о свойствах сходящихся последовательностей:
в силу теорем о свойствах сходящихся последовательностей: .
. определена для всех
определена для всех  . В точке
. В точке  и
и  .
. .
. , то функция
, то функция  называется бесконечно малой при
называется бесконечно малой при  .
. бесконечно малые функции при
бесконечно малые функции при  и число
и число  такие что
такие что (1)
(1)  (2).
(2).  , то условие
, то условие 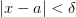 усиливает группу условий (1) что влечет за собой группу условий (2). Следовательно
усиливает группу условий (1) что влечет за собой группу условий (2). Следовательно в некоторой проколотой окрестности точки
в некоторой проколотой окрестности точки  есть бесконечно малая функция при
есть бесконечно малая функция при  удовлетворяющих условию
удовлетворяющих условию (1)
(1)  (2)
(2)  и число
и число (3)
(3)  (4)
(4) 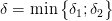 . Тогда условие
. Тогда условие 
 окрестности точки
окрестности точки  .
.
 , если C - постоянная функция.
, если C - постоянная функция. и C - постоянная функция, то
и C - постоянная функция, то .
. и
и  , то существует
, то существует  , равный
, равный  , а также существует
, а также существует  , равный
, равный 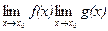 . Если при этом
. Если при этом  , то существует
, то существует  , равный
, равный  .
. 3-2+7=8.
3-2+7=8.
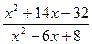
 (применить четвертое свойство (для частного) нельзя, т.к. предел знаменателя при x
(применить четвертое свойство (для частного) нельзя, т.к. предел знаменателя при x 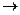 2 равен нулю; в таких случаях говорят, что имеем неопределенность вида
2 равен нулю; в таких случаях говорят, что имеем неопределенность вида  ; для ее раскрытия раскладываем числитель и знаменатель дроби на множители) =
; для ее раскрытия раскладываем числитель и знаменатель дроби на множители) = 

 . Аналогичный приём вычисления пределов можно использовать для раскрытия неопределенностей в случае иррациональных функций.
. Аналогичный приём вычисления пределов можно использовать для раскрытия неопределенностей в случае иррациональных функций.

 =(в числители разность квадратов)
=(в числители разность квадратов)  =
=  =
=  = -
= -  =
=  .
.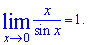 2.
2.  3.
3.  4.
4. 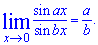 Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль
Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль  для выражений с тригонометрическими функциями.
для выражений с тригонометрическими функциями. , где
, где 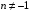 , (2.7)
, (2.7)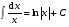 , где
, где  , (2.8)
, (2.8)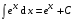 , (2.9)
, (2.9) , где
, где  ,
,  , (2.10)
, (2.10) , (2.11)
, (2.11) , (2.12)
, (2.12) , (2.13)
, (2.13) , (2.14)
, (2.14) , (2.15)
, (2.15) . (2.16)
. (2.16) , где
, где  , можно единственным образом разложить на сумму простейших дробей:
, можно единственным образом разложить на сумму простейших дробей:

 ,
, ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  – некоторые действительные числа.
– некоторые действительные числа. соответствуют простейшие дроби первого и второго типов, а квадратным множителям – третьего и четвертого типов. При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя дроби. Формула разложения правильной рациональной дроби на простейшие дроби остается справедливой для любого конечного числа линейных и квадратных множителей, входящих в разложение знаменателя
соответствуют простейшие дроби первого и второго типов, а квадратным множителям – третьего и четвертого типов. При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя дроби. Формула разложения правильной рациональной дроби на простейшие дроби остается справедливой для любого конечного числа линейных и квадратных множителей, входящих в разложение знаменателя 
 .
. .
. .
. .
. этих многочленов были равны. Учитывая это, приравниваем коэффициенты при одинаковых степенях
этих многочленов были равны. Учитывая это, приравниваем коэффициенты при одинаковых степенях  линейных алгебраических уравнений для нахождения
линейных алгебраических уравнений для нахождения  ,
, 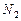 , ….,
, ….,  III.
III. 
 IV.
IV. 


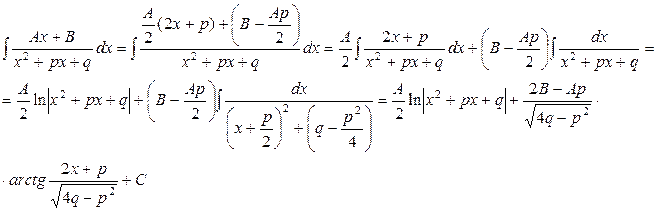
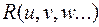 обозначать рациональную функцию относительно
обозначать рациональную функцию относительно  ,
,  ,
,  ,..., т. е. выражение, которое получено из любых величин
,..., т. е. выражение, которое получено из любых величин  . Универсальная подстановка.
. Универсальная подстановка. . Этой подстановкой интеграл
. Этой подстановкой интеграл  , который, как было показано, всегда выражается в элементарных функциях.
, который, как было показано, всегда выражается в элементарных функциях. ,
,  и
и  через
через 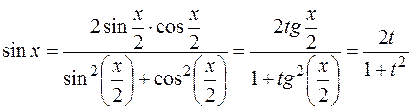 ,
, ,
, ,
,  .
. ,
,  .
.


