
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА 3.2. Уравнение Бернулли
• Выделим в потоке столь тонкую трубку тока и выберем промежуток времени Δ t столь малый, чтобы всем точкам каждого из малых объёмов Δ W 1и Δ W 2можно было приписать одинаковые значения площади живого сечения, скорости, давления и высоты, а именно: ω 1, u 1, p 1, z 1 для Δ W 1и ω 2, u 2, p 2, z 2 для Δ W 2. Объём Δ W 1 = ω 1 u 1Δ t – это объём между сечением ω 1 и сечением
Поскольку сечения взяты произвольно, то, разделив уравнение на ρ Δ Wg, получим уравнение Бернулли для трубки тока:
гравитационную потенциальную энергию
называемую также гравитационным напором или напором положения. • Второе слагаемое в уравнении (3.2.2) представляет собой удельную (приходящуюся на единицу веса) потенциальную энергию давления, называемую также напором давления. • Третье слагаемое в уравнении (3.2.2) представляет собой удельную (приходящуюся на единицу веса) кинетическую энергию
называемую также скоростным напором. • Суммарный потенциальный напор z + p/γ называется пьезометрическим напором, так как он равен отметке жидкости в пьезометре (см. рис. 2.2.1). • Сумма пьезометрического и скоростного напора
называется полным или гидродинамическим напором. • Уравнение Бернулли является следствием закона сохранения энергии: полный напор H 0, т.е. сумма геометрического напора z и напора давления p/γ, а также скоростного напора (удельной кинетической энергии) u 2/(2 g) идеальной жидкости (несжимаемой жидкости, в которой вязкостью можно пренебречь) есть величина постоянная для разных живых сечений трубки тока:
• Геометрическая трактовка уравнения Бернулли: полный напор H 0, т.е. сумма геометрической отметки z, пьезометрической высоты p/γ и высоты скоростного напора u 2/(2 g) есть величина постоянная для разных живых сечений.
• Гидродинамическая трубка (трубка Пито) погружается в поток жидкости загнутым концом навстречу течению (рис. 3.2.2). Разность уровней жидкости в гидродинамической трубке и в пьезометре равняется скоростному напору • Уравнение Бернулли для реальной жидкости отличается наличием слагаемого h, которое представляет собой потери напора (удельной энергии) на длине l между сечениями:
Линия 3 на рис. 3.2.2 является линией плоскости сравнения. • Линия 2 на рис. 3.2.2, которая соединяет отметки пьезометров, называется пьезометрической линией, или линией удельной потенциальной энергии, а её уклон пьезометрическим уклоном:
• Линия 1 на рис. 3.2.2, которая соединяет отметки гидродинамических напоров (отметки гидродинамических трубок), называется напорной линией, или линией суммарной удельной энергии, а ее уклон гидравлическим уклоном:
• Установившееся движение – это такое движение, при котором скорость и давление в отдельных точках пространства, через которое перетекает жидкость, не изменяется со временем. Установившееся движение может быть равномерным и неравномерным. • Призматическое русло – это такое русло, форма и размеры которого по длине потока остаются неизменными. • Равномерное движение – это такое движение, при котором скорость, давление и распределение их по сечению при постоянной форме и размерах живого сечения не изменяются вдоль пути жидкости (примеры: течение воды в круглой трубе или в призматическом канале при постоянной глубине h). • Основное уравнение равномерного движения жидкости: пьезометрический уклон
где • Плавноизменяющееся движение – это движение, при котором линии тока параллельны или почти параллельны, а кривизна струек незначительна. Следовательно, ускорением можно пренебречь. Уравнение Эйлера для вертикального направления
принимает вид:
Интегрируя это уравнение, получаем:
В горизонтальной плоскости p = const. (3.2.14) • Уравнение равномерного движения жидкости: вследствие постоянства скорости напорная линия параллельна пьезометрической, и гидравлический уклон равняется пьезометрическому:
• Уравнение равномерного движения в открытых руслах: пьезометрический уклон ip равняется уклону i поверхности потока и дна русла, а также гидравлическому уклону J: i = ip = J. (3.2.16) • Масса, прошедшая через сечение струйки за единицу времени, dm = ρudω. Энергия, переносимая потоком за единицу времени,
где α – корректив кинетической энергии (коэффициент Кориолиса), который представляет собой отношение действительной кинетической энергии к кинетической энергии, подсчитанной по средней скорости, и отражает неравномерность распределения скоростей по сечению:
Для ламинарного течения α = 2, для турбулентного α = 1,1. • В отсутствие внутреннего трения через любое сечение при равномерном или плавноизменяющемся движении за единицу времени переносится одинаковая энергия
• Отсюда следует уравнение Бернулли для равномерного или плавноизменяющегося движения:
Гидродинамический напор в любом сечении плавноизменяющегося потока идеальной жидкости есть величина постоянная. • Условия плавноизменяющегося движения должны выполняться вблизи рассматриваемых сечений, между которыми движение может и не быть плавноизменяющимся:
• Уравнение Бернулли для двух сечений реальной жидкости:
где h 12 – потери напора между сечениями 1 и 2.
Пример 3.2.1. Гидродинамическая трубка (трубка Пито) помещена в потоке жидкости изогнутым концом вдоль оси трубы против течения и работает в комплексе с обычным пьезометром (рис. 3.2.3). Разность уровней воды в трубке Пито и в пьезометре h = 25 мм. Чему равна скорость потока на оси трубы? Решение. Уравнение Бернулли для сечений 1-1 перед входом в трубку Пито и 2-2 на поверхности воды в пьезометре: Скорость потока на оси трубы
Пример 3.2.2. Определить расход воды Q в трубе диаметром D 1 = 250 мм, имеющей плавное сужение до диаметра D 2 = 125 мм, если показания пьезометров: h 1 = 50 см; в сужении h 2 = 30 см (рис. 3.2.4). Решение. Перепад пьезометрического напора: Площади сечений:
Далее
Расход
Пример 3.2.3. Определить, на какую высоту поднимается вода в трубке, один конец которой присоединён к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды Q = 25 л/с, показание пьезометра перед сужением h 1 = 5 м, диаметры d 1 = 100 мм и d 2 = 50 мм (рис. 3.2.5). Решение. Из уравнения Бернулли при коррективе кинетической энергии
Учитывая, что
Полученная отрицательная высота – вакуумметрическая высота. На эту высоту h вак = 2,7 м и поднимется вода в трубке.
Ньютон – Эйлер – Бернулли
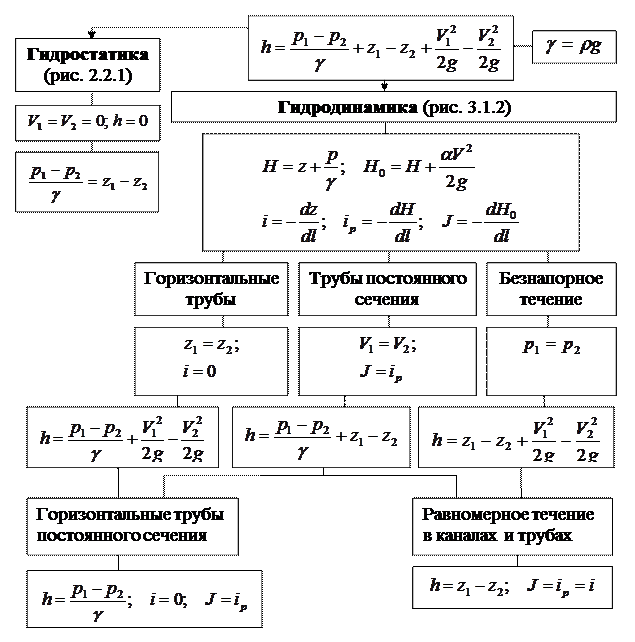
Рис. 3.2.6. Связь законов Ньютона, Эйлера и Бернулли.
Рис. 3.2.7. Схема к уравнению Бернулли. ТЕМА 3.3. Импульс жидкости • Импульс жидкости, протекающей за единицу времени через поперечное сечение элементарной струйки, dK = ρudω · u = ρu 2 dω. (3.3.1) Выражая местную скорость u через среднюю V формулой u = V + ε, найдём импульс жидкости, протекающей за единицу времени через поперечное сечение потока:
Второе слагаемое равно нулю:
Получаем
Выражение в скобках называется коррективом импульса или коэффициентом Буссинеска α 0. • Тогда импульс жидкости, протекающей за единицу времени через поперечное сечение потока, K = α 0 ρV 2 ω = α 0 ρQV. (3.3.2) • Таким образом, корректив импульса есть отношение импульса, рассчитанного по местным скоростям, к импульсу, рассчитанному по средней скорости потока: α 0 = K/ (ρQV). (3.3.3) • При обтекании углов за ними возникают водоворотные зоны, на поддержание течений в которых расходуется энергия. При резком расширении горизонтальной трубы (рис. 3.3.1) из уравнения Бернулли для сечений 1-1 и 2-2 потеря напора h = (p 1 – p 2)/ γ + α (V 12 – V 22)/(2 g). Изменение импульса жидкости, протекающей за единицу времени через поперечное сечение потока, равно сумме сил, действующих на объём жидкости между сечениями, α 0 ρQ (V 2 – V 1) = p 1 ω 2 – p 2 ω 2, Так как α 0 ≈ α, то p 1 – p 2 ≈ αρV 2(V 2 – V 1). Потеря напора
Получена Формула Вейсбаха
где ζ – коэффициент местного сопротивления, для резкого расширения трубы даваемый формулой Бордá:
Пример 3.3.1. Горизонтальная труба диаметром D 1 = 0,10 м внезапно переходит в трубу диаметром D 2 = 0,15 м. Проходящий расход воды Q = 0,03 м3/с. Определить потери напора h при внезапном расширении трубы и разность давлений Δ p в обеих трубах.
Решение. Коэффициент местного сопротивления
Площади сечений труб:
Скорости:
Потери напора
Из уравнения Бернулли разность давлений
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 1375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.98 (0.055 с.) |
 , в которое переместятся частички жидкости, первоначально пребывавшие в сечении ω 1. Объём Δ W 2 = ω 2 u 2Δ t. Из уравнения неразрывности ω 1 u 1 = ω 2 u 2 следует: Δ W 1 = Δ W 2 = Δ W. Таким образом, через время Δ t объём жидкости, пребывавшей вначале между сечениями ω 1 и ω 2, окажется между сечениями
, в которое переместятся частички жидкости, первоначально пребывавшие в сечении ω 1. Объём Δ W 2 = ω 2 u 2Δ t. Из уравнения неразрывности ω 1 u 1 = ω 2 u 2 следует: Δ W 1 = Δ W 2 = Δ W. Таким образом, через время Δ t объём жидкости, пребывавшей вначале между сечениями ω 1 и ω 2, окажется между сечениями  . Изменение энергии этого объёма равно работе сил давления:
. Изменение энергии этого объёма равно работе сил давления: . (3.2.1)
. (3.2.1) . (3.2.2)
. (3.2.2)
 , (3.2.3)
, (3.2.3) , (3.2.4)
, (3.2.4) (3.2.5)
(3.2.5) .
. . (3.2.7)
. (3.2.7) . (3.2.8)
. (3.2.8) . (3.2.9)
. (3.2.9)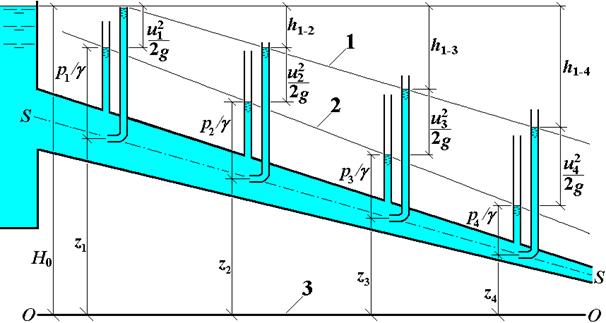
 , (3.2.10)
, (3.2.10) – касательное напряжение на поверхности соприкосновения потока с руслом.
– касательное напряжение на поверхности соприкосновения потока с руслом.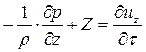 (3.2.11)
(3.2.11) . (3.2.12)
. (3.2.12) . (3.2.13)
. (3.2.13)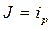 . (3.2.15)
. (3.2.15) ;
;  ,
, . (3.2.17)
. (3.2.17) . (3.2.18)
. (3.2.18) . (3.2.19)
. (3.2.19) . (3.2.20)
. (3.2.20)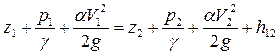 , (3.2.21)
, (3.2.21)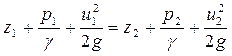 . Уравнение записывается для элементарной струйки, поэтому
. Уравнение записывается для элементарной струйки, поэтому  и
и  – местные скорости. В данном случае
– местные скорости. В данном случае  ;
;  ;
;  ; манометрическое давление на поверхности жидкости в трубке Пито
; манометрическое давление на поверхности жидкости в трубке Пито  . Тогда
. Тогда  . Скоростной напор на входе трубки Пито
. Скоростной напор на входе трубки Пито  .
. 0,700 м/с.
0,700 м/с. . Из уравнения Бернулли при
. Из уравнения Бернулли при  и в пренебрежении потерями напора
и в пренебрежении потерями напора  получаем
получаем  . Из уравнения неразрывности
. Из уравнения неразрывности  имеем
имеем  .
. 0,0491 м2;
0,0491 м2; 0,0123 м2.
0,0123 м2. ;
; 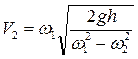 . Расход
. Расход 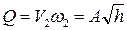 , где
, где 0,0563 м2,5/с.
0,0563 м2,5/с. 0,0252 м3/с = 25,2 л/с.
0,0252 м3/с = 25,2 л/с.

 .
. и
и  , получаем:
, получаем: м.
м.

 ;
; 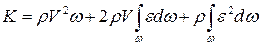 .
. .
. .
. . (3.3.4)
. (3.3.4) , (3.3.5)
, (3.3.5) . (3.3.6)
. (3.3.6)
 = 1,56.
= 1,56.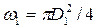 = 0,00785 м2;
= 0,00785 м2; = 0,01767 м2.
= 0,01767 м2. = 3,82 м/с;
= 3,82 м/с; = 1,698 м/с.
= 1,698 м/с.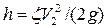 = 0,229 м.
= 0,229 м. = 4190 Па.
= 4190 Па.


