
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные и кусочно-линейные разделяющие функции
Разделяющую функцию часто представляют в виде линейной суммы
где
где Учитывая свойство разделяющих функций, разделяющая поверхность между двумя классами, в общем случае, будет определяться из соотношения
Рассмотрим, например, случай разделения объектов на два класса:
В соответствии с этим решающим правилом операцию автоматического определения номера класса в системе классификации можно записать следующем образом
где
В правильности определения номера класса можно легко убедиться:
Особый случай Для случая
где Рассмотрим подробнее процедуру построения разделяющих функций. Пусть
Отсюда для решающей функции получим
Поскольку
Построим разделяющую поверхность для задачи классификации с двумя классами
Отсюда для разделяющей поверхности (поскольку разделяющая функция линейна, то такой поверхностью, в общем случае, будет гиперплоскость) получим уравнение
Построим разделяющую функцию и разделяющую поверхность системы классификации образов
Предположим, что объект
Если это соотношение выполняется, то предъявляемый объект принадлежит первому классу. Решающая функция в этом случае будет иметь вид
Отсюда легко получить решающее правило
Разделение пространства существенных признаков на две области соответствующие первому и второму классам приведено на рис. 2.13. Границей классов в этом случае является прямая
Для объекта
Необходимо отметить одно важное свойство такого подхода, а именно: разделяющая прямая проходит под прямым углом через середину отрезка (точка Исходя из этого, можно разработать альтернативный метод построения линейных разделяющих функций и поверхностей. Линейной разделяющей функции в многомерном пространстве существенных признаков соответствует гиперплоскость. Уравнение гиперплоскости, проходящей перпендикулярно к отрезку, соединяющему точки соответствующие представителям классов, и через его середину определяет заодно и разделяющую функцию. Следует отметить, что гиперплоскость, удовлетворяющая данным условиям, является единственной. Изложенные принципы разбиения пространства существенных признаков на области классов, используются в тех случаях, когда разделяющие поверхности и соответствующие разделяющие функции являются выпуклыми.
Функция
для любых двух точек
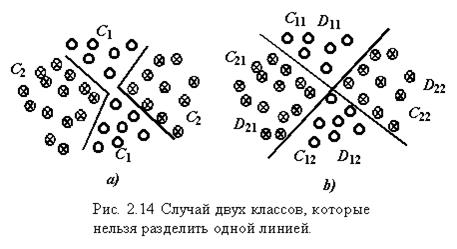
Следует отметить, что не редки ситуации, когда разделяющие функции не являются выпуклыми. На рис. 2.14 приведен случай, когда каждый из двух классов состоит из двух областей: 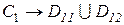 , а , а  . Если считать, что каждый из классов состоит из двух подклассов: . Если считать, что каждый из классов состоит из двух подклассов: 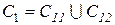 и и  , а каждый из них рассматривать как самостоятельный класс, то для построения системы классификации можно использовать линейные разделяющие функции. В этом случае задача классификации сводится к построению кусочно-линейных разделяющих функций. В рамках такого подхода возможны три различных случая [ Р1 ]: , а каждый из них рассматривать как самостоятельный класс, то для построения системы классификации можно использовать линейные разделяющие функции. В этом случае задача классификации сводится к построению кусочно-линейных разделяющих функций. В рамках такого подхода возможны три различных случая [ Р1 ]:
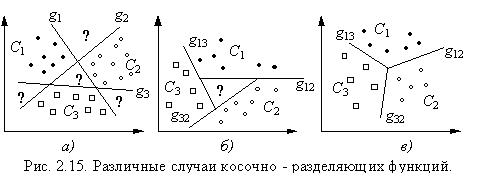
1. Классы разделяются с помощью линейных разделяющих функций. При этом в пространстве образов (пространстве существенных признаков) возникает несколько областей которые не соответствуют ни одному из классов (см. рис. 2.15.а). 2. Каждый класс отделяется от другого, с помощью линейной гиперповерхности, при этом в пространстве образов возникает только одна область, которая не соответствует ни одному из классов (см. рис. 2.15.б). 3.
Пространство образов разделяется только на области соответствующие классам (см. рис. 2.15. в). Для построения кусочно-линейных разделяющих функций можно воспользоваться процедурой предложенной Аркадьевым и Браверманом. Суть этого метода заключается в следующем. Пусть имеется четыре класса
Преобразуем его к виду
Тогда уравнение перпендикуляра к данной прямой проходящего через точку с координатами
Это уравнение заодно определяет разделяющую функцию Теперь необходимо убедиться в правильности классификации с данной разделяющей функцией. Для этого выбираем случайным образом объекты, принадлежащие данным классам, и проверяем, будут ли они правильно классифицированы. В данном случае разделяющая функция обеспечивает правильную классификацию.
Одним из важных этапов в процессе распознавания образов является операция выявления общих характеристик предъявляемых объектов. Группирование объектов по их принадлежности к одному классу может рассматриваться как агрегация, или обобщение, исходных данных. Для этой операции характерны два связанных и в тоже время противоположных действия - объединение подобных и отделение отличающихся объектов. Причем понятие «подобие» или «сходство», должно быть строгим и, по возможности, формализованным. В качестве такой меры сходства объектов можно воспользоваться понятием расстояния, по принципу: чем меньше расстояние Применение этой процедуры к большим массивам данных позволяет не только проводить классификацию, но и выявлять структурные связи между объектами или их частями.
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.13.173 (0.022 с.) |
 , (2.18)
, (2.18)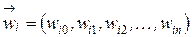 — весовые коэффициенты для класса
— весовые коэффициенты для класса 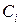 . Каждый весовой коэффициент относится к определенной составляющей вектора существенных признаков. Для удобства записи вводится весовой коэффициент с нулевым индексом
. Каждый весовой коэффициент относится к определенной составляющей вектора существенных признаков. Для удобства записи вводится весовой коэффициент с нулевым индексом  . Это позволяет записать разделяющую функцию в более компактной форме:
. Это позволяет записать разделяющую функцию в более компактной форме: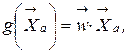 (2.18а)
(2.18а)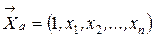 — вектор существенных признаков, в число компонент которого входит дополнительно одна вещественная константа. Ее величину обычно принимают равной единице.
— вектор существенных признаков, в число компонент которого входит дополнительно одна вещественная константа. Ее величину обычно принимают равной единице.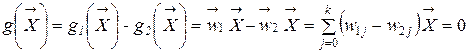 . (2.19)
. (2.19)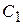 и
и  . Решающее правило
. Решающее правило  для их разделения можно записать в виде:
для их разделения можно записать в виде: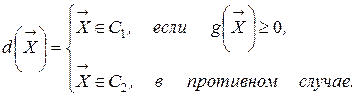 (2.20)
(2.20)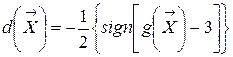 ,
,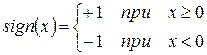 .
.
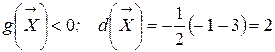 следовательно
следовательно 
 соответствует уравнению поверхности, разделяющей рассматриваемые области. Решение о принадлежности каждой точки этой поверхности принимается произвольно; так, например, можно относить каждую точку этой разделяющей поверхности к классу, имеющему меньший (или больший) индекс, либо использовать какое-нибудь иное правило.
соответствует уравнению поверхности, разделяющей рассматриваемые области. Решение о принадлежности каждой точки этой поверхности принимается произвольно; так, например, можно относить каждую точку этой разделяющей поверхности к классу, имеющему меньший (или больший) индекс, либо использовать какое-нибудь иное правило. сепарабельных классов (
сепарабельных классов ( )
) 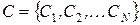 решение о принадлежности объекта к определенному классу будет устанавливаться решающим правилом вида:
решение о принадлежности объекта к определенному классу будет устанавливаться решающим правилом вида: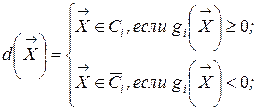 , (2.21)
, (2.21) — дополнение множества
— дополнение множества  , т.е.
, т.е. 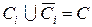 .
.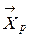 - это вектор измерений существенных признаков объекта, а
- это вектор измерений существенных признаков объекта, а 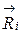
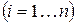 - множество векторов, определяющих эталонные образцы (экземпляры)
- множество векторов, определяющих эталонные образцы (экземпляры)  классов. Классификацию будем осуществлять по принципу наименьшего расстояния между объектом
классов. Классификацию будем осуществлять по принципу наименьшего расстояния между объектом 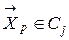 если
если  . При этом расстояния, для определенности, будем вычислять в метрике Евклида. Тогда
. При этом расстояния, для определенности, будем вычислять в метрике Евклида. Тогда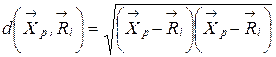 .
. .
. не зависит от
не зависит от  и всегда положительно, то в качестве решающей функции можно использовать линейное соотношение
и всегда положительно, то в качестве решающей функции можно использовать линейное соотношение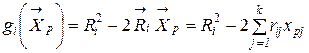 (2.22).
(2.22). и
и 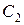 . Очевидно, что на границе между классами разность
. Очевидно, что на границе между классами разность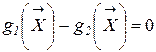 .
.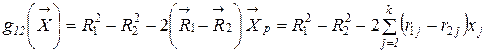 (2.23).
(2.23). с двумя классами при следующих условиях. Пусть представителями этих классов являются объекты:
с двумя классами при следующих условиях. Пусть представителями этих классов являются объекты: 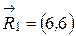 и
и 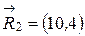 . Построим разделяющие функции для каждого из классов. Вычислим
. Построим разделяющие функции для каждого из классов. Вычислим 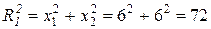 и
и 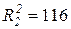 , тогда получим, что
, тогда получим, что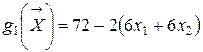 ,
,  .
.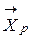 относится к первому классу. Поскольку классификация осуществляется по принципу наименьшего расстояния между
относится к первому классу. Поскольку классификация осуществляется по принципу наименьшего расстояния между  , то в этом случае
, то в этом случае 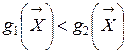 и, следовательно, при построении решающего правила будем использовать соотношение
и, следовательно, при построении решающего правила будем использовать соотношение .
.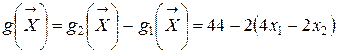 .
.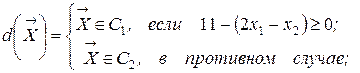 .
.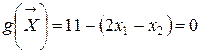 .
. разделяющая функция
разделяющая функция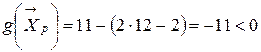 ,
,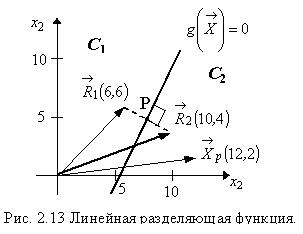 Следовательно, данный объект принадлежит второму классу.
Следовательно, данный объект принадлежит второму классу. ), соединяющего точки
), соединяющего точки 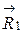 и
и 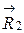 .
.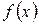 называется выпуклой, если выполняется соотношение
называется выпуклой, если выполняется соотношение
 и
и 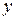 пространства существенных признаков и
пространства существенных признаков и  .
.
 и
и  . Для простоты изложения будем считать, что объекты имеют два существенных признака. В классе
. Для простоты изложения будем считать, что объекты имеют два существенных признака. В классе  выберем случайным образом точку
выберем случайным образом точку 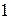 , а в классе
, а в классе 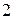 , и соединим их отрезком
, и соединим их отрезком 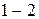 (см. рис. 2.16.). Через середину этого отрезка проведем перпендикуляр. Уравнение этого перпендикуляра – разделяющая функция между классами
(см. рис. 2.16.). Через середину этого отрезка проведем перпендикуляр. Уравнение этого перпендикуляра – разделяющая функция между классами 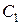 и
и  . Построим эту разделяющую функцию. Уравнение прямой проходящей через две точки с координатами
. Построим эту разделяющую функцию. Уравнение прямой проходящей через две точки с координатами 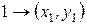 и
и 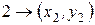 дается соотношением
дается соотношением .
.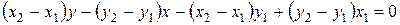 .
.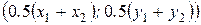 , т.е. через середину отрезка
, т.е. через середину отрезка 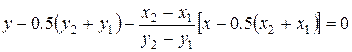 .
.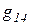 .
. В классе
В классе  выберем случайным образом точку
выберем случайным образом точку 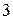 . Соединим ее отрезком с точкой
. Соединим ее отрезком с точкой 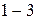 проведем перпендикуляр
проведем перпендикуляр  . Выберем случайным образом контрольную точку
. Выберем случайным образом контрольную точку  , принадлежащую классу
, принадлежащую классу  , принадлежащую классу
, принадлежащую классу  проведем перпендикуляр
проведем перпендикуляр 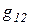 и проверим, обеспечивает ли соответствующая разделяющая функция правильную классификацию. Аналогичным образом необходимо построить разделяющие функции между остальными классами. После того как будут получены все разделяющие функции, обеспечивающие правильную классификацию, исключив лишние можно составить решающее правило. В данном случае оно может выглядеть примерно так:
и проверим, обеспечивает ли соответствующая разделяющая функция правильную классификацию. Аналогичным образом необходимо построить разделяющие функции между остальными классами. После того как будут получены все разделяющие функции, обеспечивающие правильную классификацию, исключив лишние можно составить решающее правило. В данном случае оно может выглядеть примерно так:
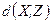 между объектами
между объектами  и
и 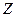 , тем больше сходство между ними.
, тем больше сходство между ними.


