
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения нелинейных уравненийСтр 1 из 7Следующая ⇒
РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Издательство Южного федерального университета
УДК 517.949.8 (076.5) 518.12 (076.5)
Чистяков А.Е., Чистякова Т.А., Никитина А.В., Кузнецова И.Ю.
Современные проблемы прикладной математики и информатики: учебно-методическое пособие. – Ростов-на-Дону ЮФУ, 2016. – 100 с.
Учебно-методическое пособие включает краткое описание достаточно часто употребляемых прямых и итерационных методов решения систем линейных алгебраических уравнений и методов решения нелинейных уравнений. Кроме того, в пособии изложены элементы теории интерполирования, линейного интегрирования, разностных методов решения обыкновенных дифференциальных уравнений. В пособии приведены примеры использования описанных численных методов, а также варианты заданий для самостоятельной работы студентов. Целью работы является обучение студентов работе с задачами, требующими большого объема вычислительной работы, с использованием универсальных решающих программ типа MathCad. Пособие предназначено для студентов всех специальностей, изучающих численные методы и современные проблемы прикладной математики и информатики. Знаком * обозначены вопросы повышенной сложности. Ил.:4 Библиогр.: 58 назв.
Рецензент: доктор физико-математических наук, доцент, зав. отделом математического моделирования ФГБУН Южный математический институт Владикавказского научного центра (ЮМИ ВНЦ) РАН Е.С. Каменецкий.
Ó ЮФУ, 2016
Содержание Введение………………………………………………………………….4 1. Численное интегрирование………………………………...6 1.4. Пример выполнения лабораторной работы №1……………….12 1.5. Варианты заданий к лабораторной работе №1………………...14 2. Методы решения нелинейных уравнений…………...16 2.1. Метод половинного деления…………………………………….16 2.2. Метод хорд (метод линейной интерполяции)………………….17
2.3. Метод секущих…………………………………………………...19 2.4. Метод Ньютона…………………………………………………..21 2.5. Пример выполнения лабораторной работы №2………………..22 2.6. Варианты заданий к лабораторной работе №2………………...26 3. Прямые методы решения систем линейных алгебраических уравнений………………………………….28 3.1. Метод Гаусса для решения систем линейных алгебраических уравнений…………………………………………………………28 3.2. Алгоритм LU-разложения………………………………………31 3.3. Метод прогонки………………………………………………….34 3.4. Пример выполнения лабораторной работы №3………………..38 3.5. Варианты заданий к лабораторной работе №3………………...45 4. Итерационные методы решения систем линейных алгебраических уравнений…………………………………..48 4.1. Итерационные методы Якоби и Зейделя……………………….48 4.2. Каноническая форма итерационных методов………………….50 4.3. Вариационно-итерационные методы решения СЛАУ………...52 4.4. Пример выполнения лабораторной работы №4………………..54 4.5. Варианты заданий к лабораторной работе №4………………...58 5. Методы решения задачи Коши……………………………61 5.1. Метод Эйлера…………………………………………………….61 5.2. Метод Рунге–Кутта………………………………………………62 5.3. Пример выполнения лабораторной работы №5………………..63 5.4. Варианты заданий к лабораторной работе №5………………...67 6. Методы приближения функций…………………………..69 6.1. Интерполяционный полином Лагранжа и Ньютона…………...70 6.2. Интерполяционный кубический сплайн………………………..76 6.3. Понятие о методе наименьших квадратов……………………...77 6.4. Интерполяционный тригонометрический полином…………...80 6.5. Пример выполнения лабораторной работы №6………………..82 6.6. Варианты заданий к лабораторной работе №6………………...93 Библиографический список………………………………………………96 Введение
Невозможно представить себе современную науку без широкого применения методов и средств математики и информатики. К одному из важных методов современной прикладной математики относится математическое моделирование. Сущность этой методологии состоит в замене исходного объекта его «образом» – математической моделью – и дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Этот «третий метод» познания, конструирования, проектирования сочетает в себе многие достоинства как теории, так и эксперимента. Работа не с самим объектом (явлением, процессом), а с его моделью дает возможность безболезненно, относительно быстро и без существенных затрат исследовать его свойства и поведение в любых мыслимых ситуациях (преимущества теории). В то же время вычислительные (компьютерные, симуляционные, имитационные) эксперименты с моделями объектов позволяют, опираясь на мощь современных вычислительных методов и технических инструментов информатики, подробно и глубоко изучать объекты в достаточной полноте, недоступной чисто теоретическим подходам (преимущества эксперимента). Неудивительно, что методология математического моделирования бурно развивается, охватывая все новые сферы – от разработки технических систем и управления ими до анализа сложнейших экономических и социальных процессов.
Элементы математического моделирования использовались с самого начала появления точных наук, и не случайно, что некоторые методы вычислений носят имена таких корифеев науки, как Ньютон и Эйлер, а слово «алгоритм» происходит от имени средневекового арабского ученого Аль-Хорезми. Второе «рождение» этой методологии пришлось на конец 40-х – начало 50-х годов XX века и было обусловлено по крайней мере двумя причинами. Первая из них — появление ЭВМ (компьютеров), хотя и скромных по нынешним меркам, но тем не менее избавивших ученых от огромной по объему рутинной вычислительной работы. Вторая – беспрецедентный социальный заказ – выполнение национальных программ СССР и США по созданию ракетно-ядерного щита, которые не могли быть реализованы традиционными методами. Математическое моделирование справилось с этой задачей: ядерные взрывы и полеты ракет и спутников были предварительно «осуществлены» в недрах ЭВМ с помощью математических моделей и лишь затем претворены на практике. Этот успех во многом определил дальнейшие достижения методологии, без применения которой в развитых странах ни один крупномасштабный технологический, экологический или экономический проект теперь всерьез не рассматривается (сказанное справедливо и по отношению к некоторым социально-политическим проектам). Сейчас математическое моделирование вступает в третий принципиально важный этап своего развития, «встраиваясь» в структуры так называемого информационного общества. Впечатляющий прогресс средств переработки, передачи и хранения информации отвечает мировым тенденциям к усложнению и взаимному проникновению различных сфер человеческой деятельности. Технические, экологические, экономические и иные системы, изучаемые современной наукой, больше не поддаются исследованию (в нужной полноте и точности) обычными теоретическими методами. Прямой натурный эксперимент над ними долог, дорог, часто либо опасен, либо попросту невозможен, так как многие из этих систем существуют в «единственном экземпляре». Цена ошибок и просчетов в обращении с ними недопустимо высока. Поэтому математическое (шире – информационное) моделирование является неизбежной составляющей научно-технического прогресса.
Без владения информационными «ресурсами» нельзя и думать о решении все более укрупняющихся и все более разнообразных проблем, стоящих перед мировым сообществом. Однако информация как таковая зачастую мало что дает для анализа и прогноза, для принятия решений и контроля за их исполнением. Нужны надежные способы переработки информационного «сырья» в готовый «продукт», т. е. в точное знание. История методологии прикладной математики и информатики убеждает: они могут и должны быть интеллектуальным ядром информационных технологий, всего процесса информатизации общества. К основным проблемам прикладной математики информатики можно отнести: проблему обеспечения надёжности вычислений при ограничении точности исходных данных; изучение корректных, некорректных и промежуточных задач, изменения корректности при преобразованиях; устойчивость полученных решений; общую проблему надёжности вычислений и корректности математических моделей; методы избегания ошибок при применении стандартных прикладных программ MATLAB, MATHCAD и др.; тендем «жёстких» и «мягких» математических моделей; интервальные числа и их свойства; алгебраические системы интервальных чисел; задачи анализа и линейной алгебры в интервальной математике; интервальные методы решения дифференциальных уравнений; проблемы реализации интервальных методов на компьютере. К одной из важных проблем прикладной математики и информатики можно отнести улучшение точности и сокращение времени решения СЛАУ большой размерности с самосопряженными и несамосопряженными операторами, а также плохо обусловленными матрицами. При математическом моделировании различных гидрофизических и биологических процессов возникает необходимость разработки новых методов решения систем нелинейных уравнений. При статистической обработке результатов натурных измерений проявляется потребность в разработке различных методов приближения функций, используемых для прогнозирования состояния моделируемых процессов. Рассматриваемая проблематика дисциплины может включать обсуждения таких разделов, как: «Современные вычислительные методы», «Вычислительные платформы, средства и методы программирования», «Математическое моделирование в науке и технике» и др. Весь материал пособия разбит на 6 лабораторных работ. На каждом занятии студент получает индивидуальное задание, которое выполняет самостоятельно под руководством преподавателя. Варианты заданий приведены в конце каждой лабораторной работы. Там же приведен порядок выполнения работ, показаны соответствующие способы решения поставленных задач с помощью пакета MathCad, приведено содержание отчета. После выполнения каждой лабораторной работы студент должен сделать выводы о проделанной работе.
Для решения математических задач в инженерной практике используются графические, аналитические и численные методы. Графические методы позволяют оценить порядок искомой величины. Основная идея этих методов состоит в том, что решение поставленной математической задачи находится путем геометрических построений. При использовании аналитических методов решение задачи удается выразить с помощью формул. В частности, если математическая задача состоит в решении простейших алгебраических или трансцендентных уравнений, дифференциальных уравнений и т.п., то использование известных из курса математики приемов сразу приводит к цели. К сожалению, на практике это слишком редкие случаи. Основным инструментом для решения сложных математических задач в настоящее время являются численные методы, позволяющие свести решение задачи к выполнению конечного числа арифметических действий над числами; при этом результаты получаются в виде числовых значений. Многие численные методы разработаны давно, однако при вычислениях вручную они могли использоваться лишь для решения не слишком трудоемких задач. Учебно-методическое пособие по курсу «Современные проблемы прикладной математики и информатики» содержит краткое описание наиболее широко используемых на практике методов решения систем линейных алгебраических уравнений, элементы теории интерполирования и численного интегрирования.
Численное интегрирование В этом параграфе будут описаны основные методы численного интегрирования, такие как метод прямоугольников, трапеций и метод Симпсона. Рассмотрим различные способы приближенного вычисления определенного интеграла вида
основанные на замене этого интеграла конечной суммой
где
называется квадратурной формулой, а сумма вида (1.2) – квадратурной суммой. Точки
называется погрешностью квадратурной формулы. Погрешность зависит как от расположения узлов, так и от выбора коэффициентов. При оценке погрешности в приводимых ниже примерах функция Введем на
и представим интеграл (1.1) в виде суммы интегралов по частичным отрезкам:
Для построения формулы численного интегрирования на всем отрезке
на частичном отрезке
Метод прямоугольников Пользуясь малостью Тогда получим формулу
которая называется формулой прямоугольников на частичном отрезке Погрешность формулы (1.4) определяется величиной
которую легко оценить с помощью формулы Тейлора. Действительно, запишем
и воспользуемся разложением
где
Обозначая
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка
т.е. формула имеет погрешность Заметим, что оценка (1.6) является не улучшаемой, т.е. существует функция
Суммируя равенства (1.4) по
Погрешность этой формулы
равна сумме погрешностей по всем частичным отрезкам,
Отсюда, обозначая
т.е. погрешность формулы прямоугольников на всем отрезке есть величина В этом случае говорят, что квадратурная формула имеет второй порядок точности. Замечание. Можно также использовать формулы прямоугольников при ином расположении узлов, например, такие формулы (формулы левых и правых прямоугольников соответственно):
Однако из-за нарушения симметрии погрешность таких формул является величиной
Метод трапеций На частичном отрезке
и получается путем замены подынтегральной функции
Для оценки погрешности достаточно вспомнить, что
Отсюда получим
и, следовательно,
Оценка (1.10) не улучшаема, так как в ней достигается равенство, например, для Составная формула трапеций имеет вид
где Погрешность этой формулы оценивается следующим образом:
Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности
Метод Симпсона При аппроксимации интеграла (1.3) заменим функцию
где
Проводя интегрирование, получим
Таким образом, приходим к приближенному равенству
которое называется формулой Симпсона или формулой парабол. На всем отрезке
Чтобы не использовать дробных индексов, можно обозначить
и записать формулу Симпсона в виде
Прежде чем переходить к оценке погрешности формулы (1.13), заметим, что она является точной для любого многочлена третьей степени, т.е. имеет место точное равенство
Если Для оценки погрешности формулы Симпсона построим многочлен третьей степени
Известно, что такой многочлен существует и единственен. Он построен в явном виде. Однако нам даже не потребуется явный вид многочлена
Представим теперь
где
Имеем
поэтому для погрешности
где Вычисляя интеграл, приходим окончательно к оценке
Погрешность составной формулы Симпсона (1.14) оценивается так:
Отсюда видно, что формула Симпсона существенно точнее, чем формулы прямоугольников и трапеций. На частичном отрезке она имеет точность
Пример выполнения лабораторной работы №1 Применим методы численного интегрирования для приближенного вычисления интеграла Алгоритм решения поставленной задачи в с использованием универсальных решающих программ типа MathCad. 1. Задаем число разбиений
2. Устанавливаем пределы интегрирования
3. Вычисляем шаг сетки
4. Вводим подынтегральную функцию
5. Рассчитываем точное значение интеграла
6. Рассчитываем значение интеграла методом левых прямоугольников
7. Выводим полученное значение
8. Выводим значение погрешности в случае использования левых прямоугольников
9. Рассчитываем значение интеграла и погрешности методом правых прямоугольников
10. Рассчитываем значение интеграла и погрешности методом центральных прямоугольников
11. Рассчитываем значение интеграла и погрешности методом трапеций
12. Рассчитываем значение интеграла и погрешности методом Симпсона
Варианты заданий к лабораторной работе №1
Примените методы численного интегрирования для вычисления следующих интегралов:
1. 2. 3. 4. 5.
Содержание отчета Отчет должен содержать: 1) титульный лист; 2) постановку задачи (согласно варианту); 3) краткое описание методов численного интегрирования; 4) программную реализацию данных методов; 5) выводы о проделанной работе.
Контрольные вопросы и задания 1. Какие методы численного интегрирования вы знаете? 2. Какой из методов численного интегрирования, в вашем случае, оказался наиболее точным, а какой – наименее точным? 3. Чему равна погрешность численного интегрирования для вышеизложенных методов? 4. Запишите формулы для приближенного вычисления определенных интегралов. 5. Вычислите определенный интеграл с помощью методов численного интегрирования. 6. Для заданного примера найдите теоретическую и практическую погрешность численного вычисления определенных интегралов. 7. Сравните погрешность методов трапеций и центральных прямоугольников. 8. Как еще называется формула Симпсона и почему? 9. Запишите формулу для расчета погрешности методов численного интегрирования. 10.* Запишите формулу Симпсона через линейную комбинацию формул трапеций и центральных прямоугольников. Теорема Больцано–Коши Если непрерывная на отрезке
то на интервале
Метод половинного деления
Предположим, что существует корень на отрезке Положим Далее повторим процесс для отрезка
Рис. 2.1. Последовательное деление отрезка пополам и приближение к корню
Поступая тем же образом и далее, получаем, что после
то расстояние от корня
Метод секущих
Идея метода секущих состоит в том, что выбирают любую постоянную
и на каждой итерации нужно один раз вычислить значение функции Выясним смысл этой формулы, а также смысл условия о совпадении знаков
Найдём точку пересечения этой прямой с осью
откуда Замечание. Значение производной вычислять не обязательно, достаточно лишь знать, убывает функция В качестве следующего приближения к корню берётся точка пересечения построенной прямой с осью
Рис. 2.3. Последовательные итерации метода секущих
На чертеже изображены итерации. Мы видим, что последовательные точки Метод Ньютона
Рассмотрим эффективный метод решения нелинейных уравнений, носящий имя Ньютона. Вначале приведем некоторые наводящие рассуждения. Пусть функция
Пренебрежем остаточным членом порядка Тогда имеем приближенное равенство
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.196.211 (0.205 с.) |

 Ростов-на-Дону
Ростов-на-Дону

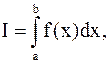

 – числовые коэффициенты и
– числовые коэффициенты и  – точки отрезка
– точки отрезка  ,
, 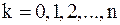 . Приближенное равенство
. Приближенное равенство

 предполагается достаточно гладкой.
предполагается достаточно гладкой. , т.е. множество точек
, т.е. множество точек ,
,

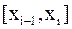 и воспользоваться свойством аддитивности определенного интеграла.
и воспользоваться свойством аддитивности определенного интеграла. , где
, где  .
.

 в виде
в виде

 . Тогда из (1.5) получим
. Тогда из (1.5) получим
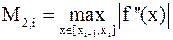 , оценим
, оценим 
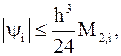
 при
при  .
. имеем
имеем  ,
,  и
и
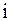 от
от 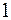 до
до 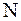 , получим составную формулу прямоугольников (центральных прямоугольников):
, получим составную формулу прямоугольников (центральных прямоугольников):


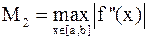 , получим
, получим
 .
.
 .
.
 интерполяционным многочленом первой степени, построенным по узлам
интерполяционным многочленом первой степени, построенным по узлам  , т.е. функцией
, т.е. функцией



 .
.
 .
.
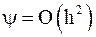 , но ее погрешность оценивается величиной в два раза меньшей (см. (1.8)).
, но ее погрешность оценивается величиной в два раза меньшей (см. (1.8)).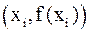 ,
,  , т.е. представим приближенно
, т.е. представим приближенно  ,
, – интерполяционный многочлен Лагранжа второй степени,
– интерполяционный многочлен Лагранжа второй степени,
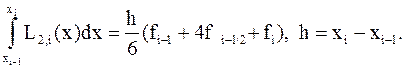

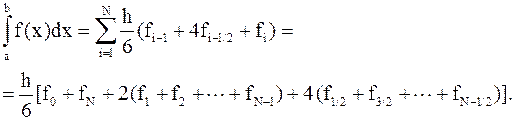
 ,
,  ,
, 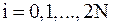 ,
, 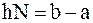

 .
.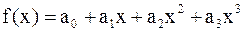 , это утверждение нетрудно проверить непосредственно, что и предоставляется сделать читателю.
, это утверждение нетрудно проверить непосредственно, что и предоставляется сделать читателю. такой, что
такой, что ,
,  ,
, 


 ,
,
 – погрешность интерполирования многочленом
– погрешность интерполирования многочленом 


 .
.

 , а на всем отрезке –
, а на всем отрезке –  .
. .
. .
. .
.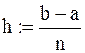 .
. .
.
 .
. .
. .
. .
.
 .
. .
.

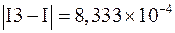 .
.

 .
.

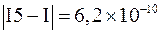 .
. ; 6.
; 6.  ;
; ; 7.
; 7.  ;
; ; 8.
; 8. 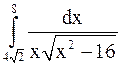 ;
; ; 9.
; 9.  ;
; ; 10.
; 10.  ,
, она хотя бы один раз обращается в ноль.
она хотя бы один раз обращается в ноль. и
и  различны (функция
различны (функция  ).
).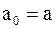 и
и  и вычислим значения функции в левом конце отрезка, т.е. найдем
и вычислим значения функции в левом конце отрезка, т.е. найдем  , и в его середине
, и в его середине  , найдем
, найдем  . Сравним знаки чисел
. Сравним знаки чисел  ; если же одинаковы, то тогда различны знаки
; если же одинаковы, то тогда различны знаки  , и корень лежит в интервале
, и корень лежит в интервале  . (Возможен ещё случай
. (Возможен ещё случай  ; тогда корень
; тогда корень  уже найден). В обоих случаях смены знака корень оказывается отделённым на отрезке
уже найден). В обоих случаях смены знака корень оказывается отделённым на отрезке  либо
либо  , длина которого ровно в два раза меньше длины исходного отрезка
, длина которого ровно в два раза меньше длины исходного отрезка 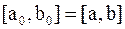 . Обозначим этот отрезок половинной длины через
. Обозначим этот отрезок половинной длины через  (положим
(положим  в случае, когда
в случае, когда  в случае, когда
в случае, когда  , найдём значение функции
, найдём значение функции  и сравним знак этого числа со знаком
и сравним знак этого числа со знаком  ; если знаки разные, то корень отделён на
; если знаки разные, то корень отделён на  , если одинаковые, то на
, если одинаковые, то на  (или же оказывается, что
(или же оказывается, что  ; тогда корень найден). Длина отрезка, на котором отделён корень, уменьшилась ещё в два раза.
; тогда корень найден). Длина отрезка, на котором отделён корень, уменьшилась ещё в два раза.
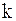 делений длина отрезка, на котором лежит корень, сокращается в
делений длина отрезка, на котором лежит корень, сокращается в  раз и становится равной
раз и становится равной 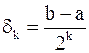 (если корень не был точно определён на каком-то предыдущем этапе, т. е. не совпал с
(если корень не был точно определён на каком-то предыдущем этапе, т. е. не совпал с  при некотором
при некотором  – заданная точность, с которой требуется отыскать корень. Процесс деления отрезков следует остановить, как только станет верным неравенство
– заданная точность, с которой требуется отыскать корень. Процесс деления отрезков следует остановить, как только станет верным неравенство  . Очевидно, что если при этом положить в качестве корня
. Очевидно, что если при этом положить в качестве корня ,
, , до середины этого интервала
, до середины этого интервала 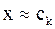 будет выполнено с нужной точностью.
будет выполнено с нужной точностью. , знак которой совпадает со знаком производной
, знак которой совпадает со знаком производной  в окрестности
в окрестности  (и в частности на отрезке, соединяющем
(и в частности на отрезке, соединяющем  и
и 
 и
и  на графике
на графике 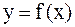 с угловым коэффициентом
с угловым коэффициентом 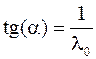 . Тогда уравнением этой прямой будет
. Тогда уравнением этой прямой будет .
. из уравнения
из уравнения
 . Следовательно, эта прямая пересекает ось
. Следовательно, эта прямая пересекает ось  того же знака, что производная
того же знака, что производная  .
. , имеют один и тот же угловой коэффициент
, имеют один и тот же угловой коэффициент 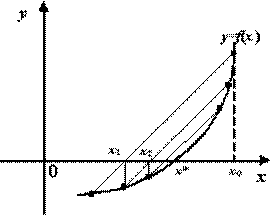
 , корень которой ищется, имеет производные до 2-го порядка в окрестности корня – точки
, корень которой ищется, имеет производные до 2-го порядка в окрестности корня – точки  . Пусть уже найдено
. Пусть уже найдено  -е приближение к корню (на
-е приближение к корню (на 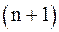 -е приближение. По формуле Тейлора имеем
-е приближение. По формуле Тейлора имеем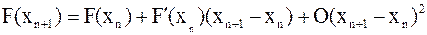 .
. в правой части формулы и будем считать, что
в правой части формулы и будем считать, что  , т.е. приближение номера
, т.е. приближение номера 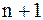 найдено столь точно, что
найдено столь точно, что  .
.


