Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 3. Интеграл и его приложенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Интегрирование - это действие обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. В рекомендуемых учебных пособиях необходимо ознакомиться со следующими краткими сведениями справочного характера по интегральному исчислению. Неопределенный интеграл: -понятие первообразной данной функции; - определение неопределенного интеграла; - основные свойства неопределенного интеграла; - таблица основных неопределённых интегралов; - применение основных свойств и таблицы неопределенных интегралов, непосредственное интегрирование; - метод подстановки. Определенный интеграл: - определение и свойства определенного интеграла; - определённый интеграл как площадь криволинейной трапеции, его принципиальное отличие от неопределенного интеграла; - вычисление определённого интеграла. Формула Ньютона-Лейбница. - замена переменной в определенном интеграле; - вычисление площадей плоских фигур и объёмов тел вращения; - использование определенного интеграла при решении задач прикладного характера. В результате изучения темы студент должен: Уметь: - находить неопределённые интегралы, сводящиеся к табличным, с помощью основных свойств и простых преобразований; - восстанавливать закон движения по заданной скорости, скорость по ускорению, количество электричества по силе тока и др.; - вычислять определённый интеграл с помощью основных его свойств и формулы Ньютона-Лейбница; - находить площади криволинейных трапеций; - решать простейшие прикладные задачи, сводящиеся к составлению и вычислению интеграла. использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: - решения прикладных задач на вычисление в простейших случаях площадей и объемов с использованием определенного интеграла;
Приведём основные свойствами неопределенного интеграла: 1) постоянный множитель (к¹0) можно выносить за знак интеграла:
2) интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций
3) 4) 5)
Основные формулы интегрирования Приведем таблицу основных неопределенных интегралов:
Справедливость этих формул можно проверить путем дифференцирования, т.е. легко убедиться в том, что производные от правых частей формул будут равны соответствующим подынтегральным функциям. Интегралы таблицы называются табличными.
Основные методы интегрирования. Непосредственное интегрирование – это такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам. Интегрирование методом подстановки (замены переменной). Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае используют метод подстановки. Для интегрирования методом постановки будем использовать следующую схему: 1. Часть подынтегральной функции заменим новой переменной; 2. Найдем дифференциал от обеих частей замены; 3. Выразим подынтегральное выражение через новую переменную (после чего должен получиться табличный интеграл); 4. Найдем полученный табличный интеграл; 5. Сделаем обратную замену, вернемся к старой переменной.
Определенный интеграл Определение. Если
Непосредственное вычисление определенного интеграла В отличие от неопределенного интеграла, представляющего собой совокупность всех первообразных от данной функции, определенный интеграл есть число. Для его вычисления применяют формулу Ньютона- Лейбница
где Т. е. значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции при нижнем и верхнем пределах интегрирования. Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов. Если функция Основные свойства определенного интеграла
Вопросы для самоконтроля 1. Какая связь существует между операциями дифференцирования и интегрирования? 2. Какая функция называется первообразной для заданной функции? 3. Дайте определение неопределенного интеграла. 4. Назовите основные свойства неопределенного интеграла. 5. Перечислите основные табличные интегралы. 6. Запишите формулу Ньютона- Лейбница. 7. Объясните, почему она называется формулой, выражающей связь определённого интеграла с неопределённым? Где в ней неопределённый интеграл? 8. В чём принципиальное различие неопределённого и определённого интегралов? 9. Какую фигуру называют криволинейной трапецией? 10. Запишите формулу для вычисления площади криволинейной трапеции. 11. В чем заключается геометрический смысл определённого интеграла? 12. Запишите основные свойства определенного интеграла. 13. Какие методы вычисления определенного интеграла Вам известны? 14. Назовите несколько примеров применения определенного интеграла в геометрии и физике.
|
||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1712; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 .
. .
.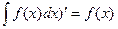 или
или 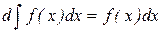 .
.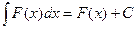 или
или  .
. .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;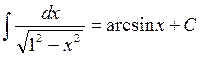 ;
;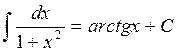 ;
; -первообразная функция для
-первообразная функция для  , то приращение
, то приращение 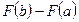 первообразных функций при изменении аргумента
первообразных функций при изменении аргумента 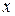 от
от  до
до 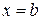 называется определенным интегралом и обозначается
называется определенным интегралом и обозначается т.е.
т.е. 
 - нижний, а
- нижний, а  - верхний пределы определенного интеграла.
- верхний пределы определенного интеграла. , прямыми
, прямыми  и отрезком оси Ox). В этом заключается геометрический смысл определенного интеграла. Таким образом, площадь криволинейной трапеции можно вычислить по формуле:
и отрезком оси Ox). В этом заключается геометрический смысл определенного интеграла. Таким образом, площадь криволинейной трапеции можно вычислить по формуле:  .
.