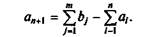Формулировка и методы решения транспортной задачи

Оптимальное закрепление поставщиков однородного груза за потребителями, т.е. нахождение оптимальных грузопотоков, яв­ляется классическим примером транспортной задачи. Эта задача возникает, когда несколько поставщиков имеют однородный груз (несколько складов инертных грузов, контейнерных площадок и т.д.), который в определенных объемах должен быть доставлен потребителям.

В этом случае потребителя не интересует, с какого конкретно склада ему будет доставлен, например, щебень. Но с точки зре­ния снижения транспортных издержек может наблюдаться сущест­венная разница. Уменьшение расстояния перевозки грузов от по­ставщиков к потребителям в этом случае будет являться основ­ным резервом снижения транспортных издержек.

В отдельных случаях транспортная задача может решаться не только для определения минимума пробега, который будет вы­полнен для доставки груза, но и для определения наиболее ко­роткого времени, требуемого для выполнения перевозок, или их минимальной стоимости. В этом случае вместо матрицы расстоя­ний между поставщиками и потребителями необходимо исполь­зовать матрицы времени движения или стоимости перевозок. Так как в подавляющем большинстве случаев перевозчик заинтересо­ван в минимизации пробега, то в дальнейшем будет рассматри­ваться транспортная задача только на определение минимума рас­стояния (грузооборота).

Суть транспортной задачи линейного программирования состоит в следующем. В пунктах отправления А₁, А₂,..., A_n имеется одно­родный груз в количестве а₁, а₂,..., а_n. Этот груз необходимо до­ставить в пункты потребления В₁, В₂,..., В_т в количестве b ₁ b₂,..., b _т. Известны кратчайшие расстояния с_ij между всеми пунктами отправления и получения груза. Необходимо построить план пере­возок таким образом, чтобы была удовлетворена потребность в грузе всех пунктов потребления, был бы вывезен весь груз из пун­ктов производства и при этом был бы обеспечен минимум транс­портной работы в тонна-километрах.

Экономико-математическая модель транспортной задачи вы­глядит следующим образом.

Система ограничений по количеству груза, доставляемого в Пункты потребления:

 

 

Система ограничений по количеству груза, вывозимого из каждого пункта производства:

где x _ij — объем перевозок между i-и и j-й точками транспорт ной сети; i — количество поставщиков; j — количество потре бителей; а, — ограничения по предложению; b _j — ограничение по спросу.

Причем предполагается, что

так как это необходимо для совместимости системы уравнений

Общий объем транспортной работы (стоимости перевозок) должен быть минимальным. Поэтому целевая функция выглядит следующим образом:

Математическая постановка задачи показывает, что задача крепления поставщиков за потребителями относится к классу задач линейного программирования. Но есть некоторые особенности, которые позволяют говорить об этой задаче особо:

• в уравнениях коэффициенты при неизвестных принимают только два значения: 0 или 1;

• каждая переменная только дважды встречается с коэффициентом равным 1, а в остальных случаях ее коэффициенты; равны 0.

Благодаря этим особенностям, задача закрепления поставщиков за потребителями выделена в специальный класс и называет ся транспортной задачей линейного программирования. Условия транспортной задачи обычно представляются в виде матрицы образец которой приведен в табл. 8.1.

В практике планирования ГАП встречаются особые виды транс портных задач.

 

 

Модели с несбалансированным спросом и предложением получили название открытых. В таких задачах спрос и предложение не сба­лансированы.

Если спрос превышает предложение, то вводится фиктивный ГОП, для которого объем вывоза груза составит

Если у отправителя груза больше, чем требуется потребителю, то вводится фиктивный ГПП, для которого объем завоза груза составит

Расстояния для фиктивного ГОП или ГПП принимаются рав­ными нулю.

Модель с запрещенными корреспонденциями используется, если какие-либо ГПП не могут получать груз из некоторых ГОП. В этом случае между ними вводится очень большое расстояние, суще­ственно превышающее реальное.

Модель с обязательными корреспонденциями используется, если какие-либо ГПП должны получать груз из конкретных ГОП. В этом случае корректируются ограничения.

Учитывая специфику транспортной задачи, для ее решения наиболее эффективными оказались специальные методы, позво­ляющие из бесчисленного множества решений найти оптималь­ное. Одним из таких методов является распределительный метод.

В основе математических методов, применяемых при решении транспортных задач (в том числе распределительного метода), лежит принцип последовательного улучшения плана. Сначала оп­ределяется первоначальное допустимое решение задачи, а затем это решение проверяется на оптимальность и при необходимости улучшается. Процесс продолжается до тех пор, пока не будет по­лучено оптимальное решение.

От того, насколько эффективно составлено допустимое рас­пределение перевозок на начальном плане, зависит количество промежуточных итераций, необходимых для получения конечно­го оптимального решения. Первоначальное допустимое распреде­ление может быть получено несколькими способами. Рассмотрим некоторые из них.

Построение допустимого первоначального плана методом се­веро-западного угла начинается с заполнения левой верхней клет­ки матрицы и заканчивается в правой нижней клетке матрицы. В каждую клетку заносят максимально возможную поставку, учи­тывая при этом возможности поставщика и спрос потребителя.

Груз, имеющийся у первого поставщика, распределяется так, чтобы сначала по возможности полностью удовлетворить потреб­ности первого потребителя, потом второго и т.д. Затем переходят к распределению груза, имеющегося у второго поставщика, и так до полного распределения груза у всех поставщиков. Если спрос какого-либо потребителя превышает наличие груза у поставщи­ка, то недостающий спрос удовлетворяют за счет следующего поставщика.

Способ построения первоначального допустимого плана мето­дом северо-западного угла очень прост, но, как правило, полу­ченный план далек от оптимального. Это объясняется тем, что составление плана производится механически, без учета расстоя­ний между пунктами или стоимости перевозок.

При построении первого допустимого решения методом аппроксимации Фогеля полученное распределение близко к оптималь­ному и по сути является приближенным решением задачи.

При этом способе исходная матрица дополняется столбцом и строкой разностей. Затем в каждой строке и в каждом столбце матрицы находят два наименьших расстояния между пунктами и вычисляют разность между ними. Полученный результат заносят в соответствующую ячейку строки или столбца разностей, причем разности по строке — в столбец разностей, а разности по столб­цам — в строку разностей. Если две ячейки матрицы в одной стро­ке или в одном столбце имеют одинаковое наименьшее значение, разность для этой строки или столбца принимается равной нулю и тоже заносится в соответствующую ячейку.

Затем выбирают наибольшее значение разности независимо от того, в строке или столбце разностей она находится. В данной строке или столбце находят клетку с минимальным расстоянием между | пунктами. В эту клетку заносят максимально возможную загрузку, учитывая при этом соотношение ресурса поставщика и спроса потребителя.

При наличии нескольких разностей, имеющих одинаковое наи­большее значение, находят седловую точку. Для этого необходимо найти среди всех клеток в строках или столбцах, соответствующих наибольшим разностям, клетку с минимальным расстоянием меж­ду пунктами. Такая клетка будет называться седловой точкой.

Если при закреплении очередной загрузки оказалось, что спрос потребителя полностью удовлетворен или ресурс поставщика пол­ностью исчерпан, то в соответствующей строке или столбце раз­ностей проставляется буква К (конец), в остальных свободных ячейках строки или столбца проставляется знак «х» и данная строка или столбец матрицы из дальнейшего рассмотрения исключается.

После этого пересчитываются столбец или строка разностей, и процесс повторяется до тех пор, пока не будет получено допу­стимое распределение загрузки.

Для проверки оптимальности полученного распределения перево­зок находят специальные вспомогательные показатели для строк и и столбцов v, называемые потенциалами. Для каждой загружен­ной клетки сумма соответствующих этой клетке потенциалов дол­жна быть равна расстоянию между пунктами, указанному в этой клетке. В соответствии с этим потенциалы можно определить по следующему правилу.

Одному из столбцов или строк присваивается потенциал, рав­ный нулю. Это может быть любой столбец или строка, но целесо­образно приравнять к нулю потенциал того столбца (или строки), в котором содержится загруженная клетка с наибольшим рассто­янием между пунктами.

Затем определяем потенциалы остальных столбцов и строк, исходя из того, что и + v = с, при этом определяем потенциалы только строк и столбцов, содержащих загруженные клетки. Для того чтобы определить потенциалы всех столбцов и строк в мат­рице, необходимо, чтобы матрица содержала не менее (п + т- 1) загруженных клеток.

Если количество загруженных клеток меньше, чем (п + т- 1), необходимо искусственно загрузить недостающее количество кле­ток матрицы, для чего в эти клетки записывается нулевая загруз­ка. Подстановка нулевой загрузки никак не влияет на соотноше­ние спроса и потребления. Ноль следует приписывать той клетке, которая лежит на пересечении строки или столбца, не имеющих потенциала, со строкой или столбцом, потенциал которых уже определен. В этом случае будет возможно определить еще неопре­деленный потенциал строки или столбца.

Если потенциалы во всех незагруженных клетках меньше, чем расстояние между пунктами в этой же клетке, то найденное рас­пределение плана перевозок является оптимальным.

Следующим этапом в построении оптимального плана распре­деления загрузок является этап улучшения полученного распределе­ния. Чем ближе первый допустимый план загрузки к оптимальному плану, тем меньшее количество итераций на этом этапе необхо­димо для преобразования первоначального плана в оптимальный.

Для оптимизации первоначального допустимого плана перево­зок необходимо построить контур для наиболее потенциальной клетки. Будем считать наиболее потенциальной такую клетку, для которой разность между вычисленным потенциалом клетки и со­ответствующим этой клетке расстоянием является максималь­ной.

Контуром называется замкнутая ломаная линия, образованна прямыми отрезками, углы соединений между которыми равны 90°. Строится контур так, чтобы все углы кроме одного располага­лись в загруженных клетках, а один угол находился в незагружен­ной, наиболее потенциальной клетке. От выбранной незагружен­ной клетки проводят прямую линию по строке или столбцу до загруженной клетки, которой в свою очередь должна соответство вать еще одна загруженная клетка, расположенная под прямь углом, и так до тех пор, пока контур не замкнется в исходной клетке. При соблюдении этих правил для каждой незагруженной ячейки матрицы можно построить только один контур.

Виды контуров могут быть весьма разнообразными (рис. 8.4) Но следует иметь в виду, что число вершин контура всегда будет четным. При этом те клетки, где горизонтальные и вертикальные линии пересекаются, нельзя считать вершинами контура. Верши­ной контура является лишь та ячейка, где эти линии образуют прямой угол.

После того как построен контур для наиболее потенциальной клетки, всем вершинам контура присваиваются попеременно зна ки «+» и «-». Начинать надо с клетки, выбранной для начала построения контура (это незагруженная клетка), ей присваива ется знак «-».

Затем из всех клеток, обозначенных знаком «+», выбирают на именыпую загрузку. Величину этой загрузки вычитают из величи­ны загрузки во всех клетках, помеченных знаком «+», и прибавля ют к величине загрузки в клетках со знаком «-».

 

 

В результате этих действий наиболее потенциальная клетка ста­новится загруженной и одна (или несколько) загруженных кле­ток становятся свободными.

Если при перераспределении загрузки из клеток со знаком «+» в клетки со знаком «-» в матрице одновременно освобождаются не одна, а две клетки (это происходит, если две вершины контура имеют одинаковую минимальную загрузку), то необходимо од­ной из освободившихся клеток присвоить нулевую загрузку.

В том случае, если минимальной загрузкой в клетках со знаком «+» является нулевая загрузка, с ней следует поступать как с ре­альной загрузкой. Поэтому нулевую загрузку необходимо перене­сти в клетку, выбранную для начала построения контура, а в ос­тальных клетках загрузка не изменится.

Полученное распределение загрузок записывают в новую мат­рицу, загрузки тех клеток, которые не являлись вершинами кон­тура, переносятся без изменений. Для вновь полученного распре­деления загрузок снова проводят проверку на оптимальность, и, если полученный вариант не является оптимальным, снова про­изводят улучшение плана загрузок. Процесс продолжается до тех пор, пока не будет получено оптимальное распределение загрузок.

В случае, если потенциал одной или нескольких незагружен­ных клеток в матрице распределения загрузок равен расстоянию между пунктами, соответствующему этой ячейке, можно полу­чить несколько оптимальных распределений. Это делается путем построения контура для одной из таких клеток и перемещением по этому контуру наименьшей загрузки точно так же, как было описано ранее.