Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 5. Нелінійні статичні моделі
1.5.1. Загальні поняття про нелінійну модель Якщо зв’язок між змінними величинами, які входять у модель, або функція мети є нелінійними, то модель належить до класу нелінійних. Можливі такі випадки:
а)
б)
в)
У випадку а) функція мети є лінійною, а обмеження нелінійними. У випадку б) функція мети є нелінійною, а обмеження - лінійними. У випадку в) і функція мети, і обмеження є нелінійними. Нелінійна модель на відміну від лінійної має такі особливості: · область допустимих розв’язків може бути неопуклою, складатися з відокремлених підмножин; · функція мети може бути неопуклою; · точки екстремуму функції мети можуть знаходитися як на границі області допустимих розв’язків, так і в середині області. Зрозуміло, що для розв’язування нелінійних задач слід використовувати спеціальні методи, оскільки алгоритм симплексного методу, який вживається для знаходження оптимального розв’язку лінійних задач, базується на опуклості функції мети, що забезпечує співпадіння локального оптимуму з глобальним, на опуклості області допустимих розв’язків та на існуванні екстремуму функції мети на границі області допустимих розв’язків.
1.5.2. Метод множників Лагранжа Розглянемо частинний випадок нелінійної задачі:
де (1.107) - нелінійна функція мети від n змінних величин; (1.108) - нелінійні обмеження; bi - сталі величини. На змінні величини xj не покладається умова невід’ємності, що дає змогу розглядати задачу (1.107) - (1.108) як класичну задачу умовної оптимізації. Допустимо, що функції f(x), gi(x) є неперервними разом із своїми частинними похідними. Перейдемо від задачі умовної до задачі безумовної оптимізації шляхом побудови функції Лагранжа:
Необхідною умовою існування екстремуму функції Лагранжа буде:
Кожен розв’язок системи рівнянь (1.110) визначає можливу точку екстремуму Х0=(х10,...,хn0). Для лінійної задачі
функція Лагранжа прийме такий вигляд:
Необхідною умовою існування екстремуму функції Лагранжа буде:
Якщо задачу (1.107) - (1.108) доповнити умовою xj³0, що є типовим обмеженням в економічних задачах, то необхідна умова існування екстремуму функції Лагранжа для задачі:
описується теоремою Куна-Такера. За теоремою Куна-Такера точка Х0=(х10,...,хn0) буде розв’язком задачі (1.116) - (1.118) лише тоді, коли знайдеться такий вектор l0=(l10,...,lm0) при якому для функції Лагранжа
в точці (Х0; l0) будуть виконуватися такі умови:
Для загальної задачі лінійного програмування
функція Лагранжа набере вигляду
а необхідна умова існування екстремуму функції опишеться системою обмежень:
1.5.3. Множники Лагранжа і двоїсті оцінки задачі лінійного програмування
Розглянемо задачу лінійного програмування
яку перетворимо до вигляду
Позначимо множники Лагранжа для задачі (1.134) - (1.137) через хj і побудуємо функцію Лагранжа:
Умови Куна-Такера для функції Лагранжа (1.138) можна записати в такому вигляді:
Очевидно, що умови (1.139), (1.141), (1.144) для задачі (1.131) - (1.133) співпадають з обмеженнями (1.126), (1.128), (1.129) для загальної задачі лінійного програмування, а обмеження (1.140), (1.142), (1.143) - з обмеженнями (1.125), (1.127), (1.130). Подібна пара задач називається двоїстою. Множники Лагранжа lі - суть не що інше як двоїсті змінні (двоїсті оцінки), які характеризують чутливість функції мети щодо зміни значень bi.
Приклад 7. Графічне розв’язування нелінійних задач Знайти оптимальний розв’язок таких задач: а)
б)
в)
У випадку а) максимальне значення функції мети досягається в точці В(1; 0), тобто fmax =f(B)=1. Мінімальне значення f(х) досягається в точці А(0;1) і дорівнює fmin =f(А)=-1. У випадку б) максимальне значення ФМ досягається в точці С(0; 4), тобто fmax =f(С)=(0-4)2+(4-1)2=25. Мінімальне значення f(х) досягається у внутрішній точці Е(4;1) і дорівнює fmin =f(Е)=0. У випадку в) максимальне значення ФМ досягається в точці М(7; 4/7), тобто fmax =f(М)=49+16/49=2417/49. Мінімальне значення функції мети досягається в точках А(1;4) та L(4;1) і дорівнює fmin =f(L)=17.
Приклад 8. Знаходження оптимального розв’язку нелінійної задачі за методом множників Лагранжа Для задачі
Знайти оптимальний розв’язок. Будуємо функцію Лагранжа
За необхідною умовою існування екстремуму функції Лагранжа отримаємо:
Звідки слідує:
Приклад 9. Знаходження оптимального розв’язку лінійної задачі за методом множників Лагранжа Для задачі
побудуємо функцію Лагранжа
і запишемо необхідні умови Куна-Такера існування екстремуму функції:
Пересвідчуємося, що ці умови виконуються для Х0=(6/7; 4/7) при l0=(3/7; 1/7), а значить точка Х0=(6/7; 4/7) є точкою максимуму функції мети в заданій області допустимих розв’язків. Оскільки l10=3/7, l20=1/7, то це означає, що збільшення b1 в умові задачі на одиницю (b1¢ =3) призведе до зростання функції мети на 3/7, а збільшення b2=4 на одиницю (b2¢ =5), призведе до зростання функції мети на 1/7.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.83.150 (0.029 с.) |






 (1.107)
(1.107) , (1.108)
, (1.108)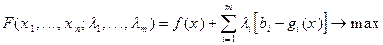 (1.109)
(1.109) (1.110)
(1.110) , (1.111)
, (1.111) , (1.112)
, (1.112) (1.113)
(1.113) (1.114)
(1.114) (1.115)
(1.115)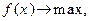 (1.116)
(1.116)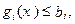 (1.117)
(1.117)
 (1.119)
(1.119) (1.120)
(1.120) (1.121)
(1.121) (1.122)
(1.122) (1.123)
(1.123)


 (1.124)
(1.124)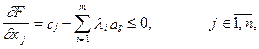 (1.125)
(1.125) (1.126)
(1.126) (1.127)
(1.127) (1.128)
(1.128)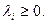 (1.130)
(1.130) (1.131)
(1.131)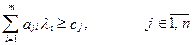 (1.132)
(1.132) (1.133)
(1.133) (1.134)
(1.134) (1.136)
(1.136) (1.137)
(1.137)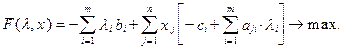 (1.138)
(1.138) (1.139)
(1.139) (1.140)
(1.140) (1.141)
(1.141) (1.142)
(1.142) (1.143)
(1.143) (1.144)
(1.144)