
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для этого определим интервалы знакопостоянства ее производной⇐ ПредыдущаяСтр 14 из 14
Этот квадратный трехчлен имеет корни x1=0, x2=2, поэтому при При
Вспомните теперь определение экстремальных точек функции. Определение. Точка x0, в которой f(x0) непрерывна, а производная функции y=f(x) равна нулю или не существует, называется критической точкой этой функции. Теорема (необходимое условие экстремума). Пусть x0 – экстремальная точка функции y=f(x), тогда x0 – критическая точка этой функции. Пример. Функция y = x3 имеет критическую точку x0=0, так как это единственное решение уравнения f ' (x)=3 x 2=0. Однако экстремальных точек у этой функции нет, y=x3 строго возрастает на всей числовой оси. Теорема (достаточное условие экстремума). Пусть функция y=f(x) непрерывна в окрестности U(x0) критической точки x0 и дифференцируема в U(x0) кроме быть может самой точке x0. Тогда 1) если в U(x0) f ' (x)>0 при х<x0 и f '(x)<0 при x>x0, то x0 ¾ точка максимума; 2) если в U(x0) f ' (x)<0 при х<x0 и f '(x)>0 при x>x0, то x0 ¾ точка минимума; 3) если в U(x0) f ' (x)>0 или f '(x)<0 при x¹ x0, то в x0 ¾ экстремума нет. Итак, чтобы определить экстремальные точки функции необходимо найти все ее критические точки и установить знаки производной в интервалах между ними. Затем согласно достаточному условию экстремума исследуются найденные критические точки. Точки непрерывности функции, где производная меняет свой знак с "плюса" на "минус", являются точками максимума; точки, где производная меняет свой знак с "минуса" на "плюс", являются точками минимума; точки, где производная свой знак не меняет, экстремальными не являются. Пример. Исследовать функцию Производная функции
не существует при x1=0.
Из уравнения
Функция
Построим теперь эскиз графика функции, учитывая, что при х®0 Приведем еще один достаточный признак экстремума, использующий вторую производную функции. Теорема. Пусть функция y=f(x) дифференцируема в некоторой окрестности критической точки х0 и f ''(x0) существует. Тогда, если Пример. Найти экстремальные точки функции y=2sinx+cos2x. В силу ее периодичности достаточно рассмотреть отрезок [0,2 f ' (x)=2cosx–2sin2x=0Þ cosx– 2sinxcosx = 0 Þ cosx(1 – 2sinx)=0. Из уравнения cosx=0 получаем Вычислим f '' (x)=–2sinx–4cos2x.
Итак, точки
С помощью исследования экстремумов можно находить наибольшее и наименьшее значение функции на отрезке. Поскольку
Аналогично
Пример Найти
f '' (–1)= –6<0 Þ x2= –1 точка максимума. Поэтому
f(-2)=1, f(3)=27-9+3=21, f(-1)=-1+3+3=5, f(1)=1-3+3=1
Выпуклость и точки перегиба Пусть функция y=f (x) дифференцируема в (a,b). Определение. Функция y=f (x) называется выпуклой вниз (вверх) в интервале (a,b), если для любого x0Î(a,b) значение функции в
Теорема. Пусть функция y=f(x) дважды непрерывно дифференцируема в (a,b). Эта функция выпукла вниз (вверх) на этом интервале тогда и только тогда, когда f ''(x)³0 (f ''(x) 1) Пусть y = f (x) выпукла вниз на (a,b), тогда yф-yk ³ 0 и f ''(c1) ³ 0. Перейдем к пределу при х
2) Пусть f '' (x) ³0, "xÎ(a,b), тогда получаем, что yф–yk³0, "x0, хÎ(a,b), т.е. эта функция выпукла вниз. Аналогично рассмотрите случай функции, выпуклой вверх. Пример. Гипербола y=1/x в интервале (0, +¥) выпукла вниз, так как Определение. Точка х0 называется точкой перегиба для функции Теорема (необходимое условие существования точки перегиба) Пусть функция y=f(x) дважды непрерывно дифференцируема в U(x0)\{x0} и непрерывна в х0. Тогда → если → Такие точки х0, в которых f (x0) непрерывна, а f "(x0)=0 или не существует, называются критическими точками второго порядка.
Пример. У функции y=x4 точка x0=0 является критической второго порядка, так как f ''(x)=12x2 и f ''(0)=0. Однако эта точка не является точкой перегиба, так как f ''(x)³0 и функция всюду выпукла вниз (лежит выше касательной). Теорема (достаточное условие существования точки перегиба). Пусть функция y=f (x) дважды непрерывно дифференцируема в U(x0)\{x0} и непрерывна в x0, где x0 – критическая точка второго порядка. Тогда, если при x<x0 и x>x0, f ''(x) имеет разные знаки, то x0 – точка перегиба этой функции. Если же при x<x0 и x>x0, знаки f ''(x) совпадают, x0 – не точка перегиба. Итак, чтобы найти точки перегиба функции, необходимо найти все ее критические точки второго порядка и исследовать каждую из них с помощью достаточного условия точки перегиба. Пример. Найти направление выпуклости и точки перегиба функции Вычислим
f ''(x) не существует при х0=0, для остальных х, f ''(x) в нуль не обращается, т.е. х0=0 – единственная критическая точка второго порядка. Для хÎ(0,+¥), f ''(x)<0, поэтому х0=0 точка перегиба с вертикальной касательной, так как f '(x) б.б. при х®0. На промежутке (-¥, 0),
Асимптоты графика функции
Определение. Прямая L называется асимптотой для кривой k, если расстояние от точки M на k до L стремится к нулю при удалении M в бесконечность (т.е. при |OM| ®¥) (рис.8).
Асимптоты графика функции y=f(x) (коротко говорят асимптоты функции) делятся на два вида:
1) вертикальные асимптоты, т.е. прямые, параллельные оси Оy, они имеют уравнения вида х=х0; 2) наклонные асимптоты, т.е. прямые, не параллельные оси Оy; они имеют уравнения вида y=kx+b. Ясно, что функция может иметь сколько угодно вертикальных асимптот и не более двух наклонных: правую и левую. Правая асимптота определяется при абсциссе х Примеры: 1. Функция y=x2 не имеет асимптот. 2. Функция y=tgx имеет бесконечное множество вертикальных асимптот вида 3. Функция y=1/x имеет вертикальную асимптоту x=0, для левой и правой ветвей гиперболы и левую и правую наклонную асимптоту y=0. 4. Функция y=|x| имеет левую наклонную асимптоту y= –x и правую y=x. Вертикальных асимптот у нее нет. Теорема (о вертикальной асимптоте). Прямая х=х0 является вертикальной асимптотой функции y=f (x) только в том случае, когда при х Геометрический смысл этой теоремы ясен. Пример. Найти вертикальные асимптоты функции Очевидно, что значения х0, определяющие вертикальные асимптоты, лежат среди точек разрыва этой функции. Таких точек две: х1= –1, x2= +1.
Поэтому функция имеет две вертикальные асимптоты х= –1, x=+1 (рис. 23).
Теорема (о наклонной асимптоте). Прямая y=kx+b является правой (левой) наклонной асимптотой функции y=f (x) в том и только том случае, когда существуют (конечные) пределы
Пример. Найти асимптоты гиперболы Эта гипербола состоит из двух графиков функций Рассмотрим случай положительного корня. Для правой асимптоты
Следовательно, правая асимптота имеет вид
Аналогично проверьте, что левая асимптота
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.79.59 (0.077 с.) |
 .
.
 и в этом промежутке функция y = x3 – 3x2 + 1 строго убывает.
и в этом промежутке функция y = x3 – 3x2 + 1 строго убывает. , f ' (x)>0 и в этих промежутках функция строго возрастает. Так как f(0)=1 и f(+2)= - 3, то эскиз графика функции имеет вид (рис.1).
, f ' (x)>0 и в этих промежутках функция строго возрастает. Так как f(0)=1 и f(+2)= - 3, то эскиз графика функции имеет вид (рис.1).

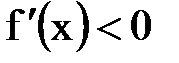

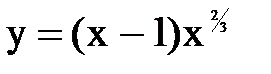 на возрастание, убывание и экстремумы.
на возрастание, убывание и экстремумы.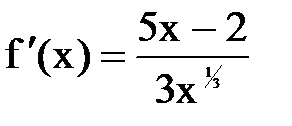
 получаем вторую критическую точку
получаем вторую критическую точку  . Методом интервалов определяем знаки f ' (x) (рис.2).
. Методом интервалов определяем знаки f ' (x) (рис.2).
 всюду непрерывна; согласно достаточному условию экстремума x1=0 есть точка максимума, а
всюду непрерывна; согласно достаточному условию экстремума x1=0 есть точка максимума, а  точка минимума. В интервалах (–¥, 0) и
точка минимума. В интервалах (–¥, 0) и  эта функция возрастает, а в интервале
эта функция возрастает, а в интервале  она убывает. Результаты исследования занесем в таблицу
она убывает. Результаты исследования занесем в таблицу )
)
 min
min
 ]. Найдем критические точки из уравнения
]. Найдем критические точки из уравнения ,
,  , а из уравнения
, а из уравнения ,
, 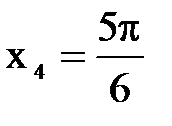 .
. ,
,  ,
,  ,
, 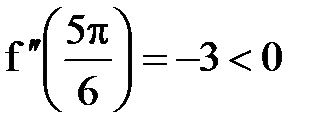 .
. ,
,  являются точками минимума, а
являются точками минимума, а  ,
,  точками максимума (kÎ Z). График этой функции имеет вид (рис.4).
точками максимума (kÎ Z). График этой функции имеет вид (рис.4).




 может достигаться или на концах отрезка [a,b] или в одной из точек максимума, то для его нахождения необходимо найти все максимумы функции в [a,b],
может достигаться или на концах отрезка [a,b] или в одной из точек максимума, то для его нахождения необходимо найти все максимумы функции в [a,b],  = max{f(a), f(b), f(xi): xiÎ(a,b) точки максимумa}.
= max{f(a), f(b), f(xi): xiÎ(a,b) точки максимумa}. = min{f(a), f(b), f(xi): xiÎ(a,b) точки минимумa}.
= min{f(a), f(b), f(xi): xiÎ(a,b) точки минимумa}. и
и  для f(x)=x3–3x+3.
для f(x)=x3–3x+3. (x)=3x2 – 3 существует для всех х. Из уравнения 3х2 – 3=0 получаем критические точки х1,2=±1, х1,2Î[–2,3], f ''(x)=6x,
(x)=3x2 – 3 существует для всех х. Из уравнения 3х2 – 3=0 получаем критические точки х1,2=±1, х1,2Î[–2,3], f ''(x)=6x, 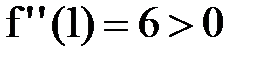 , х1=1 – точка минимума.
, х1=1 – точка минимума. = max{f (-2), f (3), f (-1)} = max{1,21,5} = 21.
= max{f (-2), f (3), f (-1)} = max{1,21,5} = 21. = min{f (-2), f (3), f (1)} = min{1,21,1} = 1.
= min{f (-2), f (3), f (1)} = min{1,21,1} = 1.










 0) "xÎ(a,b).
0) "xÎ(a,b). x0, получаем, в силу непрерывности f ''(x), что
x0, получаем, в силу непрерывности f ''(x), что
 , "x0 (0, +¥), на интервале (–¥, 0) она выпукла вверх, так как
, "x0 (0, +¥), на интервале (–¥, 0) она выпукла вверх, так как  , "xÎ (–¥, 0).
, "xÎ (–¥, 0). → точка → перегиба → то
→ точка → перегиба → то  или не существует.
или не существует.
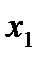



 направлена выпуклостью вниз, а на промежутке (0,+¥) она направлена выпуклостью вверх (рис.7).
направлена выпуклостью вниз, а на промежутке (0,+¥) она направлена выпуклостью вверх (рис.7).

 ,
,  и не имеет наклонных асимптот.
и не имеет наклонных асимптот. .
. ,
,  .
. и
и 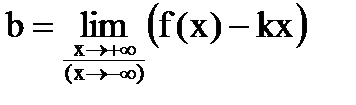 . (5.3)
. (5.3) .
. .
. =
=  =
= 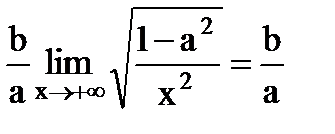
 =
= 
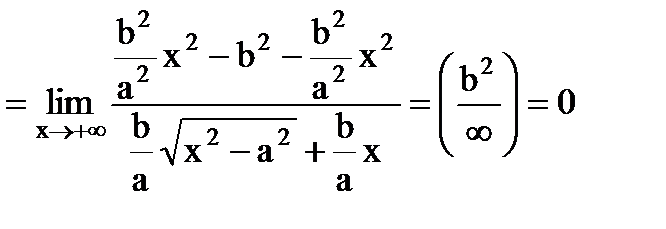 .
.






