Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение по чертежу взаимного положения прямых линийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Такое определение связано с решением позиционных и метрических задач. Прямые линии в пространстве могут занимать одно из следующих трёх возможных взаимных положений: 1. Прямые параллельны. 2. Прямые пересекаются. 2.1. Прямые пересекаются под прямым углом. 3. Прямые скрещиваются. 3.1. Прямые скрещиваются под прямым углом. 1. Определение по чертежу параллельных прямых линий (позиционные задачи)
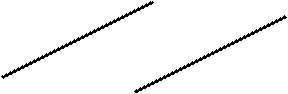
Признак параллельности прямых линий на чертеже (рис. 3.14): одноимённые проекции таких прямых - параллельны.
b
b
Рис. 3.14
2. Определение по чертежу пересекающихся прямых линий (позиционные задачи) Признак пересекающихся прямых на чертеже (рис.3.15): точки пересечения одноимённых проекций пересекающихся прямых лежат на одной линии связи, являясь проекциями точки пересечения этих прямых.
a
Рис. 3.15
2.1. Определение по чертежу перпендикуляно пересекающихся прямых (комплексные задачи)
Определение таких прямых базируется на признаке пересекающихся прямых (позиционная задача) и на свойстве проецирования прямого угла (ОМЗ-2): прямой угол проецируется на плоскость без искажения только в том случае, если хотя бы одна из его сторон параллельна этой плоскости.
Признак перпендикулярно пересекающихся прямых (рис. 3.16): если одна из перпендикулярно пересекающихся прямых является прямой уровня, то на плоскости проекций, которой она параллельна, прямой угол изображается без искажения.
b h
Рис. 3.16
3. Определение по чертежу скрещивающихся прямых (позиционные задачи)
Признак скрещивающихся прямых на чертеже (рис. 3.17): точки пересечения одноимённых проекций скрещивающихся прямых не лежат на одной линии связи, а являются слиянием двух проекций конкурирующих точек этих прямых.
a
B
Рис. 3.17
4. Определение по чертежу перпендикулярно скрещивающихся прямых (комплексные задачи).
Признак перпендикулярно скрещивающихся прямых на чертеже (рис. 3.18): если одна из перпендикулярно скрещивающихся прямых параллельна какой-либо плоскости проекций, то на этой плоскости угол между их проекциями остаётся без искажения прямым.
h
Рис. 3.18
Примеры решения задач о взаимном положении прямых
Задача 1 (рис. 3.19а). Определить взаимное положение отрезков АВ и CD, если заданы их горизонтальные и фронтальные проекции.
B
A
а) б) Рис. 3.19
Решение задачи (рис. 3.19б) Так как заданные отрезки принадлежат профильным прямым, то построим профильные проекции этих отрезков, которые показывают, что заданные прямые линии скрещиваются.
Задача 2 (рис. 3.20а). Заданную прямую a пересечь фронталью f, проходящей через точку M.
N
a а) б) Рис. 3.20 Решение задачи ( рис. 3.20б ) 1. M 2. N Задача 3 (рис. 3.21а). Задан чертёж прямой линии общего положения a и фронтальная проекция точки М. Провести через эту точку горизонталь h так, чтобы h
M
N а) б) Рис. 3.21
Решение задачи ( рис. 3.21б ) 1. М 2. N
Задача 4 (рис. 3.22а). Заданы профильно конкурирующие точки А и В, через которые проходят взаимно перпендикулярные прямые a и h. Построить недостающие проекции этих прямых.
A
а) б) Рис. 3.22
Решение задачи ( рис. 3.22б ). 1. В 2. a
Вопросы для самоконтроля 1. Какие прямые линии относят к прямым частного положения? 2. Какие проекции прямых уровня называют определяющими проекциями? 3. Какие проекции проецирующих прямых называют главными проекциями? 4. На какой плоскости проекций прямая уровня изображается в истинную величину? 5. На каких плоскостях проекций углы наклона к ним прямых уровня изображаются без искажения? 6. Назвать метод определения длины отрезка прямой общего положения и углов его наклона к плоскостям проекций? Объяснить дополнительные построения, связанные с этим методом? 7. Назвать признак параллельных прямых на чертеже. 8. Назвать признак пересекающихся прямых на чертеже. 9. Назвать признак перпендикулярно пересекающихся прямых на чертеже. 10. Назвать признак скрещивающихся прямых на чертеже. 11. Назвать признак перпендикулярно скрещивающихся прямых на чертеже.
Кривые линии на чертеже
Кривая линия, как и прямая, это простейшая геометрическая фигура (элемент моделирования), которую можно представить, как траекторию непрерывного движения точки по определённому закону. Построение кривых линий на чертеже производят с помощью достаточно большого числа её точек. Различают плоские и пространственные кривые линии. Чтобы определить по чертежу вид кривой, необходимы дополнительные построения (рис. 4.1). Если на заданной кривой m взять 4 произвольные точки A, B, C, D, то, соединив эти точки хордами АС и BD, можно получить 2 варианта.
A
B
A C B Рис. 4.1
1-й вариант. Хорды пересекаются. Это значит, что они образуют плоскость, в которой лежит заданная кривая, т.е. эта кривая - плоская. 2-й вариант. Хорды не пересекаются, а скрещиваются. Это значит, что заданная кривая пространственная. В нашем примере кривая – пространственная.
Среди пространственных кривых широко известна в машиностроении цилиндрическая винтовая линия (рис. 4.2). Она моделируется траекторией непрерывного сложного движения образующей точки: вращательного (при постоянном радиусе и скорости) и поступательного параллельно оси вращения (тоже с постоянной скоростью). Расстояние, на которое переместится образующая точка вдоль оси вращения за один оборот, называют ходом винтовой линии.
B
B
1
Рис.4.2
Примером плоских кривых линий являются: окружность, эллипс,парабола, гипербола. Эти кривые описываются уравнениями второго порядка и поэтому их называют кривые второго порядка. Плоские кривые (рис. 4.3), составленные из нескольких сопрягаемых дуг кривых линий различных уравнений называют обводами (обводы корпуса корабля, яхты, лодки).
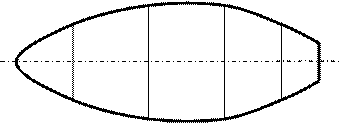
Рис. 4.3. Обводы судна
Если плоские кривые линии составлены из сопряжённых дуг окружностей различных радиусов, то их называют коробовыми. Решим задачу (рис. 4.4): через заданные точки A, B, C, D провести коробовую линию.
B
Рис. 4.4. Коробовая линия
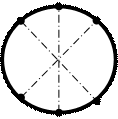
Замкнутые коробовые кривые линии, имеющие не более двух точек пересечения с произвольной прямой, называются овалами (рис. 4.5).
r R O Рис. 4.5. Овал
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 1822; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 ||a
||a  a
a 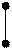 B
B  B
B 
 a
a 
 M
M 
 a
a 
 b
b 

 A
A 

 A
A 

 B
B 

 a
a  b
b 
 b
b 
 a
a 

 h
h 







 A
A  C
C 




 B
B 

 a
a 

 M
M 


 M
M 
 f
f  л.с., f
л.с., f  a
a 
 h
h 




 a
a 




 a
a 
 M
M 
 a
a 

 h
h 
 a
a 
 h
h 
 A
A 





 D
D 
 D
D 





 Ход
Ход

 1
1 



 A
A 







 A C D
A C D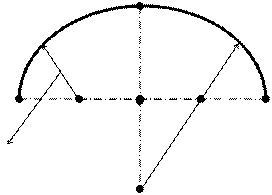
 O
O