
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие фазового пространства и фазовой траектории. Автономные системы ОДУ, св-ва их фазовых траекторий. ⇐ ПредыдущаяСтр 7 из 7
Считается, что Пусть Кривая Г: -интегральная кривая системы (6) Гс Определение. Пространство Определение. Если функции То система ОДУ называется автономной Определение. Точка Свойства фазовых траекторий автономной системы 1) Если точка Док-во: 2) Если Док-во: Замечание: Точка покоя 3) Если фазовая траектория отлична от точки покоя, то она является гладкой кривой(т.е. в каждой её точке 4) Если 5) 6)
36. Исследование устойчивости положения покоя системы двух ЛДУ с постоянными коэффициентами в случае
Находим точки покоя
I) II) (x0,y0) — точка прямой III)
I) 1°
37. Исследование устойчивости положения покоя системы двух ЛДУ с постоянными коэффициентами в случае
Точки покоя:
det(A-λE) = 0
1)
Решение периодично T=
x(t)=x(t+T) y(t)=y(t+T) Все фазовые траектории замкнуты
Система асимптотически устойчива; фазовые траектории: спирали, накрученные на точку покоя
Устойчивый фокус
а)
спирали
Неустойчивый фокус 38. Исследование устойчивости положения покоя системы двух ЛДУ с постоянными коэффициентами в случае
Точки покоя:
det(A-λE) = 0
1) Матрица А имеет 1 линейно независимый собственный вектор (к
а) асимптоти-чески устойчивая система
Устойчивый вырожденный узел б)
|
|||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.195 (0.022 с.) |
 =
=  (6)
(6)  =
=  i=1,…,n
i=1,…,n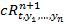
 =
=  (t), t
(t), t 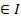 –решение системы (6)
–решение системы (6) –
–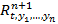 – пространство решений
– пространство решений называется фазовым пространством системы (6), а кривая
называется фазовым пространством системы (6), а кривая  , задаваемая направлением
, задаваемая направлением 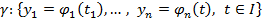 , где
, где 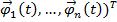 - решение системы (5), называется фазовой траекторией системы (5).
- решение системы (5), называется фазовой траекторией системы (5). не зависят явно от
не зависят явно от  , т.е. система имеет вид (7)
, т.е. система имеет вид (7) 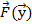 ;
; 
 =(
=( ,…,
,…,  называется точкой покоя (положением равновесия) автономной системы (7), если
называется точкой покоя (положением равновесия) автономной системы (7), если  , т.е.
, т.е. 
 -точка покоя системы (7), то вектор-функция
-точка покоя системы (7), то вектор-функция  (t)
(t)  является решением системы (7)
является решением системы (7) =
=  =
=  =f(
=f( (t)
(t) 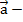 точка покоя системы (7), то
точка покоя системы (7), то  – фазовая траектория системы (7)
– фазовая траектория системы (7) - решение (7)
- решение (7)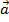 называется (ассимтотически) устойчивой или неустойчивой, если устойчиво или (ассимтотически устойчиво или неустойчиво) решение
называется (ассимтотически) устойчивой или неустойчивой, если устойчиво или (ассимтотически устойчиво или неустойчиво) решение  ненулевой касательный вектор).
ненулевой касательный вектор). вектор-функция
вектор-функция  2 фазовые траектории либо не пересекаются, либо совпадают.
2 фазовые траектории либо не пересекаются, либо совпадают. следующие типы фазовых траекторий: 1. Точка (положение равновесия); 2.гладкая замкнутая кривая (цикл); 3.гладкая кривая без точек самопересечения;
следующие типы фазовых траекторий: 1. Точка (положение равновесия); 2.гладкая замкнутая кривая (цикл); 3.гладкая кривая без точек самопересечения;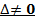 ,
,  - действительные.
- действительные.

 ,
, 

 — вектор скорости
— вектор скорости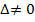 — единственная точка покоя (0,0)
— единственная точка покоя (0,0)

 — все точки плоскости есть точки покоя.
— все точки плоскости есть точки покоя.
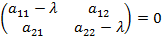 — характеристическое уравнение
— характеристическое уравнение — корни
— корни
 ,
, 

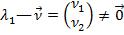
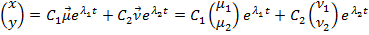 — общее решение
— общее решение A=
A= 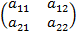 ,
, ;
; 
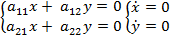 ,
, 
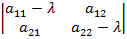 =0 – характеристическое уравнение.
=0 – характеристическое уравнение.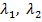 – корни характеристического уравнения.
– корни характеристического уравнения.

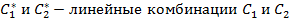
 =0,
=0,  ,
,  ,
, 
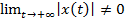 , т.е. нулевоереш. не явл. асимптотически уст.
, т.е. нулевоереш. не явл. асимптотически уст.
 Центр (нет асимптотической устойчивости)
Центр (нет асимптотической устойчивости)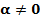 а)
а) 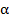 =Re
=Re  ,
,  ,
, ,
, Система неустойчива; фазовые траектории: раскрученные
Система неустойчива; фазовые траектории: раскрученные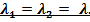
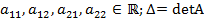
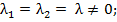 кратные корни
кратные корни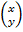 =
= 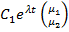 +
+ 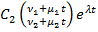
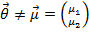 -собственный вектор, отвечающий
-собственный вектор, отвечающий 
 )
)
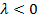
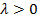 неустойчивая система
неустойчивая система


