
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории массового обслуживания.
Таким образом, общая функциональная схема СМО будет иметь вид:
Рис.4.2. Функциональная схема СМО. Здесь: l - интенсивность входного потока. m - интенсивность выходного потока заявок. Размерность
Поток заявок Пуассона. Определение: Если поток заявок стационарен, ординарен и не имеет последствия, то он называется простейшим потоком или потоком Пуассона. Поток заявок называется стационарным, если вероятность попадания числа заявок на участок времени длиной t зависит только от длины участка, а не от места где он расположен. Т.е распределение заявок во времени равномерное. Поток заявок называется ординарным, если вероятность попадания на бесконечно малый участок Dt двух и более заявок мала по сравнению с вероятностью попадания одной заявки. Поток называется без последствия, если число заявок, попадающих на один участок, не зависит от числа заявок, попадающих на другие участки. (участки не Перекрываются) Для потока Пуассона вероятность поступления за время t ровно m заявок:
Вывод о том, что принятый процесс с достаточной вероятностью описывается пуассоновским распределением, проверяются по критерию Х2. Расчётное значение: где Для числа степеней свободы r=k-2 и величина Х2 определяют вероятность P. Если Марковские процессы. Процессы массового обслуживания являются дискретными процессами с конечным числом состояний и непрерывным временем. Переход из одного состояния в другое происходит в момент, когда наступают какие-то события, вызывающие такой переход (поступление нового требования, начало или конец обслуживания, уход требования из очереди). Будущее состояние процесса зависит только от состояния в настоящий момент и не зависит от того, как происходило развитие процесса в прошлом. Такие процессы называются марковскими.
Рис.4.3. Граф состояний. Зафиксируем момент t и найдём вероятность Pk(t+Dt) того, что в момент t+Dt система будет в состоянии Sk. Так как система может оставаться в прежнем состоянии или переходить только в соседнее состояние, то Pk(t+Dt)=P(A)+P(B)+P(C), где А,В,С – несовместимые события. Событие А означает, что система за время Dt не изменила своего состояния Sk, а события В и С означают, что переход в Sk произошёл соответственно из состояний Sk-1 и Sk+1. Пусть система в момент t находилась в состоянии Si и вероятность того, что за время Dt она перейдёт в состояние Sj равна Pij(Dt). Величину Очевидно, вероятность того, что система за время Dt не перейдёт из состояния i в состояние j выражается как: Выразим вероятностb событий А,В,С через вероятности состояний и плотности вероятностей перехода. (членам Dt2, высших порядков малости по сравнению с Dt пренебрежем). 1-Pk,k-1(t) 1-Pk,k+1(t)
P(A)»Pk(t)(1-lk,k-1Dt)(1-lk,k+1Dt)»Pk(t)[1-(lk,k-1+lk,k+1)Dt] (4.4) P(B)»Pk-1(t)lk-1,kDt, где (lk–1,kDt)=P(k-1),k (4.5) P(C)»Pk+1(t)lk+1,kDt, где (lk-+1,kDt)=P(k+1),k (4.6)
На основании этих соотношений имеем: Pk(t+Dt)=Pk(t)[1-(lk,k-1+lk,k+1)Dt]+Pk-1(t) lk-1,kDt+Pk+1(t) lk+1,kDt (4.7)
или:
Переходя к пределу при Dt®0, получим:
Анологично записываются дифференциальные уравнения для вероятностей других состояний системы и получают систему дифференциальных уравнений вероятностей состояний системы массового обслуживания. Существует правило, согласно которому дифференциальное уравнение вероятности состояния возможно записать непосредственно по графу системы. Производная вероятности k-го состояния равна алгебраической сумме членов каждый из которых представляет собой произведение веса дуги инцидентной k–той вершине на вероятности k-го, (k+1)-го, (k-1)-го состояний, причём вес дуги берётся положительным, если дуга входит в k-е состояние и отрицательным, если дуга выходит из k-го состояния. Полученную систему уравнений называют системой дифференциальных уравнений Колмогорова. При системном анализе поведения сложных объектов или процессов, часто исследуют предельное или стационарное состояние системы при t®¥. В этом случае все
производные
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.108.54 (0.009 с.) |

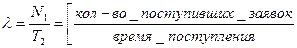 ]
]
 и
и 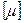 будет
будет  . Если
. Если 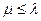 , то в СМО будут очереди, такое СМО называется с ожиданием.
, то в СМО будут очереди, такое СМО называется с ожиданием. (4.1)
(4.1) (4.2)
(4.2) ; mi – количество заявок поступивших в пределах одного интервала времени Dt; всё время делится на k интервалов, где i=1,2, … k; n – общее количество заявок.
; mi – количество заявок поступивших в пределах одного интервала времени Dt; всё время делится на k интервалов, где i=1,2, … k; n – общее количество заявок.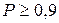 , то гипотезу о Пуассоновском законе распределения заявок можно признать правдоподобной.
, то гипотезу о Пуассоновском законе распределения заявок можно признать правдоподобной. Марковский процесс может быть представлен графически графом состояний.
Марковский процесс может быть представлен графически графом состояний. (4.3) называют плотностью вероятности перехода. При достаточно малом Dt имеет место, приближенное соотношение:
(4.3) называют плотностью вероятности перехода. При достаточно малом Dt имеет место, приближенное соотношение:  .
. .
.
 (4.8)
(4.8) (4.9)
(4.9) и система дифференциальных уравнений превращается в систему алгебраических уравнений, которая может быть решена относительно неизвестных вероятностей состояний Pk.
и система дифференциальных уравнений превращается в систему алгебраических уравнений, которая может быть решена относительно неизвестных вероятностей состояний Pk.


