
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление определителей второго порядка.Стр 1 из 5Следующая ⇒
Сложение матриц Складывать можно только матрицы одинакового размера. Сложение матриц
Свойства сложения матриц: 1. 1.коммутативность: A+B = B+A; 2. 2.ассоциативность: (A+B)+C =A+(B+C); 3. 3.сложение с нулевой матрицей: A + Θ = A; 4. 4.существование противоположной матрицы: A + (-A) = Θ;
Умножение матриц Умножение матриц (обозначение:
Количество столбцов в матрице Свойства умножения матриц: a. 1.ассоциативность (AB)C = A(BC); b. 2.некоммутативность (в общем случае): AB c. 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA; d. 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC; e. 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);
Линейные комбинации В векторном пространстве линейной комбинацией векторов
где
Это позволяет описать произведение
Теорема Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ. 1. Если столбцы В самом деле, из равенств
2. Если ранг матрицы однородной системы равен Действительно, по формулам (5.13) общего решения однородной системы найдем
которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние Любая совокупность 14 Минор Минором порядка k матрицы А называется детерминант некоторой ее квадратной подматрицы порядка k. В матрице А размеров m x n минор порядка r называется базисным, если он отличен от нуля, а все миноры большего порядка, если они существуют, равны нулю. Столбцы и строки матрицы А, на пересечении которых стоит базисный минор, называются базисными столбцами и строками А. Теорема 1. (О ранге матрицы). У любой матрицы минорный ранг равен строчному рангу и равен столбцовому рангу. Теорема 2.(О базисном миноре). Каждый столбец матрицы раскладывается в линейную комбинацию ее базисных столбцов. Рангом матрицы (или минорным рангом) называется порядок базисного минора или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Ранг нулевой матрицы по определению считают 0. Отметим два очевидных свойства минорного ранга. 1) Ранг матрицы не меняется при транспонировании, так как при транспонировании матрицы все ее подматрицы транспонируются и миноры не меняются. 2) Если А’-подматрица матрицы А, то ранг А’ не превосходит ранга А, так как ненулевой минор, входящий в А’, входит и в А. 15. Понятие
Упорядоченная совокупность n действительных или комплексных чисел Числа Два (ненулевых) вектора a и b равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны. Сложение векторов. Для сложения векторов есть два способа.1. Правило параллелограмма. Чтобы сложить векторы 2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы Вычитание векторов. Вектор Умножение вектора на число При умножении вектора Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. Если векторы перпендикулярны, их скалярное произведение равно нулю. Сложение матриц Складывать можно только матрицы одинакового размера. Сложение матриц
Свойства сложения матриц: 1. 1.коммутативность: A+B = B+A; 2. 2.ассоциативность: (A+B)+C =A+(B+C); 3. 3.сложение с нулевой матрицей: A + Θ = A; 4. 4.существование противоположной матрицы: A + (-A) = Θ;
Умножение матриц Умножение матриц (обозначение:
Количество столбцов в матрице Свойства умножения матриц: a. 1.ассоциативность (AB)C = A(BC); b. 2.некоммутативность (в общем случае): AB c. 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA; d. 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC; e. 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);
Линейные комбинации В векторном пространстве линейной комбинацией векторов
где
Это позволяет описать произведение
Вычисление определителей второго порядка. Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:
Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.
Вычисление определителей третьего порядка.
Основные свойства определителей: 1. Опр-ль не изменится при замене всех его строк столбцами с теми же номерами. 2. Опр-ль изменит знак на противоположный, если переставить местами любые 2 строки(2 столбца) определителя. 3. Общий множитель элементов какой-либо строки(столбца) можно вынести за знак определителя. 4. Опр-ль равен нулю, если содержит нулевую строку(столбец), две одинаковые или противоположные строки(столбца). 5. Опр-ль не изменится, если к какой-либо строке(столбцу)прибавить другую строку(столбец) умноженное на любое число. 6. Опр-ль треугольного вида равен произведению диагональных элементов.
7.Метод Крамера для решения СЛАУ и условия их применимости ТЕОРЕМА КРАМЕРА. Если определитель
Если 8 Метод Гаусса решения СЛАУ и условия его применимости. Условия несовместности, определённости и неопределённости СЛАУ по методу Гаусса. метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Достоинства метода:
a) менее трудоёмкий по сравнению с другими методами; b) позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение; c) позволяет найти максимальное число линейно независимых уравнений – ранг матрицы системы. Существенным недостатком этого метода является невозможность сформулировать условия совместности и определенности системы в зависимости от значений коэффициентов и свободных членов. С другой стороны, даже в случае определенной системы этот метод не позволяет найти общие формулы, выражающие решение системы через ее коэффициенты и свободные члены, которые необходимо иметь при теоретических исследованиях. 9 Преобразования СЛАУ, выполняемые методом Гаусса (можно на примере). Нахождение общего решения СЛАУ. Частные решения СЛАУ.
1) из элементов строки 2 вычитаем элементы строки 1, умноженные на 2;
10 Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы. Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E: A·A-1 = A-1·A = E Квадратная матрица А называется невырожденной, если определитель Δ=detА не равен нулю:Δ=detА≠0. В противном случае (Δ=0) матрица А называется вырожденной. квадратная матрица называется вырожденной, если строки линейно зависимы. Вырожденной будет, например, матрица, имеющая две одинаковые строки. Примером невырожденной матрицы является единичная матрица. Матрица А-1 называется обратной матрице А, если выполняется условие A*A-1=A-1*A=E где Е — единичная матрица того же порядка, что и матрица A. Матрица А-1 имеет те же размеры, что и матрица А.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.140.5 (0.053 с.) |
 есть операция нахождения матрицы
есть операция нахождения матрицы  , все элементы которой равны попарной сумме всех соответствующих элементов матриц
, все элементы которой равны попарной сумме всех соответствующих элементов матриц  и
и  , то есть каждый элемент матрицы
, то есть каждый элемент матрицы 
 , реже со знаком умножения
, реже со знаком умножения  ) — есть операция вычисления матрицы
) — есть операция вычисления матрицы 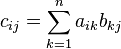
 ,
,  , то размерность их произведения
, то размерность их произведения  есть
есть  .
. BA;
BA; называется вектор
называется вектор
 — коэффициенты разложения:
— коэффициенты разложения: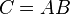 матриц
матриц  — решения однородной системы уравнений, то любая их линейная комбинация
— решения однородной системы уравнений, то любая их линейная комбинация  также является решением однородной системы.
также является решением однородной системы. следует, что
следует, что , то система имеет
, то система имеет  линейно независимых решений.
линейно независимых решений.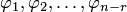 , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):
, придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

 -ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы.
-ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.
-мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов. называется n-мерным вектором.
называется n-мерным вектором. и
и  , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов
, помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов  направлен противоположно вектору
направлен противоположно вектору  . Длины векторов
. Длины векторов  .
.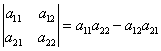
 +
+  +
+  -
-  -
-  -
- 
 системы
системы  линейных алгебраических уравнений с
линейных алгебраических уравнений с  то эта система имеет единственное решение, которое находится по формулам Крамера:
то эта система имеет единственное решение, которое находится по формулам Крамера:
 - определители, образованные с
- определители, образованные с  -го столбца, столбцом из свободных членов.
-го столбца, столбцом из свободных членов. , а хотя бы один из
, а хотя бы один из  отличен от нуля, то СЛАУ решений не имеет. Если же
отличен от нуля, то СЛАУ решений не имеет. Если же  , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.
, то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.
 , откуда находим
, откуда находим  .
. , откуда находим
, откуда находим  .
.
 , или
, или  .
. где
где  и
и  - свободные переменные.
- свободные переменные.


