Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой этой плоскости.

Прямая принадлежит плоскости, если две ее точки принадлежат плоскости.

Эти два вполне очевидных предложения часто называют условиями принадлежности точки и прямой плоскости.

На рис. 3.6 плоскость общего положения задана треугольником АВС. Точки А, В, С принадлежат этой плоскости, так как являются вершинами треугольника из этой плоскости. Прямые (АВ), (ВС), (АС) принадлежат плоскости, так как по две их точки принадлежат плоскости. Точка N принадлежит (AC), D принадлежит (AB), E принадлежит (CD) и, значит, точки N и E принадлежат плоскости (DABC), тогда прямая (NE) принадлежит плоскости (DABC).

Если задана одна проекция точки L, например L₂, и известно, что точка L принадлежит плоскости (DABC), то для нахождения второй проекции L₁ последовательно находим (A₂L₂), K₂, (A₁K₁), L₁.

Если условие принадлежности точки плоскости нарушено, то точка не принадлежит плоскости. На рис. 3.6 точка R не принадлежит плоскости (DABC), так как R₂ принадлежит (F₂K₂), а R₁ не принадлежит (A₁K₁).

На рис. 3.7 приведен комплексный чертеж горизонтально проецирующей плоскости (DCDE). Точки K и P принадлежат этой плоскости, так как P₁ и K₁ принадлежат прямой (D₁C₁), являющейся горизонтальной проекцией плоскости (DCDE). Точка N не принадлежит плоскости, так как N₁ не принадлежит (D₁C₁).

Все точки плоскости (DCDE) проецируются на П₁ в прямую (D₁C₁). Это следует из того, что плоскость (DCDE) ^ П₁. В этом же можно убедиться, если проделать для точки P (или любой другой точки) построения, которые были сделаны для точки L (рис. 3.6). Точка P₁ попадет на прямую (D₁C₁). Таким образом, для того, чтобы определить принадлежность точки горизонтально проецирующей плоскости, фронтальная проекция (DC₂D₂E₂) не нужна. Поэтому в дальнейшем проецирующие плоскости будут задаваться только одной проекцией (прямой линией). На рис. 3.7 показана фронтально проецирующая плоскость S, заданная фронтальной проекцией S₂, а также точки A Î S и B Ï S.

Взаимное положение точки и плоскости сводится к принадлежности или не принадлежности точки плоскости.

При решении многих задач приходится строить линии уровня, принадлежащие плоскостям общего и частного положения. На рис. 3.8 показаны горизонталь h и фронталь f, принадлежащие плоскости общего положения (DABC). Фронтальная проекция h₂ параллельна оси x, поэтому прямая h – горизонталь. Точки 1 и 2 прямой h принадлежат плоскости, поэтому прямая h принадлежит плоскости. Таким образом, прямая h – это горизонталь плоскости (DABC). Обычно порядок построения такой: h₂; 1₂, 2₂; 1₁, 2₁; (1₁2₁) = h₁. Фронталь f проведена через точку A. Порядок построения: f₁ // x, A₁Î f₁; 3₁, 3₂; (A₂3₂) = f₂.

На рис. 3.9 показаны проекции горизонтали и фронтали для фронтально проецирующей плоскости S и горизонтально проецирующей плоскости Г. В плоскости S горизонталь является фронтально проецирующей прямой и проходит через точку A (попытайтесь представить горизонталь как линию пересечения S и плоскости, проходящей через точку A параллельно П₁). Фронталь проходит через точку С. В плоскости Г горизонталь и фронталь проведены через одну точку D. Фронталь является горизонтально проецирующей прямой.

Из рассмотренных выше построений следует, что линию уровня в плоскости можно провести через любую точку этой плоскости.

Совпадение плоскостей можно трактовать как принадлежность одной плоскости другой. Если три точки одной плоскости принадлежат другой плоскости, то эти плоскости совпадают. Упомянутые три точки не должны лежать на одной прямой. На рис. 3.10 плоскость (DDNE) совпадает с плоскостью S(DABC), так как точки D, N, E принадлежат плоскости S(DABC).

Обратим внимание на то, что плоскость S, заданная DABC, теперь может быть задана DDNE. Любая плоскость может быть задана линиями уровня. Для этого необходимо через точку плоскости S(DABC) (например, через точку А) провести в плоскости горизонталь и фронталь, которые и будут задавать плоскость S (на рис. 3.10 построения не показаны). Последовательность построения горизонтали: h₂ // x (A₂ Î h₂); K₂ = h₂ Ç B₂C₂; K₁ Î B₁C₁ (K₂K₁ ^ x); A₁K₁ = h₁. Последовательность построения фронтали: f₁ // x (A₁ Î f₁); L₁ = f₁ Ç B₁C₁; L₂ Î B₂C₂ (L₁L₂ ^ x); A₂L₂ = f₂. Можно записать S(DABC) = S(h, f).

 

ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА

 

В курсе начертательной геометрии под преобразованием комплексного чертежа фигуры обычно понимается его изменение, вызванное перемещением фигуры в пространстве, или введением новых плоскостей проекций, или использованием других видов проецирования. Применение различных методов (способов) преобразования комплексного чертежа упрощает решение многих задач.

 

4.1. Метод замены плоскостей проекций

 

Метод замены плоскостей проекций состоит в том, что вместо одной из плоскостей проекций вводится новая плоскость, перпендикулярная к другой плоскости проекций. На рис. 4.1 показана пространственная схема получения комплексного чертежа точки А в системе (П₁П₂). Точки А₁ и А₂ – горизонтальная и фронтальная проекции точки А, АА₁А_xА₂ – прямоугольник, плоскость которого перпендикулярна оси x (рис. 2.3).

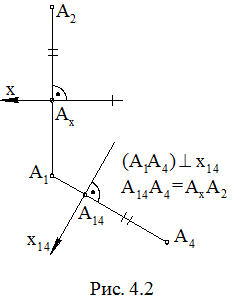Новая плоскость П₄ перпендикулярна П₁. При проецировании точки А на П₄ получим новую проекцию А₄, фигура АА₁А₁₄А₄ – прямоугольник, плоскость которого перпендикулярна новой оси x₁₄ = П₄ Ç П₁. Для получения комплексного чертежа будем рассматривать фигуры, расположенные в плоскостях проекций. Поворотом вокруг оси x₁₄ совместим П₄ с П₁, затем поворотом вокруг оси x совместим П₁ (и П₄) с П₂ (на рис. 4.1 направления движения плоскостей П₄ и П₁ показаны штриховыми линиями со стрелками). Полученный чертеж приведен на рис. 4.2. Прямые углы на рис. 4.1, 4.2 помечены дугой с точкой, равные отрезки помечены двумя штрихами (противоположные стороны прямоугольников на рис. 4.1). От комплексного чертежа точки А в системе (П₁П₂) перешли к комплексному чертежу точки А в системе (П₁П₄), заменили плоскость П₂ на плоскость П₄, заменили А₂ на А₄.

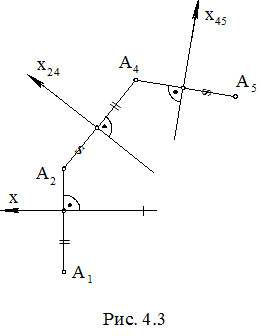На основе этих построений сформулируем правило замены плоскостей проекций (правило получения новой проекции). Через незаменяемую проекцию проводим новую линию проекционной связи перпендикулярно новой оси, затем от новой оси по линии проекционной связи откладываем отрезок, длина которого равна расстоянию от заменяемой проекции до старой оси, полученная при этом точка и есть новая проекция. Направление новой оси будем брать произвольно. Новое начало координат указывать не будем.

На рис. 4.3 показан переход от комплексного чертежа в системе (П₁П₂) к комплексному чертежу в системе (П₂П₄), а затем еще один переход к комплексному чертежу в системе (П₄П₅). Вместо плоскости П₁ введена плоскость П₄, перпендикулярная П₂, затем вместо П₂ введена плоскость П₅, перпендикулярная П₄. Используя правило замены плоскостей проекций, можно выполнить любое количество замен плоскостей проекций.