
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ж) если один угол в треугольнике прямой, то треугольник будет тупоугольным.Стр 1 из 7Следующая ⇒
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания. Алгебра логики определяет правила выполнения операций с логическими величинами, которые могут быть равны только 0 или 1, то есть с двоичными данными. Используя эти правила, можно строить элементы памяти и выполнять арифметические действия. Высказывания бывают простые и сложные. Простые высказывания нельзя разделить на более мелкие высказывания, например: “Сейчас идет дождь” или “Форточка открыта”. Сложные (составные) высказывания строятся из простых с помощью логических связок (операций) “И”, “ИЛИ”, “НЕ”, “если…, то”, “тогда и только тогда”. В булевой алгебре высказывания обычно обозначаются латинскими буквами. Таким образом, мы уходим от конкретного содержания высказываний, нас интересует только их истинность или ложность. Например, можно обозначить буквой A высказывание “Сейчас идет дождь”, а буквой B — высказывание “Форточка открыта”. Из них строятся сложные высказывания: не A: “Сейчас нет дождя”. не B: “Форточка закрыта”. A и B: “Сейчас идет дождь, и открыта форточка”. A или B: “Сейчас идет дождь, или открыта форточка”. если A, то B: “Если сейчас идет дождь, то форточка открыта”. Операции “НЕ”, “И” и “ИЛИ” используются чаще других. Оказывается, с их помощью можно выразить любую логическую операцию, поэтому эти три операции можно считать основными, базовыми. Операция «НЕ» Операция “НЕ” часто называется отрицанием, или инверсией. В алгебре логики всего два знака, 0 и 1, поэтому логическое отрицание — это переход от одного значения к другому, от 1 к 0 или наоборот. Если высказывание A истинно, то “не А ” ложно, и наоборот. Для обозначения операции “НЕ” используются несколько способов. Выражение “не А” в алгебре логики записывается как Операцию “НЕ” можно задать в виде таблицы:
Эта таблица состоит из двух частей: слева перечисляются все возможные значения исходного высказывания (их всего два — 0 и 1), а в последнем столбце записывают результат выполнения логической операции для каждого из этих вариантов. Такая таблица называется таблицей истинности логической операции.
Таблица истинности задает логическую функцию, то есть правила преобразования входных логических значений в выходные. Операция «И» Пусть есть два высказывания: A — “Сейчас идет дождь”, B — “Форточка открыта”. Сложное высказывание “ A и B ” выглядит так: “Сейчас идет дождь, и форточка открыта”. Оно будет истинным (верным) в том и только в том случае, когда оба высказывания, A и B, истинны одновременно. Для понимания операции “И” можно представить себе простую схему, в которой для включения Чтобы лампочка загорелась, нужно обязательно включить оба выключателя. С другой стороны, чтобы выключить лампочку, достаточно выключить любой из них. Операция “И” (в отличие от “НЕ”) выполняется с двумя логическими значениями, которые мы обозначим как A и B. Результат этой операции в алгебре логики записывают как А ⋅ B, А ∧ B или А & B. В языках программирования используют обозначения “ A and B ” (Паскаль, Бейсик) или “ A && B ” (Си).
В таблице истинности будет уже не один столбец с исходными данными, а два. Число строк также выросло с 2 до 4, поскольку для 2 бит мы получаем 4 разных комбинации: 00, 01, 10 и 11. Эти строчки расположены в определенном порядке: двоичные числа, полученные соединением битов A и B, идут в порядке возрастания (слева от таблицы они переведены в десятичную систему). Как следует из определения, в последнем столбце будет всего одна единица, для варианта A = B = 1. Легко проверить, что этот результат можно получить “обычным” умножением A на B, поэтому операцию “И” называют логическим умножением. Существует и другое название этой операции — конъюнкция (от лат. conjunctio — союз, связь). Операция «ИЛИ» Высказывание “Сейчас идет дождь, или форточка открыта” истинно тогда, когда истинно хотя бы одно из входящих в него высказываний, или оба одновременно. В алгебре логики операция “ИЛИ” обозначается как А+B или А ∨ B, в языках программирования — “ A or B ” (Паскаль, Бейсик) или “ A || B ” (Си).
В таблице истинности будет только один ноль, для варианта A = B = 0. Операцию “ИЛИ” называют логическим сложением, потому что она похожа на обычное математическое сложение. Единственное отличие — в последней строке таблицы истинности: в математике 1 + 1 равно 2, а в алгебре логики — 1. Другое название операции “ИЛИ” — дизъюнкция (от лат. disjunctio — разделение). Для обозначения операций “И” и “ИЛИ” мы будем использовать знаки умножения и сложения (например, А ⋅ B и А+B). Это очень удобно потому, что они привычны для нас и позволяют легко увидеть аналогию с обычной математикой. Доказано, что операций “НЕ”, “И” и “ИЛИ” достаточно для того, чтобы записать с их помощью любую логическую операцию, которую только можно придумать. Например, для двух переменных существует всего 24 = 16 логических операций: их таблицы истинности отличаются только последним столбцом, в котором 4 двоичных значения (4 бита). Далее мы рассмотрим еще три распространенных операции и покажем, как их можно представить через операции “НЕ”, “И” и “ИЛИ”. Операция “исключающее ИЛИ” Операция “исключающее ИЛИ” отличается от обычного “ИЛИ” только тем, что результат равен 0, если оба значения равны 1 (последняя строчка в таблице истинности). То есть ее результат — истина в том и только в том случае, когда два значения не равны. “Исключающее ИЛИ” в алгебре логики обозначается знаком “ ⊕ ”, в языке Паскаль как xor (например, “ A xor B ”), а в языке Си — знаком “ ^ ” (“ A ^ B ”). Эту операцию можно представить через базовые операции (“НЕ”, “И”, “ИЛИ”) следующим образом:
Импликация Мы часто используем логическую связку “если …, то”, например: “Если пойдет дождь, то я надену плащ” или “Если все стороны прямоугольника равны, то это квадрат”. В логике эта связка называется импликацией (следованием) и обозначается стрелкой: A→B (“если A, то B”, “из A следует B”). Импликацию можно заменить на выражение, использующее только базовые операции (здесь — только “НЕ” и “ИЛИ”):
Эквивалентность Эквивалентность (также эквиваленция, равносильность) — это логическая операция, которая соответствует связке “тогда и только тогда”. Высказывание A↔B истинно в том и только в том случае, когда A = B (см. таблицу истинности). Возможно, вы заметили, что эквивалентность — это обратная операция для “исключающего ИЛИ” (проверьте по таблицам истинности), то есть
Здесь черта сверху, охватывающая все выражение в правой части равенства, означает отрицание (инверсию), которое применяется к результату вычисления выражения A⊕B, а не к отдельным высказываниям. Можно заменить эквивалентность выражением, которое включает только базовые логические операции:
Другие логические операции
Мы уже говорили, что существуют и другие логические операции. Таблицы истинности операций с двумя переменными содержат 4 строки и отличаются только значением последнего столбца. Поэтому любая новая комбинация нулей и единиц в этом столбце дает новую логическую операцию (логическую функцию). Всего их, очевидно, столько, сколько существует четырехразрядных двоичных чисел, то есть 16 = 24. Из тех, что мы еще не рассматривали, наиболее интересны две — штрих Шеффера (“И–НЕ”, англ. nand = “ not and ”)
и стрелка Пирса (“ИЛИ–НЕ”, англ. nor = “ not or ”).
Штрих Шеффера
Стрелка Пирса
Логические выражения Обозначив простые высказывания буквами (переменными) и используя логические операции, можно записать любое высказывание в виде логического выражения. Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трех двигателей самолета. Обозначим высказывания: А — “Первый двигатель вышел из строя”. B — “Второй двигатель вышел из строя”. C — “Третий двигатель вышел из строя”. X — “Аварийная ситуация”. Тогда логическое высказывание X можно записать в виде формулы X =(A·B) + (A·C) + (B·C) (1). Таким образом, мы выполнили формализацию. Формализация — это переход от конкретного содержания к формальной записи с помощью некоторого языка. В логических выражениях операции выполняются в следующем порядке: 1) действия в скобках; 2) отрицание (“НЕ”); 3) логическое умножение (“И”); 4) логическое сложение (“ИЛИ”) и “исключающее ИЛИ”; 5) импликация; 6) эквивалентность. Такой порядок означает, что все скобки в выражении (1) для X можно убрать. Здесь каждая операция выполняется с двумя значениями. Такие операции называются бинарными (от лат. bis — дважды), или двуместными. Операции, которые выполняются над одной величиной, называют унарными (от лат. uno — один), или одноместными. Пример унарной логической операции — это отрицание (операция “НЕ”). Любую формулу можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Сложные выражения удобно разбить на несколько более простых, сначала вычислить значения этих промежуточных величин, а затем — окончательный результат.
Рассмотрим формулу (1). Выражение в правой части зависит от трех переменных, поэтому существует 23 = 8 комбинаций их значений. По таблице истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание “сегодня безветрие, и дует сильный ветер” никогда не может быть истинным. Соответствующее логическое выражение Упражнение 2. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? а) б) в) г)
Упражнение 3. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? а) б) в) г)
Законы алгебры логики Для упрощения логических выражений используют законы алгебры логики. Они формулируются для базовых логических операций — “НЕ”, “И” и “ИЛИ” (табл. 1). Закон двойного отрицания означает, что операция “НЕ” обратима: если применить ее два раза, логическое значение не изменится. Закон исключения третьего основан на том, что любое логическое выражение либо истинно, либо ложно (“третьего не дано”). Поэтому если A = 1, то Таблица 1 Законы алгебры логики
Распределительный закон для “ИЛИ” — это обычное раскрытие скобок. А вот для операции “И” мы видим незнакомое выражение, в математике это равенство неверно. Доказательство можно начать с правой части, раскрыв скобки:
Дальше используем закон повторения (A · A = A) и заметим, что
Аналогично доказываем, что
Равенство доказано. Попутно мы доказали также и закон поглощения для операции “И” (для “ИЛИ” вы можете сделать это самостоятельно). Отметим, что из распределительного закона следует полезная формула:
Правила, позволяющие раскрывать отрицание сложных выражений, названы в честь шотландского математика и логика де Моргана. Доказать законы де Моргана можно с помощью таблиц истинности. Рассмотрим пример:
Здесь последовательно использованы закон де Моргана, распределительный закон, закон исключения третьего, переместительный закон, закон повторения, снова переместительный закон и закон поглощения. Упражнение 4. Упростите логические формулы: а) б) в) г) д) Упражнение 5. Определите с помощью таблиц истинности, какие из следующих формул являются тождественно истинными или тождественно ложными: а) б) в) Упражнение 6. Пусть а = ”это утро ясное”, а b = ”это утро тёплое”. Выразите формулы на обычном языке:
а) б) в) Упражнение 7. Постройте таблицы истинности для логических формул и упростите формулы, используя законы логики: а) б) в)
Синтез логических выражений До этого момента мы считали, что логическое выражение уже задано, и нам надо что—то с ним сделать (построить таблицу истинности, упростить и т.п.). Такие задачи называются задачами анализа (от греч. разложение) — мы исследуем имеющееся выражение. При проектировании различных логических устройств, в том числе и узлов компьютеров, приходится решать обратную задачу — строить логическое выражение по готовой таблице истинности, которая описывает нужное правило обработки данных. Эта задача называется задачей синтеза (от греч. совмещение). В качестве простейшего примера построим логическое выражение для операции импликации
Например, выражение Складывая выражения для всех отмеченных строк (кроме третьей, где функция равна нулю), получаем
Таким образом, мы вывели формулу, которая позволяет заменить импликацию через операции “НЕ” и “ИЛИ”.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.213.128 (0.069 с.) |
 или А, в языках программирования Паскаль и Бейсик — как not A, в языке Си — как !A.
или А, в языках программирования Паскаль и Бейсик — как not A, в языке Си — как !A.
 лампочки используются два выключателя, соединенных последовательно (см. рис.).
лампочки используются два выключателя, соединенных последовательно (см. рис.). Можно представить себе схему с двумя выключателями, соединенными параллельно (см. рис.). Чтобы лампочка загорелась, достаточно включить хотя бы один из выключателей. Чтобы выключить лампочку, необходимо обязательно выключить оба.
Можно представить себе схему с двумя выключателями, соединенными параллельно (см. рис.). Чтобы лампочка загорелась, достаточно включить хотя бы один из выключателей. Чтобы выключить лампочку, необходимо обязательно выключить оба.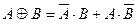 .
.





 всегда ложно, оно называется тождественно ложным, или противоречием. Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными, или тождественно равными.
всегда ложно, оно называется тождественно ложным, или противоречием. Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными, или тождественно равными. ;
; ;
; ;
; ;
;
 ;
; ;
; ;
; ;
;
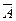 = 0 (и наоборот), так что произведение этих величин всегда равно нулю, а сумма — единице.
= 0 (и наоборот), так что произведение этих величин всегда равно нулю, а сумма — единице.


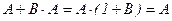 , таким образом,
, таким образом,


 ; е)
; е)  ;
;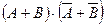 ; ж)
; ж)  ;
; ; з)
; з)  ;
; ; и)
; и)  .
. ;
; ;
; ;
;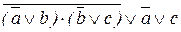 .
. ; г)
; г)  ; ж)
; ж)  ; к)
; к)  ;
; ; д)
; д)  ; з)
; з)  ; л)
; л)  .
. ; е)
; е)  ; и)
; и)  ;
; ;
; ;
; .
. . В таблице истинности мы выделяем все строки, где логическое выражение равно единице. Тогда выражение может быть записано как логическая сумма выражений, каждое из которых истинно только в одном случае.
. В таблице истинности мы выделяем все строки, где логическое выражение равно единице. Тогда выражение может быть записано как логическая сумма выражений, каждое из которых истинно только в одном случае.
 истинно только при А= 0 и B = 0, то есть только в первой строке таблицы. Выражение
истинно только при А= 0 и B = 0, то есть только в первой строке таблицы. Выражение  истинно только во второй строке, а
истинно только во второй строке, а  — только в последней. Существует простое правило: если в этой строке переменная равна нулю, она входит в произведение с отрицанием, а если равна 1, то без отрицания.
— только в последней. Существует простое правило: если в этой строке переменная равна нулю, она входит в произведение с отрицанием, а если равна 1, то без отрицания. . Упрощаем выражение:
. Упрощаем выражение: .
.


