
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества и операции над ними. Множества действительных чисел, числовые промежутки. Окрестность и проколотая окрестность точки.Стр 1 из 6Следующая ⇒
Основные элементарные функции и их графики 1) Показательная функция y=ax, a>0, a≠1. 2) Степенная функция y=xα, 3) Логарифмическая функция 4) Тригонометрические функции y=sinx, y=cosx, y=tgx, y=ctgx 5) Обратные тригонометрические функции y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. Функция, задаваемая одной формулой, составленной из основнх элементарных функций и постоянных с помощью конечного числа арифметических операций и операций взятия функции от функции, называется элементарной функцией.
Числовые последовательности. Определение монотонной и ограниченной последовательности. Предел последовательности. Основные теоремы о пределах. · Под числовой последовательностью Х1,X2…… понимается функция Хn=f(n) заданная на множестве N натуральных чисел. · Обозначение: хn, n ϵ N. Число х1 называется первым членом последовательности, х2 вторым…. Хп – общим членом последовательности. · Последовательность называется ограниченной если существует такое число М>0, что для любого n ϵ N выполняется неравенство Xn ≤ M · Последовательность называется возрастающей если для любого n выполняется неравенство an+1>an. Для убывающей последовательности наоборот. · Все эти последовательности называются монотонной последовательностями. · Число а называется пределом числовой последовательности {хn} если для любого положительного числа ɛ найдется такое натуральное число N что при всех n>N выполняется неравенство |xn-a|<ɛ · Последовательность, имеющая конечный предел называется сходящейся, а не имеющая пределов - расходящейся. Основные теоремы о пределах · Если · Если · Теорема Вейерштрасса.
Признаки существования пределов. Первый и второй замечательные пределы. Теорема 1. О пределе промежуточной функции. Если функция f(x) заключена между двумя функциями φ(x) и g(х), стремящимися в одному и тому же пределу, то она также стремится к этому пределу, т.е. если Теорема 2. О пределе монотонной функции. Если функция f(x) монотонна и ограничена при х>х0 или при х<х0, то существует соответственно ее левый предел
Следствие: Ограниченная монотонная последовательность xn, Первый замечательный предел: Предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю:
Второй замечательный предел:
Замечания: Сравнение бесконечно малых функций и теоремы о них. Таблица эквивалентных бесконечно малых функций. Сравнение бмф. Пусть Данные бмф можно сравнить с помощью отношений: 1) 2) 3) 4) Замечания: х→+∞, х→х0-0, х→х0+0 Теоремы о бмф. Теорема1. Предел отношения двух бмф не изменится если каждую из нх заменить эквивалентной. Пример: Теорема 2. Разность двух эквивалентных бмф, есть бмф более высокого порядка, чем каждая из них. Пример: Теорема 3. Сумма конечного числа бмф разного порядка эквивалентна слагаемому низшего порядка, чем остальные, при х→х0 Эквивалентные функции. Опр.1. Пусть Таблица эквивалентных бмф при х→0 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Производная сложной и обратной функций. Таблица производных элементарных функций. Теорема 1. Пусть функция y=f(x) имеет производную в (.)х0, т.е. Замечание: теорема дифференцирования сложной функции распространяется на конечное число вложений функции. Z(t)=z(φ(y(t))), при этом существует z′φ, φ′y, y′t, то z′(t)= z′φ∙φ′y∙ y′t Теорема 2. Пусть y=f(x) строго монотонна на (a,b). Иначе: Производная обратной функции равна обратной величине производной данной функции.
Таблица производных:
14. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование, пример. Пусть y=f(x) на [a,b], то говорят, что функция задана явно. Однако функция может быть задана неявно и параметрически. Опр.1. Функция задана неявно на интервале (a,b), если она определяется уравнением f(x,y)=0 (1), не разрешенным относительно y. Замечания: Правило1. Нахождение y′(x) для функции, заданной неявно уравнение (1): 1) Дифференцируем уравнение(1) по переменной х, рассматривая при этом y как функцию y(x). 2) Из полученного уравнения выражаем y′(x) Опр.2. y=f(x) задана параметрически, если независимая переменная х и зависимая переменная y связаны между собой параметрической системой уравнений: x=x(t); y=y(t); 1) Пусть 2) X(t) имеет обратную функцию t(x) Правило 2. Дифференцирование параметрически заданной функции с помощью (2) 1) Вычислить производные x′(t), y′(t) 2) По правилу дифференцирования сложной функции y=y(t)=y(t(x)) имеем y′(x)=y′(t)∙t′(x) 3) По правилу дифференцирования обратной функции из полученного равенства имеем: Иногда при нахождении производных от сложных функций применяют логарифмическое дифференцирование. Правило 3. 1) Исходную функцию логарифмируют 2) Полученную логарифмическую функцию дифференцируют и выражают y′(x) Правило 3 применяют для степенно-показательных функций. Утверждение: y=U(x)V(x) Справедлива формула дифференцирования:
Первообразная. Неопределенный интеграл, его основные свойства. Таблица основных интегралов. Опр.1. Функция F(x) называется первообразной функции f(x) на интервале (a;b), если для любого x Опр.2. Совокупность всех первообразных φ(x) x Таким образом, по определению Здесь f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования, ∫- знаком неопределенного интеграла. Теорема о существовании неопределенного интеграла: если функция y=f(x) непрерывна на (a;b), то для f(x) существует первообразная, а тогда существует и неопределенный интеграл. Пусть F(x) – первообразная функции f(x), где Док-во: рассм. правую часть (2) (F(x)+C)′= F′(x)+C′=f(x)⇒ F(x)+C – первообразная функции f(x) Пусть φ(x) – другая первообразная функции f(x), причем T(x)≠F(x), тогда t′(x)=f(x) для Сво-ва неопредел. Интеграла. 1) Дифференциал от интеграла d(S(f(x)dx)=d(F(x)+C=dF(x)+dC Док-во: (S(f(x)dx)=d(F(x)+C=dF(x)+dC=dF(x)=F′(x)dx Следствия (f(x)dx)′=f(x)dx 2) 3) 4) Инвариантность форм интегрирования Пусть F(x) – первообразная f(x)
Таблица интегралов:
21. Непосредственное интегрирование, подведение заданного выражения под знак дифференциала, примеры. Замена переменной в интеграле, подстановка. Интегрирование по частям, типы интегралов, для которых применяется интегрирование по частям.
П.1 метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. При сведение данного интеграла к табличному часто используются следующие преобразования дифференциала («подведение под знак дифференциала»):
Замена переменной в интеграле Метод интегрирования подстановкой заключается в введении переменной интегрирования. При этом интеграл приводится к новому интегралу, который является табличным или к нему сводится. Пусть требуется вычислить интеграл Метод интегрирования по частям Пусть u=u(x) и V=V(x) – функции, имеющие непрерывные производные. Тогда d(uv)=u∙dv + v∙du. Интегрируя это равенство, Полученная формула называется формулой интегрирования по частям. Она позволяет свести вычисление интеграла Типы интегралов, для которых удобен метод интегрирования по частям. 1) Интегралы вида 2) Интегралы вида 3) Интегралы вида 22. Дробно – рациональная функция (рациональная дробь). Четыре типа простейших дробей. Теорема о разложении рациональной дроби. Метод неопределенных коэффициентов, пример. Опр.1. Дробно – рациональной функцией или рациональной дробью называется отношение многочленов: Утв. Неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби. Например: 4 типа простейших рациональных дробей 1) 2) 3) 4) Теорема 1. Разложение правильно1 рациональной дроби на сумму простейших дробей: Пусть прав. рацион. дробь
Для нахождения неопределенных коэффициентов используется метод уравнения левой и правой части. Идея метода сравнения: 1) В правой части равенства (2) приводим к общему знаменателю 2) Т.е. в полученном равенстве равны знаменатели, а числители равны: Pn(x)=S(x) 3) Сравниваем коэф. при одинаковых степенях x, получим систему алгебраических линейных уравнений, относительно коэф. A,A1…B,B1. Замечания: при нахождении неорп. коэф. в третьем пункте используют иногда смешанный прием, т.е. пусть x=x1; x=x2, из которых определяют неопр. коэф., если остаются неопр.коэф. применяют метод сравнения. Множества и операции над ними. Множества действительных чисел, числовые промежутки. Окрестность и проколотая окрестность точки. Множества и операции над ними · Множество – совокупность некоторых объектов, объединенных по какому либо признаку. · Объекты, из которых состоит множество, называются его элементами. Мн-ва обозначаются заглавными буквами: A,B,C,D…, а элементы: a,b,c,d… · Если элемент принадлежит множеству, то записывают х∈ Х. · Если элемент не принадлежит, то записывают х∉ Х. · Множество, не содержащее ни одного элемента, называют пустым и обозначают ∅ · Элементы множества записываются в фигурных скобках: А={1,2,3,4}, если же множество записано как А={х: 0 ≤ х ≤ 2}, то означает, что множество А состоит из всех действительных чисел, удовлетворяющих 0 ≤ х ≤ 2 Действия над множествами · Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В: А ⊂ В. · Если А ⊂ В и В ⊂ А, значит множества равны или совпадают: А=В. Множества, состоящие из одних и тех же элементов, называются равными. · Объединением (суммой) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств: А ∪ В. · Пересечением (произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит и А, и В: А∩ В. Множества действительных чисел Множества, элементами которых являются числа, называются числовыми. N = {1;2;3;…;n;…} – множество натуральных чисел Z0 = {0;1;2;…;n;…} – множество целых неотрицательых числе Z = {0;±1;±2;…;±n;…} – множество целых числе Q = { R – множество действительных чисел. Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической: Действительные числа, не являющиеся рациональными, называются иррациональными. Множество R действительных чисел обладает следующими свойствами: А) оно упорядоченное: для двух любых различных чисел a и b имеет место одно из двух соотношений: a < b либо b < a Б) множество R плотное: между любыми двумя различными числами a и b содержится бесконечное множество действительных чисел х, т.е. чисел удовлетворяющих неравенству a<x<b
В) множество R непрерывное. Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных числе и множеством всех точек прямой. Это означает, что каждому числу х∈ R соответствует определенная единственная точка на числовой оси и, наоборот, каждой точке оси соответствует определенное действительное число. Числовые промежутки, окрестность и проколотая окрестность точки Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид: [a;b] = {x: a≤x≤b} - отрезок (сегмент, замкнутый промежуток) (a;b) = {x: a<x<b} - интервал (открытый промежуток) [a;b) = {x: a≤x<b} - полуоткрытые интервалы (полуоткрытые отрезки) (a;b] = {x: a<x≤b} (-∞;b] = {x: x≤b}; (-∞;b] = {x: x<b} [a;+∞) = {x: x>a}; [a;+∞) = {x: x≥a} (-∞;∞) = {x: -∞<x<+∞} - бесконечные интервалы (промежутки) Окрестностью точки х0 называется любой интервал (a,b), содержащий точку х0. В частности, интервал (х0-ɛ, х0+ɛ), где ɛ>0, называется ɛ-окрестностью точки х0. Число х0 называется центром, а ɛ– радиусом. 2. Функция, ее способы задания. Классификация функций – ее основные характеристики. Соответствия f, которое каждому элементу х∈Х сопоставляет один и только один элемент y∈Y, называется функцией и записывается y=f(x),х∈Х. Говорят, что функция f отображает множество Х на множество Y. Если элементами множеств X и Y являются действительные числа(R), то функцию называют числовой функцией. Графиком функции y=f(x) называется множество всех точек плоскости Oxy, для каждой из которых х является значением аргумента, а у - соответствующим значением функции. Способы задания функций. а) Аналитический способ: функция задается в виде одной или нескольких формул или уравнений. Этот способ является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию y=f(x). б) Графический способ: функция задается графиком. Преимуществом графического способа является наглядность, недостатком – неточность. в) Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. На практике часто приходится пользоваться таблицами значений, полученных опытным путем или в результате наблюдений. Основные характеристики функций 1) Функция y=f(x), определенная на множестве D, называется четной, если каждый х ∈ D выполняются условия –х ∈ D и f(-x)=f(x); нечетной, если каждый х ∈ D выполняются условия –х ∈ D и f(-x)=-f(x). 2) Если для любых значений х1,х2 ∈ D1 аргументов из неравенства х1<х2 вытекает неравенство: f(x1)<f(x2), то функция называется возрастающей; f(x1)≤f(x2) – неубывающей; f(x1)>f(x2) – убывающей; f(x1)≥f(x2) – невозрастающей на множестве D1. Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D1 называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. 3) Функцию y=f(x), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М>0, что для всех х∈D выполняется неравенство |f(x)|≤М. отсюда следует, что график ограниченной функции лежит между прямыми y=-М и y=М. 4) Функция y=f(x), определенная на множестве D, называется переодической на этом множестве, если существует такое число Т>0, что при каждом х
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.240.178 (0.111 с.) |
 R
R , a>0, a≠1
, a>0, a≠1 и начиная с некоторого номера n, выполняется неравенство xn ≤ yn,a ≤ b
и начиная с некоторого номера n, выполняется неравенство xn ≤ yn,a ≤ b и справедливо неравенство хп ≤zn≤yn, начиная с некоторого n. Тогда
и справедливо неравенство хп ≤zn≤yn, начиная с некоторого n. Тогда  .
. монотонная ограниченная последовательность имеет предел.
монотонная ограниченная последовательность имеет предел.

 или ее правый предел
или ее правый предел 
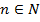 , имеет предел.
, имеет предел.


 бмф, при х→х0, т.е.
бмф, при х→х0, т.е.  ,
, 
 M≠0, тогда α,β-бмф одного порядка
M≠0, тогда α,β-бмф одного порядка
 , тогда α и β – не сравнимые бмф при х→х0
, тогда α и β – не сравнимые бмф при х→х0
 . Справедливо и обратное.
. Справедливо и обратное. , то α и β называются эквивалентными бмф, при х→х0. Обозн.
, то α и β называются эквивалентными бмф, при х→х0. Обозн.  , при х→х0
, при х→х0








 , в частности
, в частности 
 f′(x0), z=g(y) имеет производную в (.) y0, где y0=f(x0) (
f′(x0), z=g(y) имеет производную в (.) y0, где y0=f(x0) ( обратная функция x=φ(y) имеет производную φ′(y), при этом справедлива формула φ′(y)=
обратная функция x=φ(y) имеет производную φ′(y), при этом справедлива формула φ′(y)= 
 ; следствие:
; следствие:  5)
5) 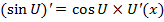 6)
6)  7)
7)  8)
8) 
 10)
10)  11)
11)  12)
12)  13)
13) 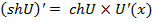 ;
;  14)
14) 
 15)
15)  ;
;  16)
16)  ;
; 
 (2)
(2) t для всех
t для всех  (3)
(3)
 (a;b) выполняется равенство F′(x)=f(x) (1)
(a;b) выполняется равенство F′(x)=f(x) (1)
 ; тогда
; тогда  (2)
(2)
 - линейность
- линейность ; U=T(x) -
; U=T(x) -  , где F(u) – первообразная функции f(u)
, где F(u) – первообразная функции f(u) 2)
2)  3)
3) 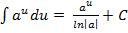 4)
4)  5)
5) 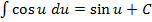 6)
6)  7)
7)  8)
8)  9)
9) 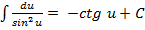
 11)
11)  12)
12)  13)
13)  14)
14) 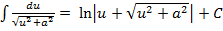 15)
15) 

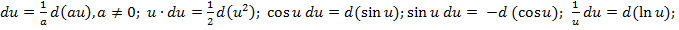

 . Сделаем подстановку x=φ(t), где φ(t) – функция, имеющая непрерывную производную. Тогда dx=φ′(t)dt на основании св-ва инвариантности формулы интегрирования неопр. интеграла получаем формулу интегрирования подстановкой:
. Сделаем подстановку x=φ(t), где φ(t) – функция, имеющая непрерывную производную. Тогда dx=φ′(t)dt на основании св-ва инвариантности формулы интегрирования неопр. интеграла получаем формулу интегрирования подстановкой: 

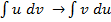 , который является более простым или табличным.
, который является более простым или табличным. ,
, 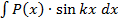 ,
,  – многочлен, k – число. Удобно u=P(x), dv – все остальное
– многочлен, k – число. Удобно u=P(x), dv – все остальное ,
, 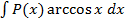 ,
, 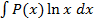 ,
,  ,
,  . Удобно: P(x)dx=du, а за u обозначить остальные сомножители.
. Удобно: P(x)dx=du, а за u обозначить остальные сомножители. ,
,  , где a и b – числа. За u можно принять функцию u=eax.
, где a и b – числа. За u можно принять функцию u=eax.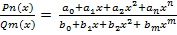 (1), если n
(1), если n  m, то дробно – рациональная функция неправильная, если n<m, nj (1) – правильная
m, то дробно – рациональная функция неправильная, если n<m, nj (1) – правильная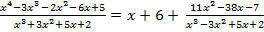
 ; A,a – const
; A,a – const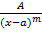 ; m≥2, m
; m≥2, m 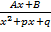 ; A,B,p,q – const, D=p2-4q<0
; A,B,p,q – const, D=p2-4q<0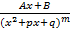 ; m≥2; D<0
; m≥2; D<0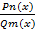 , n<m, Qn(x)=(x-x1)(x-x1)2…(x-x1)k1(x-x2)…(x-x2)k2…(x2+px+q)…(x2+p0x+qu)qu , где действ. корни: х1, х2… имеют кратность соответственно k1,k2. тогда рацион. дробь представляется в виде суммы простейших дробей.
, n<m, Qn(x)=(x-x1)(x-x1)2…(x-x1)k1(x-x2)…(x-x2)k2…(x2+px+q)…(x2+p0x+qu)qu , где действ. корни: х1, х2… имеют кратность соответственно k1,k2. тогда рацион. дробь представляется в виде суммы простейших дробей. (2)
(2) - неопределенные коэффициенты
- неопределенные коэффициенты , где S(x) – многочлен в неопр. коэф.
, где S(x) – многочлен в неопр. коэф. ; m ∈ Z, n ∈ Z} – множество рациональных чисел
; m ∈ Z, n ∈ Z} – множество рациональных чисел =0,5(=0,500…),
=0,5(=0,500…),  - рациональные числа.
- рациональные числа. , где m=±1,±2,… так для y=sinx периодами будут числа ±2
, где m=±1,±2,… так для y=sinx периодами будут числа ±2  ,±4,±6π,… обычно за период берут наименьшее положительное число Т, удовлетворяющее равенству f(x+T)=f(x).
,±4,±6π,… обычно за период берут наименьшее положительное число Т, удовлетворяющее равенству f(x+T)=f(x).


