
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство аддитивности также говорит О том, что сигналы проходящие через линейную систему не оказывают влияния друг на друга. Наличие любой нелинейности нарушает это утверждение.
Факт линейности или нелинейности того или иного элемента, системы может быть установлен либо экспериментально либо по уравнениям описывающим поведение системы. Если все элементы, входящие в систему, линейны, то и система будет линейной. Если хотя бы один элемент системы представляет собой нелинейный элемент, то и вся система будет нелинейной. Линейное дифференциальное уравнение n- го порядка, связывающее выход х со входом у в общем случае имеет вид:
Нелинейное дифференциальное уравнение, связывающее выход со входом
Нелинейные члены – любая, не равная 1 (α≠1) степень переменной хα., либо произведение управляемых, либо управляющих координат х, у, либо управляемая координата – аргумент нелинейной функции. Все это делает уравнение нелинейным. Также, нелинейными являются уравнения.
Приведем ещё один пример нелинейных систем. Этому примеру соответствует электродвигатель, скорость вращения вала которого пропорциональна до определенных пределов входному управляющему сигналу. Однако, при больших входных сигналах электродвигатель либо сгорит, либо разрушится и поэтому входной сигнал надо ограничивать чему соответствует и ограничение скорости электродвигателя.
В этой системе имеется нелинейность F типа «насыщения». Если на нелинейности F входной сигнал 1, то выходной – 5. Если входной сигнал 2, то выходной – 10. Если входной сигнал 3, то выходной сигнал по прежнему 10. Таким образом в нелинейных системах нарушается пропорциональность между входом и выходом. Принцип суперпозиции при e(t)>2 не выполняется. При входном сигнале 1+2=3, выходной сигнал будет не 5+10=15 – что было бы, если бы система была линейной, а выходной сигнал будет по прежнему 10. Аппарат исследования линейных систем разработан и достиг относительного совершенства. Аппарат исследования нелинейных систем только еще разрабатывается. Хотя численное решение системы нелинейных уравнений в том числе и дифференциальных всегда возможно на компьютере, но эти решения не обладают достаточной общностью.
Линеаризация уравнения колебаний физического маятника.
Из за относительной простоты получения решения всегда существовала и сейчас существует тенденция свести нелинейное уравнение к линейному операцией, так называемой, линеаризации. Это часто возможно сделать, если принять какое-то опорное состояние и записать уравнения системы в малых отклонениях – вариациях от этого опорного состояния. В предположении малости этих вариаций, поддерживаемых системой, можно получить линеаризованное уравнение системы. Рассмотрим колебания физического маятника.
L
Это нелинейное уравнение относительно рассматриваемой координаты θ, которая является аргументом нелинейной функции sin. Однако, разложим функцию sin(θ) в степенной ряд.
При малых θ – члены θ3 и θ5 гораздо меньше, чем θ и ими можно пренебречь. При Итак уравнение колебаний маятника
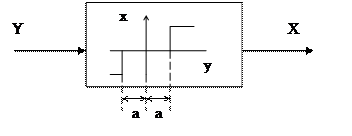
Нелинейные модели исполнительных органов автоматических и автоматизированных систем математическое моделирование нелинейных систем Существуют виды ИО, которые создают существенно нелинейные воздействия на ОУ. Это например электродвигатели не имеющие пропорционального управления по скорости вращения вала, а имеющие постоянную скорость, изменяемую скачком от нуля при подаче сигнала включить.
Связь между Х и Y не линейна, с зоной нечувствительности.
Такой же характеристикой обладают микроракетные двигатели системы ориентации космических аппаратов, электропривод постоянной скорости. Управление ими сводится к выдаче сигналов вкл.,выкл с учетом операции выбора знака. Если выключение такого релейного исполнительного органа производить при достижением ОУ заданного значения управляемой координаты,например, 0, то поскольку в этот момент скорость ОУ не равна 0, он проскочит заданное положение и начнется увеличение управляемой координаты, но с обратным знаком. Это приведет к включению релейного управления для его парирования также с обратным знаком. Релейный управляющий орган будет включен до тех пор пока управляемая координата не станет равной 0, но благодаря наличию скорости в этот момент ОУ опять проскочит заданное положение и т.п.
В таких нелинейных системах ОУ и управляемые координаты находятся в автоколебательном режиме – режиме незатухающих колебаний с более или менее постоянной амплитудой. Общих методов анализа и синтеза нелинейных систем не существует. Имеются методы для анализа отдельных видов нелинейных систем, например, релейных, но ни один из них не является универсальным. Учитывая сказанное, в анализе и синтезе нелинейных систем определяющее значение приобретает имитационное математическое моделирование их работы. Рассмотренные нелинейности исполнительных органов легко описываются и программируются при помощи ряда логических условий. Вопросы для повторения Математические модели для исследования поведения системы. Адекватность математических моделей. Непрерывные и дискретные во времени математические модели, математические модели, основанные на дискретных событиях Математические модели объектов управления мехатронных систем Линейные системы, нелинейные системы, их линеаризация. Линеаризация уравнения колебаний физического маятника. Нелинейные модели исполнительных органов автоматических и автоматизированных систем Запаздывания и упреждения при управлении ТС. Лекция 3. Качество процессов управления и методы его исследования. Устойчивость систем управления. Корни характеристического уравнения. Преобразование Лапласа Качество процессов управления. Методы анализа качества процессов управления
Рассмотрение решения линейных, а затем нелинейных дифференциальных уравнений, описывающих СУ не самоцель. Это средство исследования поведения динамических систем, которые моделируются (описываются) этими уравнениями. Что волнует пользователей и стало быть разработчиков автоматических и автоматизированных систем управления, какие характеристики процессов управления важны для них? 1.Во всех случаях мы требуем, чтобы система управления предсказуемым образом реагировала на входные воздействия и начальные условия. Для этого система должна быть устойчивой Т.е. её отклонения от заданного состояния должны быть ограничены. Если это не так, то система не может использоваться практически - неработоспособна. 2.Поскольку никогда нельзя получить точную модель физической системы, то полученные при проектировании характеристики математической модели системы должны быть малочувствительными к малым изменениям параметров модели системы т.е. должна иметь место параметрическая устойчивость системы и её математической модели (грубость системы). Следовательно чувствительность системы к изменению её параметров всегда представляет практический интерес. 3. Все реальные системы подвержены внешним воздействиям – возмущениям. Система должна им противостоять. Поэтому важную роль приобретает способность системы подавлять возмущения. В том числе и случайные, и плохо определенные. Обратная связь с этим неплохо справляется. 4. Для большинства систем важна точность работы, которая оценивается максимальным, средне интегральным или установившимся отклонением фазовых управляемых координат системы от заданных значений. 5.Для некоторых систем терминального управления основной характеристикой является время перехода из первоначального состояния в заданное конечное.
Теория управления – обширная наука, которая базируется на исследовании математических моделей, причем исторически так сложилось, что далеко не всегда это исследование производилось прямым решением систем уравнений, их описывающих, так как в докомпьютерную эру это представляло определенную трудность. Было изобретено множество методов оценки качества процессов управления и устойчивости по анализу коэффициентов уравнений, частотные методы, которые до сих пор изучаются в более полных курсах теории управления. Появление и распространение цифровых вычислительных машин (ЦВМ) позволило перейти от косвенных и приближенных методов исследования к прямому численному решению (интегрированию) уравнений моделей систем, что в ряде случаев проще и быстрее. Однако, эти методы дают частные решения т.е. не обладают необходимой общностью. Поэтому классические методы исследования устойчивости, например, сохранили свое значение для моделей невысокого порядка, для которых возможно получение аналитических решений. Мы также избираем в нашем курсе кратчайший путь для объяснения важнейших особенностей цифровых систем управления СТС и определения качества процессов управления, путем численного математического моделирования, пользуясь доступностью в настоящее время методов численного интегрирования на ЦВМ системы дифференциальных уравнений, описывающих поведение системы. Базовый и простейший из них – метод Эйлера будет нами рассмотрен.
Устойчивость систем управления. При анализе и синтезе реальных систем управления с отрицательной обратной связью первостепенное значение имеет анализ устойчивости. Устойчивая система – это динамическая система, обладающая ограниченной реакцией на ограниченный входное воздействие. сигнал. В неустойчивых системах отклонения управляемых координат от требуемых значений могут увеличиваться с течением времени неограниченно Считается, что с практической точки зрения неустойчивая система не имеет смысла. Это не совсем так для системы с переменными по времени коэффициентами, когда кратковременная неустойчивость быстро проходит и система опять становится устойчивой, не успев «разболтаться», но тем не менее в общем случае неустойчивая система практического значения не имеет.
Многие реальные объекты неустойчивы в разомкнутом состоянии (без замыкания обратной связи системы управления). При этом они имеют не только большие ошибки при работе, а просто не могут функционировать (ракеты, некоторые самолеты). Для них автоматическая система управления обязательна. Правильным выбором управления неустойчивая система может быть сделана устойчивой.
Имеются более строгие определения. Однако, для целей нашего анализа этих определений достаточно.
Характеристическое уравнение и его корни.
Рассмотрим линейное однородное (правая часть равна 0) дифференциальное уравнение порядка n с постоянными коэффициентами, описывающее поведение системы.
Вид уравнения показывает, что решение этого уравнения следует искать прежде всего среди функций, которые алгебраически подобны своим производным. Этим свойством обладает показательная функция, поэтому будем искать решение в виде:
Так как
…
подставив значения этих производных в исходное уравнение, имеем:
Так как
Это – алгебраическое уравнение степени n.Оно имеет n корней. Корни этого характеристического уравнения r1…rn позволяют записать общее решение исходного дифференциального уравнения в виде:
Здесь c1, c2, c3, …, cn - постоянные, определяемые из начальных условий, r1 ... rn - корни характеристического уравнения n-ой степени. Решение этого линейного дифференциального уравнения общего вида будет устойчивым (ограниченным) при
Значение мнимой части корня ( Таким образом, для определения характера поведения линейной системы важным является найти характеристическое уравнение и определить его корни или, по крайней мере, определить знак действительной части корней. Это сразу позволит сказать «правильная» ли это система уравнений и правильны ли значения ее параметров. Годится ли все это для практического использования.
Методы анализа устойчивости систем управления.
При анализе и синтезе реальных систем управления с обратной связью первостепенное значение имеет анализ устойчивости. Сначала кратко рассмотрим устойчивость непрерывных линейных систем Рассмотрим плоскость S – плоскость корней характеристического уравнения. Необходимое и достаточное условие устойчивости замкнутой системы: все корни характеристического уравнения замкнутой системы имеют отрицательную действительную часть. Поэтому чтобы провести анализ устойчивости системы управления необходимо найти корни её характеристического уравнения.
Аналитически корни характеристического уравнения могут быть определены в общем случае для уравнения не выше третьей степени (в частных случаях выше). Приближенные численные методы для нахождения корней характеристического уравнения поэтому были изобретены давно. Но пока не было компьютеров при исполнении этой большой вычислительной работы возникали понятные трудности. Поэтому в докомпьютерную эпоху инженеры изобрели несколько способов определения знаков действительных частей корней характеристического уравнения без нахождения непосредственно корней, используя: 1.Анализ коэффициентов и групп коэффициентов характеристического уравнения (критерий Рауса - Гурвица) 2.Графоаналитические методы анализа в частотной области, позволяющие использовать и экспериментально полученные частотные характеристики отдельных звеньев системы в общем расчете ее устойчивости. В настоящее время вычисление корней численными методами на ЦВМ не представляет особых трудностей. Объем курса не позволяет подробно останавливаться на этих методах. К тому же более универсальным с учетом возможных нелинейностей математических моделей, переменности по времени их коэффициентов будет метод прямого решения уравнений математических моделей путем численного их интегрирования. Тем не менее, учитывая, что для рассматриваемых нами СТС удовлетворительное по точности описание поведения систем приводит к уравнению не выше третьего порядка(инерционный объект управления + инерционный регулятор ). Поэтому запишем критерий Гурвица для характеристического уравнения третьей степени. a0s3+ a1s2 + a2s + a3 = 0
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.232 (0.036 с.) |
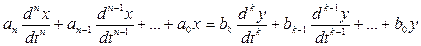
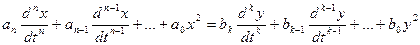
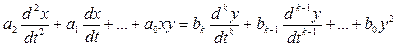
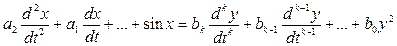
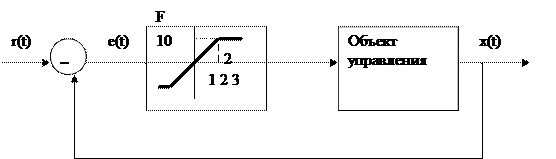

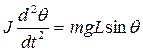
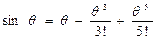 +…..
+…..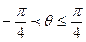 с ошибкой меньше чем 2% можно считать sin(θ)= θ.
с ошибкой меньше чем 2% можно считать sin(θ)= θ.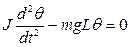 - это линейное (линеаризованное) уравнение, справедливое для
- это линейное (линеаризованное) уравнение, справедливое для 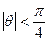 .
.
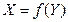
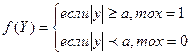
 Другое определение. Устойчивая система при отклонении от положения равновесия возвращается в равновесное положение за ограниченное время.
Другое определение. Устойчивая система при отклонении от положения равновесия возвращается в равновесное положение за ограниченное время.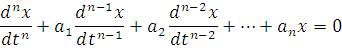
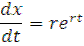
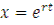
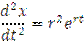
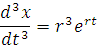
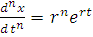 , то
, то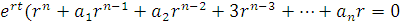
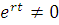 всегда, то имеем алгебраическое уравнение для исходного дифференциального уравнения, называемое характеристическим уравнением
всегда, то имеем алгебраическое уравнение для исходного дифференциального уравнения, называемое характеристическим уравнением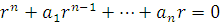
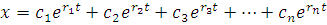
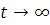 , если корни характеристического уравнения будут иметь отрицательную действительную часть, так как в общем случае корни характеристического
, если корни характеристического уравнения будут иметь отрицательную действительную часть, так как в общем случае корни характеристического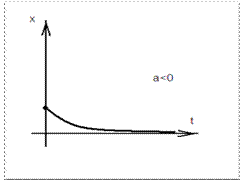
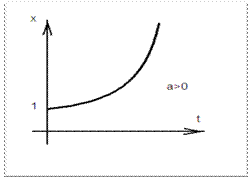 уравнения могут быть комплексными числами
уравнения могут быть комплексными числами 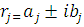 .
.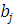 ) определяет частоты гармонических составляющих решения.
) определяет частоты гармонических составляющих решения.


