
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
А. М. Лихтер, О. Н. Гречухина, А. А. ПоповСтр 1 из 32Следующая ⇒
КИНЕМАТИКА
1. 1. Кинематика поступательного движения
Наиболее простым примером механического движения является движение материальной точки. Материальная точка –это тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки – абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки. Для определения положения тела в пространстве нужно использовать систему отсчета. Существует (наиболее употребительные) два способа описания движения тела (точки): векторный способ и координатный. Рассмотрим движение материальной точки в прямоугольной декартовой системе координат, поместив начало координаты в некую неподвижную точку О.
Уравнение пути: S = f(t) S≥0. (2) В зависимости от формы траектории движения: а) прямолинейное _______ б) криволинейное ~~~~, O (частный случай – вращательное движение) Вместо трех уравнений для координат движущейся точки ее движение можно задать одним векторным уравнением:
где Вектор Опыт 1.1. Равномерное движение Цель работы: наблюдение зависимости координаты, скорости и ускорения от времени при равномерном движении. Оборудование: 1. Дорожка с воздушной подушкой. 2. Компрессор. 3. Оптические датчики. 4. Тележка. 5. Компьютер.
Рис. 2. Демонстрация опыта
Ход работы На дорожке, установленной горизонтально, можно наблюдать практически равномерное движение тележки, после толчка, который создается электромагнитной пушкой.
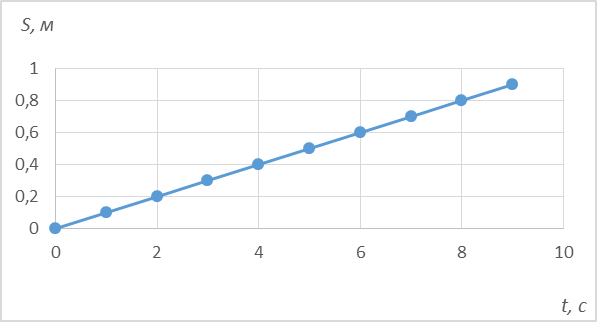
1. На экране дисплея наблюдаем линейную зависимость координаты от времени при равномерном движении тележки по горизонтальной дорожке.
Рис. 3. Зависимость координаты от времени
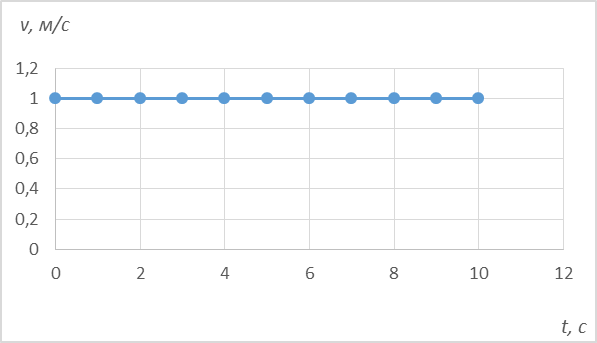
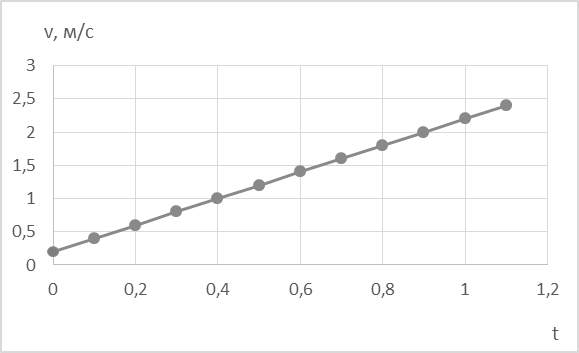
2. Скорость от времени практически не зависит (прямая линия).
Рис. 4. Зависимость скорости от времени
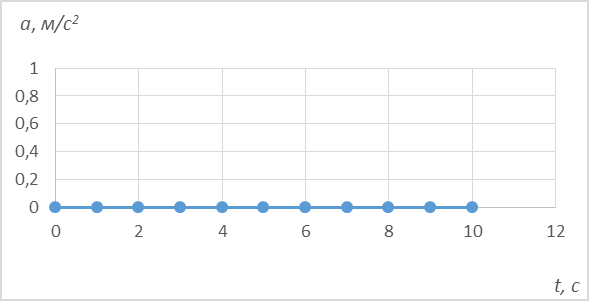
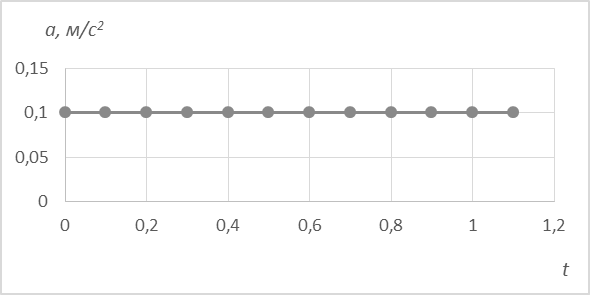
3. Видно, что ускорение при равномерном движении близко к нулю.
Рис. 5. Зависимость ускорения от времени
Вывод: продемонстрированы зависимости координаты, скорости и ускорения от времени при равномерном движении.
Ход работы 1. Дорожка на воздушной подушке снабжена большим количеством больших отверстий, через которые выходит воздух, нагнетаемый компрессором, внутрь дорожки. Струи воздуха, выходящие их этих отверстий, создают под тележкой воздушную подушку, которая позволяет тележке двигаться практически без трения. Дорожка снабжена оптическими датчиками, а тележка – выступами, которые прерывают световой поток в датчик. От датчиков сигнал поступает на интерфейс, измеряющий время на прерывании светового потока. Интерфейс соединен с компьютером, который измеряет кинематические характеристики тележки движущейся вдоль дорожки. В зависимости положения тележки от времени, скорости тележки от времени и ускорение тележки от времени.
Рис. 7. Временная диаграмма движения тележки
2. Четыре выступа, имеющиеся на тележке позволяют засекать момент времени t, в который тележка проходит мимо соответствующего датчика и измеряет два интервала времени между пересечениями двумя выступами оптического датчика. Расстояние между выступами Δx1 и Δx2 одинаковы. Таким образом, мы можем определить положение тележки в момент времени x(t):
где Δ t – время, за которое тележка проходят расстояние между серединами промежутков. Вывод: таким образом, мы независимо измеряем все кинематические характеристики движения тележки.
Ход работы На дорожке имеется ножка с микрометрическим винтом, который позволяет устанавливать и точно отсчитывать угол наклона дорожки. Создаем угол наклона 10–2 rad. Теперь мы сможем наблюдать движение тележки по наклонной дорожке, с углом наклона10–2 rad. Это означает что ускорение, которое мы должны получить будет составлять a = g·sinα ≈ 0,01g.
Проверим. 1. Теперь на экране наблюдаем зависимость координаты от времени для равноускоренного движения без начальной скорости (параболическая зависимость).
Рис. 9. Зависимость координаты от времени при равноускоренном движении
Среднее значение ускорения, вычисленное из этой кривой, составляет 0,096 м/с2, что соответствует тому значению, которое мы ожидали получить. 2. Зависимость скорости от времени при равноускоренном движении. Видно, что зависимость линейная с малым значением начальной скорости, причем среднее ускорение, вычисленное из угла наклона этой кривой, составляет 0,096 м/с2, как и в первом случае.
Рис. 10. Зависимость скорости от времени при равноускоренном движении 3. Зависимость ускорения от времени. Ошибки измерения ускорения несколько больше, чем у скорости, поэтому точки относительно среднего ускорения имеют небольшой разброс. Но среднее значение ускорения постоянно, и среднее арифметическое ускорения составляет 0,1 м/с2, что согласуется с теоретическим значением 0,098, полученным нами из наклона дорожки в пределах ошибок.
Рис. 11. Зависимость ускорения от времени при равноускоренном движении
Вывод: продемонстрировано равноускоренное движение, выявлены все требуемые зависимости.
Опыт 1.4 Падение тел Цель работы: рассмотреть независимость времени падения тел от величины горизонтальных составляющих и начальной скорости. Оборудование: 1. Стальные шары. 2. Горка. 3. Электромагнит.
Рис.12. Демонстрация опыта Ход работы 1. Один шар скатывается с горки, приобретает некоторую скорость в горизонтальном направлении 2. Шар начинает падение одновременно со вторым шаром, покоившимся в точке на линии, проведенной вдоль начальной скорости первого шара. Одновременность начала падения шаров обеспечивается тем, что первый шар в конце горки размыкает контакт в цепи питания электромагнита, удерживающего второй шар. 3. Далее шары, двигаясь по разным траекториям – по параболе и по прямой, но с одинаковым ускорением свободного падения g и одинаковой нулевой начальной скоростью в вертикальном направлении, оказываются одновременно в одном месте, то есть сталкиваются. Вывод: рассмотрели падение тел и узнали о независимости времени падения тел от величины горизонтальных составляющих и начальной скорости.
Опыт 1.5. Сложение движений Цель работы: изучить сложение движений на примере вращающегося диска с наблюдателями. Оборудование: 1. Вращающийся диск. 2. Мел.
Рис. 13. Демонстрация опыта
Ход работы Траектория тела зависит от того, в какой системе отсчета сидит наблюдатель. 1. Пусть будут два наблюдателя: один сидит на диске, а второй на неподвижной раме. 2. Если мы будем двигать кусок мела по диаметру, пока диск неподвижен, то траектория куска мела при его равномерном движении получается в виде прямой линии. 3. Но если наш диск будет вращаться, то траектория для неподвижного наблюдателя по-прежнему будет являться прямой линией, а для движущегося наблюдателя это будет уже совершенно другая линия – спираль Архимеда. Для неподвижного наблюдателя мел по-прежнему двигался по прямой линии, а для наблюдателя, сидящего на диске, мел совершил замысловатую кривую. Она получается в результате сложения двух движений: равномерного движения по радиусу вращающегося диска и равномерного вращения вокруг оси диска
Вывод: рассмотрели сложение движений на примере вращающегося диска с двумя наблюдателями. Узнали о спирали Архимеда, которая получается в результате сложения двух движений.
Недостаточно кинематически характеризировать движениеточки формой траектории, путем S и радиус-вектором Пусть материальная точка движется по криволинейной траектории. Вектор перемещения
Известно, что:
Для нахождения пути, пройденного телом за промежуток времени Δt, надо найти интеграл:
Скорость механического движения в большинстве случаев не остается постоянной, а меняется со временем либо по величине, либо по направлению, либо по величине и направлению одновременно. Приращение скорости
среднее ускорение
Используя предыдущие рассуждения, получим мгновенное ускорение:
Ускорение – физическая величина, характеризующая быстроту изменения скорости. Ускорение – вектор, равный производной от вектора скорости по времени и совпадающий по направлению с вектором изменения скорости dv за малый интервал времени dt. Легко показать, что
Зная кинематические уравнения движения, можно по аналогии получить:
а для модулей векторов скорости и ускорения:
Криволинейное движение В общем случае криволинейного неравномерного движения скорость изменяется как по величине, так и по направлению. Полное ускорение, которым обладает движущаяся точка, определяет оба вида изменения скорости. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости направлен всегда по касательной к траектории. Найдем вектор изменения скорости:
где Δv характеризует изменение скорости и по величине и направлению. Разложим Δv на две составляющие:
Относительное движение Системы отсчета можно связать как с неподвижными телами отсчета, так и с движущимися. Движение тела в подвижной системе – относительное движение. Движение тела в неподвижной системе – абсолютное движение. Движение тела относительно неподвижной системы отсчета, которым бы оно обладало, будучи жестко связанным одной из точек подвижной системы отсчета, называется переносным движением.
Преобразования ГАЛИЛЕЯ
Зная, что
Уравнения (27) и (28) в векторной записи в общем случае:
Из уравнения (30) следует, что ускорение одного и того же тела в каждый момент времени одинаково во всех системах отсчета, движущихся относительно друг друга равномерно и прямолинейно. Системы отсчета, движущиеся относительно неподвижной равномерно и прямолинейно, называются инерциальными. Следовательно, инерциальные системы отсчета образуют замкнутую систему. В некоторых задачах за инерциальные могут быть приняты системы, связанные с Землей или телами, движущимися, движущимися относительно Земли равномерно и прямолинейно. Равенство (7) выражает механический принцип относительности.
Уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой. Введение сил инерции дает возможность описывать движение тел в любых системах отсчета. Силы инерции не являются силами воздействия (упругие, гравитационные, трения), они обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления. Силы инерции – фиктивные силы.
Ход работы Демонстрируется распределение скоростей во вращающемся диске (точило), то есть в твердом теле. О величине и направлении линейной скорости различных точек вращающегося тела можно судить по длине и направлению снопа искр, возникающих при прижимании стальной проволоки к наждачному диску (точило). 1. Можно прижать стальную проволоку сразу в двух точках, и мы увидим, как скорости направлены в разных точках диска (точило). 2. Можно также продемонстрировать распределение скоростей вдоль радиуса вращающегося диска. На вертикальном радиусе мы видим, что величина снопа искр по мере удаления от оси вращения увеличивается, то есть скорость вращения возрастает. В нижней части диска, на вертикальном диаметре скорость направлена в противоположную сторону и так же возрастает по мере увеличения расстояния до оси. На горизонтальном диаметре происходит то же самое, но скорость уже направлена соответственно вверх и возрастает от оси, либо вниз и также возрастает по мере удаления от оси вращения. 3. Если теперь выключить мотор и остановить точило, касаясь его проволокой в одной точке, то мы увидим, что при уменьшении скорости длина снопа искр постепенно уменьшается. Вывод: рассмотрели распределение скоростей во вращающемся диске (точило). О величине и направлении линейной скорости различных точек вращающегося тела можно судить по длине и направлению снопа искр, возникающих при прижимании стальной проволоки к наждачному диску (точило). Ход работы Черный шар с белыми точками может приводиться в независимое вращение вокруг двух взаимно перпендикулярных осей – вертикальной и горизонтальной. Угловые скорости вращения вокруг каждой из осей регулируются от нуля до некоторой максимальной величины. Сложное движение твердого тела, то есть вращение одновременно вокруг двух осей, сводится к вращению вокруг мгновенной оси, которая движется и в пространстве и относительно тела. Вблизи мгновенной оси смазывание белых точек на черном шаре минимально, так как их скорости близки к нулю. Из-за перемещения мгновенной оси вращения легко следить по перемещению этих несмазанных точек: 1. Сначала мы раскрутили шар вокруг одной оси. 2. Затем постепенно увеличиваем скорость его движения вокруг второй оси, а первую скорость будем уменьшать. При этом мгновенная ось вращения пройдет все положения, от горизонтального до вертикального. 3. Затем опыт повторим в обратном порядке от вертикали до горизонтали. Особенно хорошо несмазанные точки видны при замедленном воспроизведении опыта. Вначале шар раскручен вокруг вертикальной оси, затем мы постепенно добавляем горизонтальную скорость вращения, а вертикальную уменьшаем и видим, как эти несмазанные точки постепенно перемещаются от вертикального диаметра шара к горизонтальному. При этом заметно, что шар не крутится вокруг одной какой-то точки, а эти точки постоянно меняются, то есть то не крутиться одна, то другая. То есть мгновенная ось вращения движется и относительно тела также.
Вывод: провели опыт с шаром с точками. Рассмотрели сложения угловых скоростей на примере этого шара.
При неравномерном вращения выражения для мгновенных значений ω и ε имеют вид:
где ε – угловое ускорение. Каждая точка твердого тела (например, точка А) движется по окружности радиуса r с линейной скоростью DS = RDφ, (35)
или dS = Rdφ, (36)
но
и
Дополнительные данные о вращательном движении: а) каждая точка твердого тела обладает нормальным ускорением an; б) полное ускорение:
в) связь частоты ν и периода Т:
г) Поскольку взаимное расположение элементов (точек) твердого тела не изменяется, для изучения его достаточно изучить движение одной его точки. Точка, движение которой эквивалентно движению твердого тела, массой М под действием результирующей внешних сил F, называется центр масс тела (центр инерции).
Вопросы к разделу 1 «Кинематика»
1. Дайте определение материальной точке. 2. Охарактеризуйте виды движения в зависимости от формы траектории. 3. Что называется вектором перемещения? 4. Перечислите оборудование для опыта 1.1 «Равномерное движение». 5. Перечислите оборудование для опыта 1.4 «Падение тел». Какой вывод следует из этого опыта? 6. Дайте определение мгновенной скорости. 7. По какой формуле можно найти путь, пройденный телом за промежуток времени ∆t? 8. Что называется ускорением? 9. Напишите формулы для вычисления среднего и мгновенного ускорений. 10. Какие системы отсчета называются инерциальными? 11. Сформулируйте принцип относительности Галилея. 12. Что называется твердым телом? 13. Какое движение называют поступательным? 14. Какое движение называют вращательным? 15. Какие выводы следуют из опыта с точилом? 16. Запишите формулы для вычисления угловой скорости, углового ускорения. 17. Запишите формулу, связывающую угловую и линейную скорости, угловое и тангенциальное ускорения. 18. Запишите формулу для вычисления полного ускорения. 19. Запишите формулу, связывающую частоту и период вращения. 20. Что называется центром масс тела?
ДИНАМИКА Ход работы При медленном надавливании железным стержнем на палочку она не сломается, Затем повторим опыт. Подвесим вновь палочку на двух целых кольцах. Затем резко ударим по ней металлическим стержнем. Наблюдаем, что палочка сломалась, а кольца остались прежними.
Вывод: при резком ударе части линейки приходят в движение, но оно не передается кольцам (очень мало времени), поэтому линейка переламывается, а кольца целы. Ход работы На вертикальной стойке имеется небольшая чашечка, в которой может помещаться стальной шарик. На нее кладется железная пластинка. При помощи пружинного ударника пластинка резко выбивается из-под шарика. При этом шарик за счет своих инертных свойств не успевает сдвинуться с места и падает точно в чашечку, находящуюся под ним.
Вывод: шарик за счет своих инертных свойств не успевает сдвинуться с места и падает точно в чашечку, находящуюся под ним.
Инерция тел проявляется также в том, что изменение движения тела под действием сил происходит не мгновенно, а протекает во времени.
Это основной закон динамики для поступательного движения.
Ход работы Дорожка с воздушной подушкой снабжена в конце двумя блоками – нижним и верхним. Эти блоки могут двигаться практически без трения. 1. К тележке присоединена нить, и на ней мы можем подвешивать грузик известной массы. Таким образом, можно проверить второй закон Ньютона. 2. Вначале мы будем осуществлять проверку при постоянной массе тележки и переменной силе натяжения нити, которая создается подвешиванием грузиков известной массы на нить. Начинаем мы с небольшой массы грузиков. 3. Запускаем тележку. 4. Затем постепенно увеличиваем массу грузиков и повторяем опыт. Таким образом, мы сможем, измеряя ускорение тележки, проверить, выполняется ли пропорциональность ускорения тележки силе натяжения нити.
Вывод: проверили справедливость второго закона Ньютона. Проверили выполнимость пропорциональности ускорения тележки силе натяжения нити.
Ход работы 1. Если мы перевернем магниты на левой чаше так, что сила отталкивания между ними сменится на притяжение и они притянутся друг к другу, то равновесие весов при этом не нарушится, что говорит о выполнении третьего закона Ньютона: внутренние силы не могут вызвать изменения положения равновесия этих весов. 2. Теперь то же самое можно проделать на правой чашке, используя внутреннюю силу Архимеда. Для этого мы опускаем пробирку в воду, при этом на нее будет действовать выталкивающая сила, но эта сила – внутренняя для данной системы, и равновесие весов также не будет нарушаться. 3. То, что сила действительно действует на пробирку, докажем, опуская другую пробирку, при этом внешнее равновесие нарушается.
Вывод: проверили справедливость третьего закона Ньютона. Внутренние силы не могут вызвать изменения положения равновесия.
Ход работы 1. Проверяем одинаковость масс тележек путем взвешивания. 2. Ставим тележки на рельсы на некотором расстоянии друг от друга. 3. Соединяем их ниткой. Тележки могут легко кататься по рельсам на колесиках, кроме того, остаточная сила трения при одинаковых массах тележек также должна быть одинакова. 4. Включаем мотор, нитка будет наматываться на вал, внутренняя сила взаимодействия между тележками, которая обеспечивается натяжением нити, будет одинакова по третьему закону Ньютона, тележки съедутся вместе и остановятся в центре картинки. При этом суммарный импульс системы остается равным нулю, и после сближения тележек они должны остановиться. Видим, что тележки съезжаются и останавливаются, что показывает справедливость третьего закона Ньютона: внутренние силы не могут изменить суммарный импульс системы.
Вывод: проверили справедливость третьего закона Ньютона. Внутренние силы не могут изменить суммарный импульс системы.
Ход работы С помощью линейки датчиков от воздушной дорожки можно провести измерения ускорения свободного падения и использовать для этого разные шарики – пластиковый, алюминиевый и стальной. Все шарики имеют одинаковые размеры, но разную массу. Бросая их поочередно в воздухе, можно получить из экстраполяции зависимости измеренного ускорения шариков значение ускорения свободного падения в вакууме. 1. Начинаем с пластикового шарика. 2. Затем бросаем алюминиевый шарик. 3. Затем бросаем стальной шарик. 4. Видим на экране график зависимости ускорения шариков от обратной величины их массы.
Рис. 29. Зависимость ускорения шариков от массы
5. Экстраполируя эту зависимость к бесконечной массе, мы получаем значение ускорения свободного падения в вакууме, поскольку при бесконечной массе шарика того же размера сопротивление воздуха не будет оказывать влияния.
Вывод: измерили ускорение свободного падения с помощью линейки датчиков от воздушной дорожки. Значение ускорение получилось (9,7980 ± 0,0006) м/с2, что с хорошей точностью согласуется со значением ускорения свободного падения. Ход работы На дорожке с воздушной подушкой можно исследовать не только движение тележки под воздействием постоянных сил, но и при наличии переменных сил, например, сил вязкого трения. 1. Силу вязкого трения проще всего реализовать, если установить на тележку постоянные магниты, которые при движении тележки по алюминиевому корпусу дорожки будут создавать вихревые токи – токи Фуко и, взаимодействуя с ними, будут создавать силу трения, пропорциональную скорости. 2. Сейчас дорожка установлена в строго горизонтальном положении, создадим начальный толчок тележки при помощи электромагнитного пускателя и посмотрим, как при этом будет двигаться тележка. 3. Запускаем тележку и видим, что она движется не с постоянной скоростью, а скорость ее постепенно уменьшается. 4. Закончив измерения, выведем на экран зависимости ускорения и логарифма ускорения от времени. Видим, что ускорение с течением времени убывает по модулю, поскольку оно отрицательно, а логарифм ускорения линейно зависит от времени. То есть зависимость ускорения от времени действительно экспоненциальная. 5. Теперь посмотрим зависимости скорости от времени и логарифма скорости от времени. Скорость с течением времени убывает по экспоненциальному закону, а логарифм скорости минус ее установившееся значение, которое близко к нулю, линейно зависит от времени. 6. Очевидно, что сила сопротивления при этом должна быть пропорциональна скорости.
Рис. 31. Зависимости ускорения и логарифма ускорения от времени
Рис. 32. Зависимости скорости и логарифма скорости от времени
Рис. 33. Зависимость силы сопротивления от скорости Сила сопротивления отрицательна и с ростом скорости увеличивается по линейному закону, причем поскольку дорожка была в горизонтальном положении, то внешняя сила равнялась нулю, а экспериментальное значение внешней силы, вычисленной нами из наших измерений, так же в пределах ошибок близко к нулю.
Вывод: исследовали движение тележки при наличии переменных сил, сил вязкого трения. Ускорение с течением времени убывает по модулю, скорость с течением времени убывает по экспоненциальному закону, сила сопротивления пропорциональна скорости.
Силы В современной физике различают четыре вида взаимодействий: 1) гравитационное (или взаимодействие, обусловленное всемирным тяготением), 2) электромагнитное (осуществляемое через электрические и магнитные поля), 3) сильное или ядерное (обеспечивающее связь частиц в атомном ядре) и 4) слабое (ответственное за многие процессы распада элементарных частиц). В рамках классической механики имеют дело с гравитационными и электромагнитными силами, а также с упругими силами и силами трения. Величина гравитационной силы определяется формулой (47):
Величина силы, с которой взаимодействуют два покоящихся точечных заряда q 1 и q 2, дается законом Кулона:
где k – коэффициент пропорциональности, зависящий от выбора единиц входящих в формулу величин. Если заряды движутся, то, кроме силы (48), на них действуют магнитные силы. Магнитная сила, действующая на точечный заряд q, движущийся со скоростью v в магнитном поле с индукцией В, определяется формулой F = k'q [ v, B ], (50) где k' – коэффициент пропорциональности). Понятие консервативных сил Если внутри системы, состоящей из нескольких материальных точек (тел), под действием силы Силы, работа которых не зависит от формы пути, а определяется только начальным и конечным положениями тела в пространстве, называются консервативными или потенциальными. Силы, работа которых зависит от формы пути, называются неконсервативными. Силы являются консервативными тогда, когда в системе нет перехода механического движения в другие формы движения материи или наоборот. Силы, работа которых возрастает по величине при увеличении пути, независимо от того, замкнут путь или нет, называются диссипативными. В этом случае механическая энергия переходит во внутреннюю, и работа этих сил определяется неоднозначно.
Вопросы к главе 2 «Динамика» Момент силы Вращательным моментом М (или моментом силы относительно оси) называется величина, равная произведению силы на плечо (плечо ℓ – кратчайшее расстояние от оси вращения до линии действия силы):
Если на тело действует n сил, то тело будет находиться в равновесии, если алгебраическая сумма моментов сил равна нулю. Момент силы – вектор, его направление связано с направлением действия силы правилом буравчика (правого винта):
где α – угол между векторами Момент инерции Момент инерции материальной точки:
Моментом инерции материальной точки относительно центра вращения называется величина, равная произведению массы точки на квадрат ее расстояния до центра вращения. Момент инерции J тела зависит: а) от формы тела; б) от размеров тела; в) от того, относительно какой оси вращается тело; г) от распределения массы по объему тела. Приведем моменты инерции тел правильной геометрической формы, выполненные из однородных материалов, и используемые при решении задач.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.75.227 (0.221 с.) |
 , (3)
, (3) – радиус-вектор, проведенный из начала координат в точку 1.
– радиус-вектор, проведенный из начала координат в точку 1. , проведенный из начала в конец положения движущийся точки, называется вектором перемещения.
, проведенный из начала в конец положения движущийся точки, называется вектором перемещения.
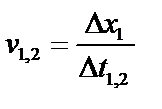 , (4)
, (4)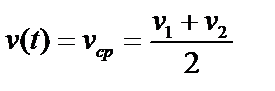 , (5)
, (5)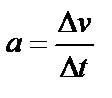 , (6)
, (6)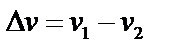 , (7)
, (7)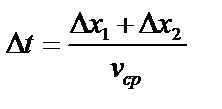 , (8)
, (8)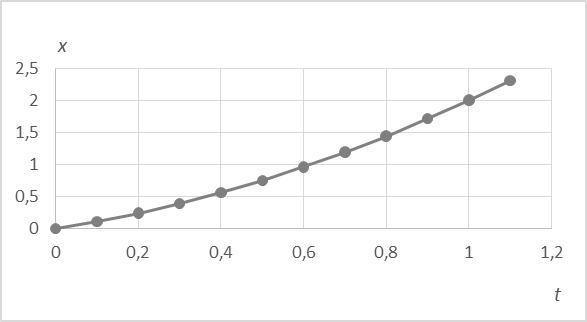


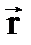 , надо указать быстроту перемещения.
, надо указать быстроту перемещения.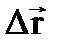 представляет приращение радиус-вектора
представляет приращение радиус-вектора 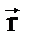 за время Δt:
за время Δt: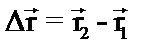 . (9)
. (9)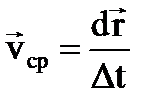 , (10)
где
, (10)
где 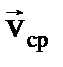 – средняя скорость движения.
Вектор
– средняя скорость движения.
Вектор 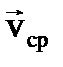 совпадает по направлению с
совпадает по направлению с 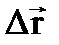 .
Мгновенная скорость, т.е. скорость в данный момент времени:
.
Мгновенная скорость, т.е. скорость в данный момент времени:
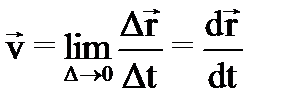 . (11)
. (11)
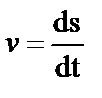 . (12)
. (12)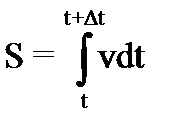 . (13)
. (13)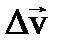 :
: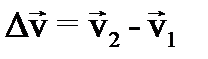 , (14)
, (14)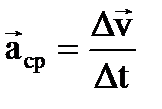 . (15)
. (15)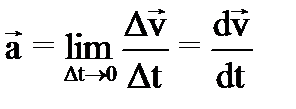 . (16)
. (16)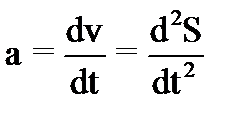 . (17)
. (17)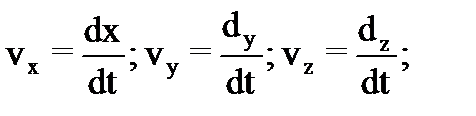 (18)
(18)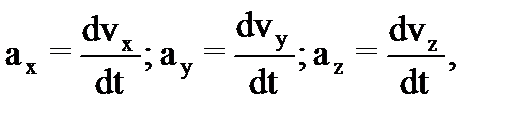 (19)
(19)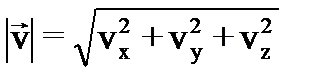 , (20)
, (20)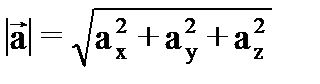 . (21)
. (21)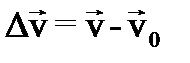 , (22)
, (22)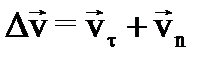 (23)
Учитывая, что
(23)
Учитывая, что
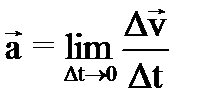 ,
имеем
,
имеем
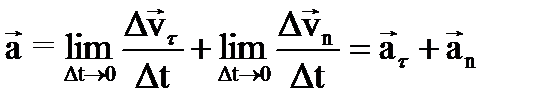 .
.
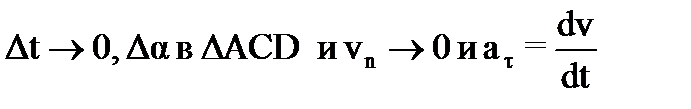 ;
2) при
;
2) при 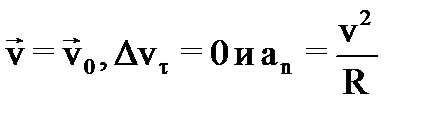 ;
3) модуль полного ускорения определяется как
;
3) модуль полного ускорения определяется как
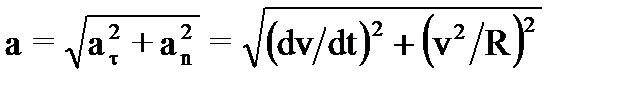 . (24)
Так как векторы ускорений
. (24)
Так как векторы ускорений 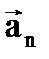 и
и 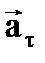 взаимно перпендикулярны, то:
взаимно перпендикулярны, то:
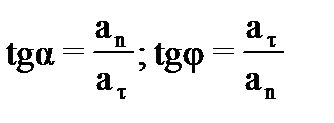 . (25)
Угол j определяет направление полного ускорения.
. (25)
Угол j определяет направление полного ускорения.
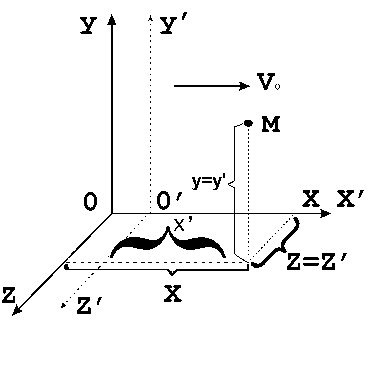 Рис. 17. Относительность движения
Рис. 17. Относительность движения
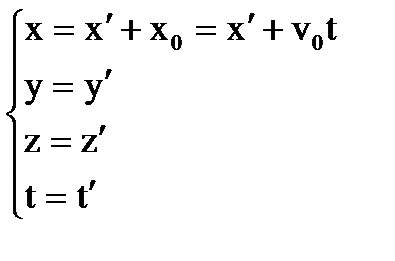 (26)
(26)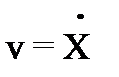 и
и 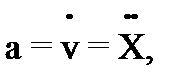 имеем:
имеем: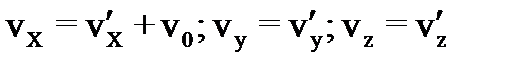 , (27)
, (27)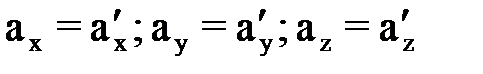 . (28)
. (28)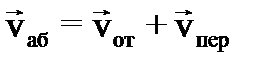 , (29)
, (29)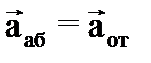 . (30)
. (30) Рис. 22. Вращение твердого тела вокруг неподвижной оси
Рис. 22. Вращение твердого тела вокруг неподвижной оси
 , (32)
где ωср – средняя угловая скорость тела.
Угловая скорость – вектор, имеющий направление правого винта и направлен по оси вращения.
, (32)
где ωср – средняя угловая скорость тела.
Угловая скорость – вектор, имеющий направление правого винта и направлен по оси вращения.
 (33)
(33)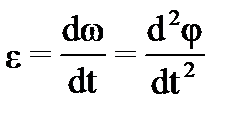 , (34)
, (34) . Тогда за время Dt тело переместится на:
. Тогда за время Dt тело переместится на: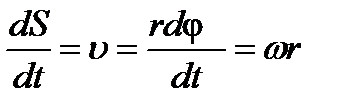 , (37)
, (37) (38)
(38) , (39)
, (39) . (40)
. (40) ; (41)
; (41) ; (42)
; (42) . (43)
. (43) (46)
(46)
 (47)
(47)



 . (48)
. (48) , (49)
, (49) происходит перемещение тела относительно других тел из одного произвольного положения в другое, то работа A1,2, совершаемая при этом, не зависит от формы пути перехода.
происходит перемещение тела относительно других тел из одного произвольного положения в другое, то работа A1,2, совершаемая при этом, не зависит от формы пути перехода. . (51)
. (51) ,
, , (52)
, (52) и
и  .
. . (53)
. (53)


