
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная погрешность приближенного значения величины. Граница абсолютной погрешности.Стр 1 из 9Следующая ⇒
Абсолютная погрешность приближенного значения величины. Граница абсолютной погрешности. Числа, полученные в результате измерения лишь приблизительно с некоторой точностью характеризует искомую величину. Х – это точное значение величины; а – это приближенное значение вылечены. Если, а ≤ х – приближенное значение с недостатком (приближение с низу). Если, а ≥х – приближенное значение с избытком (приближение с верху). Разность точного и приближенного значения величины называют – погрешностью приближения (х-а). ïx-aï - абсолютная погрешность приближения а - ∆х ≤ х ≤ а +∆х. Во многих случаях нельзя найти абсолютную погрешность приближения, т.к. неизвестно точное значение пелесины. Однако можно указать положительное число, больше которого эта абсолютная погрешность быть не может. Любое положительное число, которое больше или равно абсолютной погрешности называется – границей абсолютной погрешности (∆х≤h; x» a с точностью до h; x=a+-h). Относительная погрешность и граница относительной погрешности. Отношение абсолютной погрешности приближается к модулю приближенного значения величины называется – относительной погрешности приближения и выражается в %. ∆x/ïaï*100% - относительная погрешность. ïx-aï/ïaï*100% Любое положительное число, которое больше или равно относительной погрешности называется границей относительной погрешности => ∆x/ïaï≤δ; h/ïaï=δ; h=δïaï. Цифры верные в широком смысле, верные в строгом смысле. Цифра m приближенного числа a называется верной в широком смысле, если граница абсолютной погрешности числа а не превысит единицы того разряда в котором записана цифра n. Цифра m приближенного числа a называется верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда в котором записана цифра n. В цифрах полученных в результате измерений или вычислений и используемых при расчетах, а так же в десятичной записи приближенного числа все цифры должны быть верными. Те цифры, о которых неизвестно являются ли они верными называют сомнительными. Метод Хорд. F(x)=0, f(x) – непрерывная функция имеющая на интервале a,b производные первого и второго порядка. Идея метода состоит в том что на достаточно малом отрезке a,b дуга кривой y=f(x) заменяется касательной к этой кривой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Ox. 1случай: 1ая и 2ая производные функции f(x) имеют одинаковые знаки: f‘(x)*f’’(x)>0. записываем ура-е хорды как уравнение прямой через 2 точки: x-x1 / x2 –x1 = y-y1 / y2-y1. Формула: xn+1 = xn – f(xn) / f’(xn), х1=б-ф(б)/ф'(б). Получаем последовательность приближенных значений, в которой каждый последующий член ближе к приближенному значению корня и при этом получается приближенное значение с избытком. 2 случай: разные знаки формула такая же но с (а). Получаем последовательность приближенных значений с недостатком. При выборе начального приближения необходимо следовать правилу: За исходную точку следует выбрать тот конец отрезка (а,б), в котором знак функции совпадает со знаком 2ой производной. Если производная функция на отрезке (а,б) мало изменяется, то можно пользоваться формулой: xn+1 = xn – f(xn) / f’(x0). В вычислениях по этой формуле производная считается один раз.
10. Метод касательных. Приближенный метод решений. Процесс нахождения приближенных значений корней уравнения разбивается на 2 этапа:
1. определение корней – разбить всю обл. допустимых значений на отрезке в каждом из которых содержится 1 корень. 2. уточнение корней до заданной степени точности. Порядок действий при отделении корней. 1. находят 1вую производную f ’(x); 2. составляют табл. знаков функции x=: а) корням производной или числа ближайшими к ним б) граничными значениями из обл. допустимых значений; 3. определяют интервалы на концах которых фун-ия принимает значение противоположных знаков.
Формула трапеций. bòa f(x)dx» h/2(y0+y1) криволинейная трапеция заменяется трапецией, а под интегральная функция заменяется интерпаляционым многочленом Лагранжа 1ой степени. Линейная интерполяция: bòa f(x)dx» ((b-a)/h)/((y0+yn)/2)+y1+y2+…+yn-1 23. Постановка задачи численного решения Д.У.
21. Формула Симпсона. Если заменить график функции f(x) на каждом участке отрезка дугами парабол, то получим формулу для вычисления интеграла bòa f(x) dx более точную, чем формула прямоугольников и трапеций. Формула Симпсона bòa f(x) dx» ((a-b)/bh)/((y0+y2n)+4(y1+y3+…+y2n-1)+2(y2+y4+…+y2n-2)) Формула дает точное значение интеграла в тех случаях, когда f(x) многочлен, степень которого меньше или равно 3, т.к. в этом случае производная 4 порядка = 0.
Метод Пикара решения Д.У. Позволяет получить приближённое знач. ДУ y’=f(x,y) в виде ф-и, представленной аналитически. Пусть в условиях теоремы существования требуется найти решение уравнения y’=f(x,y) с начальным условием y(x0)=y0. Проинтегрируем обе части уравнения y’=f(x,y) от х0 до х или Решение ИУ будет удовлетворять ДУ и начальному условию. При х=х0 получим: ИУ позволяет позволяет применить метод последовательных приближений. Будем рассматривать правую часть ф-лы как оператор, отображаущий всякую ф-ю в другую ф-ю того же класса Если этот опратор является сжимающим, то можно строить последовательность приближений, сходящуюся к точному решению. В качестве начального приближения принимается y=(x)=y0, и находится первое приближение Интеграл в правой части содержит только переменную х, после нахождения этого интеграла будет получено аналитическое выражение приближения y1(x) как ф-и переменной х. Далее заменим в правой части ур. у найденным значением y1(x) и получим второе приблидение и т.д. В общем случае итерационная формула имеет вид Циклическое применение формулы даёт последовательность ф-й y0 y1 yn сходящуюся к решению интегрального уравнения (6.7) (а, следовательно, и дифференциального уравнения (6.1) с начальными условиями (6.2)). Это также означает, что к-й член последовательности (6.9) является приближением к точному решению уравнения (6.1) с определенной контролируемой степенью точности. Оценка погрешности k-го приближения дается формулой где y(x)- точное решение N определяется равенстовом, M-константа Липшица из неравентсва Метод Эйлера решения Д.У. 1)Универсальный численный метод решения д.у. – метод конечных разностей. Сущность – замена области непрерывного измерения аргумента дискретным множеством точек (сеткой или сеточной области с постоянным или переменным шагом h).
Аппроксимация д.у.
2) Решить дифференциальное уравнение у/=f(x,y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0. Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования. Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов. Рассмотрим дифференциальное уравнение первого порядка y/=f(x,y) (1) с начальным условием x=x0, y(x0)=y0 (2)
Метод Рунге-Кутта. Широкая категория методов, наиболее часто применяемых на практике для решения дифференциальных уравнений, известна под общим названием: методы Рунге - Кутта. Различные методы этой категории требуют большего или меньшего объема вычислений и, соответственно, обеспечивают большую или меньшую точность. Методы Рунге - Кутта обладают следующими отличительными свойствами: эти методы являются одноступенчатыми: чтобы найти значение функции в точке yi +1 нужна информация только о предыдущей точке (yi, xi); они согласуются с рядом Тейлора вплоть до членов порядка hk, где степень k определяет порядок метода; эти методы не требуют вычисления производных от f (x, y), а требуют вычисления самой функции. Именно благодаря последнему свойству методы Рунге - Кутта более удобны для практических вычислений. 32. Решение транспортной задачи методом потенциалов.
30. Транспортная задача.
Модели управления запасами. Задача управления запасами возникает, когда необходимо создать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени. Для обеспечения непрерывного и эффективного функционирования практически любой организации необходимо создание запасов. В любой задаче управления запасами требуется определить количество заказываемой продукции и сроки размещения заказов. В любой задаче управления запасами требуется определить количество заказываемой продукции и сроки размещения заказов. Спрос можно удовлетворить путем однократного создания запаса на весь рассматриваемый период времени или посредством создания запаса для каждой единицы времени этого периода. Эти два случая соответствуют избыточному запасу (по отношению к единице времени) и недостаточному запасу (по отношению к полному периоду времени). При избыточном запасе требуются более высокие удельные (отнесенные к единице времени) капитальные вложения, но дефицит возникает реже и частота размещения заказов меньше. При недостаточном запасе удельные капитальные вложения снижаются, но частота размещения заказов и риск дефицита возрастают. Для любого из этих двух крайних случаев характерны значительные экономические потери. Таким образом, решения относительно размера заказа и момента его размещения могут основываться на минимизации соответствующей функции общих затрат, включающих затраты, обусловленные потерями от избыточного запаса и дефицита. Критерии игры с «природой». В матричных играх предполагается участие 2-х игроков с противоположными интересами, а в некоторых задачах, приводящих к игровым, есть неопределённость, вызванная отсутствием информации об условиях, в которых происходит действие. Эти условия зависят не от действий игроков, а от объектной действительности (погода, покупательский спрос).
Такие игры называют игры с «природой». Человек в играх с природой старается действовать осмотрительно. А второй игрок- природа, действует случайно. Задается матрица mn и имеется ряд критериев, которые имеют значение при выборе оптимального решения. 1.Критерий Вальде – рекомендуется применять максимальную стратегию. Совпадает с нижней ценой игры. Критерий пессимистический, т.к. считается, что природа будет действовать наихудшим для человека образом. 2.Критерий максимизма max max aij. Критерий оптимистический, считается что природа будет действовать наилучшим для человека образом. 3.Критерий Гурвина – 4. Критерий Сэвиджа. Суть состоит в выборе такой стратегии, которая не допускает чрезмерно высоких потерь. Находят матрицу рисков, элементы которых показывают какой убыток, понесёт человек или фирма, если для каждого состояния природы, он не выберет наилучшую стратегию. rij=max aij-aij элементы матрицы рисков min {max(maxaij-aij)} или min rij Симплекс-метод. Симплексный метод – итеративный процесс направленного решения сист. уравн. по шагам, которое нач. с опорного решения и в поисках лучшего варианта движется по условным т. обл. допустимого решения, улучшая значения целевой ф. до тех пор, пока она не достигает своего максимального или мин. значения.
Абсолютная погрешность приближенного значения величины. Граница абсолютной погрешности. Числа, полученные в результате измерения лишь приблизительно с некоторой точностью характеризует искомую величину. Х – это точное значение величины; а – это приближенное значение вылечены. Если, а ≤ х – приближенное значение с недостатком (приближение с низу). Если, а ≥х – приближенное значение с избытком (приближение с верху). Разность точного и приближенного значения величины называют – погрешностью приближения (х-а). ïx-aï - абсолютная погрешность приближения а - ∆х ≤ х ≤ а +∆х. Во многих случаях нельзя найти абсолютную погрешность приближения, т.к. неизвестно точное значение пелесины. Однако можно указать положительное число, больше которого эта абсолютная погрешность быть не может. Любое положительное число, которое больше или равно абсолютной погрешности называется – границей абсолютной погрешности (∆х≤h; x» a с точностью до h; x=a+-h).
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.179 (0.032 с.) |

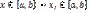



 - степень оптимизма,
- степень оптимизма, 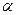 принадлежит отрезку [0;1]. Критерий промежуточной - учитывает как наихудшее, так и наилучшее поведение природы.
принадлежит отрезку [0;1]. Критерий промежуточной - учитывает как наихудшее, так и наилучшее поведение природы. 


