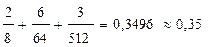Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шестнадцатиричная система счисления
Основание системы счисления (p) равно шестнадцати. В этой системе счисления используется шестнадцать цифр. Эту систему счисления можно считать еще одним вариантом записи двоичного числа. В шестнадцатеричной системе счисления уже не хватает десяти цифр, поэтому дополнительно были введены шесть символов. Для обозначения этих цифр используются шесть первых букв латинского алфавита. При записи шестнадцатеричного числа неважно буквы верхнего или нижнего регистра будут использоваться в качестве цифр. Таким образом, в качестве цифр в шестнадцатеричной системе используются следующие символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Так как в шестнадцатеричной системе счисления появляются новые цифры, то приведем таблицу соответствия цифр этой системы их десятичным эквивалентам. В табл. 5.3 в левом столбце приведены шестнадцатеричные символы, а справа — их десятичные эквиваленты. Таблица 5.3. Таблица соответствия шестнадцатеричных цифр десятичным значениям
Число в этой системе счисления записывается как сумма единиц, чисел шестнадцать, двести пятьдесят шесть и так далее. То есть веса соседних разрядов различаются в шестнадцать раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как шестнадцатые, двести пятьдесят шестые и так далее доли единицы Рассмотрим пример записи шестнадцатеричного числа:
Приведем таблицы операций сложения и умножения в шестнадцатеричной системе счисления. Д ля иллюстрации действий в шестнадцатеричной системе счисления выполним несколько операций. В качестве примера возьмем те же самые числа, что и в предыдущем случае, а именно 510 и 3,510. Сначала преобразуем их в шестнадцатеричную форму: A = 510 = 516. B = 3,510 = 3,816 = 3×160 + 8×16-1 = 310 + Таблица 5.4. Таблица сложения шестнадцатеричных чисел
Таблица 5.5. Таблица умножения шестнадцатеричных чисел
Затем выполним суммирование этих чисел в шестнадцатеричной системе счисления. В результате суммирования ожидаем получить число 8,510. Суммирование будем выполнять в "столбик". Так будет легче понять арифметические действия.
Для проверки переведем получившийся при выполнении операции суммирования результат в десятичную форму: 8,816 = 8×160 + 8×16-1 = 810 + 0,510 = 8,510 Как видно из полученного десятичного числа результаты совпадают. То есть при выполнении суммирования в шестнадцатеричной системе счисления ошибки не произошло. Теперь выполним операцию шестнадцатеричного вычитания. Вычтем из числа 510 число 3,510. В результате выполнения этой операции мы ожидаем получить десятичное число 1,5.
При вычитании разряда шестнадцатых частей сразу же возникает необходимость "заема" из старшего разряда. Если из единицы вычесть число 0,816, то в качестве результата получим тоже число 0,816. Записываем на место шестнадцатых частей цифру восемь. В разряде единиц из оставшейся после "заема" цифры 4 вычтем цифру 3. Проверим полученный результат. Для этого преобразуем число из шестнадцатеричной формы в десятичную: 1,816 = 1×160 + 8×16-1 = 110 + 0,510 = 1,510 Выполним операцию шестнадцатеричного умножения. Умножать будем те же самые числа (510 и 3,510). В результате операции умножения мы ожидаем получить число 17,510. Умножение произведем в "столбик". Умножение в столбик в шестнадцатеричной системе счисления выполняются точно так же как и в десятичной системе.
Первое частичное произведение образуется при умножении младшего разряда множителя на множимое. При умножении цифры 8 на цифру 0 получаем 0. Записываем младший разряд частичного произведения. Результат умножения цифры 8 на цифру 5 определяем по табл. 5.5. Точно так же получаем и второе частичное произведение, сдвигаем его на один шестнадцатеричный разряд (как в десятичной системе счисления) и точно так же как и в десятичной системе счисления в конце операции умножения суммируем все частичные произведения. Снова проверяем полученный результат. Для этого преобразуем число из шестнадцатеричной формы в десятичную: 11,816 = 1×161 + 1×160 + 8×16-1 = 1610 + 110 + 0,510 = 17,510 Из приведенных примеров записи чисел в различных системах счисления вполне очевидно, что для записи одного и того же числа с одинаковой точностью в разных системах счисления требуется различное количество разрядов. Чем больше основание системы счисления, тем меньшее количество разрядов требуется для записи одного и того же числа. Преобразование чисел из одной системы счисления в другую При проектировании цифровых устройств достаточно часто требуется уметь переводить число из одной системы счисления в другую. Давайте научимся выполнять такие действия. Преобразование целых чисел и правильных дробей выполняется по разным правилам. В действительном числе преобразование целой и дробной части производят по отдельности. Преобразование целой части числа Для преобразования целочисленного значения необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы, и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.
Рассмотрим для примера перевод числа из десятичной системы счисления в двоичную. Возьмем десятичное число А10 = 124 и поделим его на основание двоичной системы, то есть на число 2. Деление будем производить "уголком", как показано на рис. 5.1. В результате первого деления получим разряд единиц (самый младший разряд). В результате второго деления получим разряд двоек. Деление продолжаем, пока результат деления больше двух. В конце операции преобразования получили двоичное число 11111002:
Рис.5.1. Перевод числа из десятичной системы счисления в двоичную Для того, что бы проверить, нет ли ошибки, преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения: 1×26+1×25+1×24+1×23+1×22+0×21+0×20=6410+3210+1610+810+410=124 Теперь то же самое число переведем в восьмеричную систему счисления. Для этого число 12410 будем делить на число 8, как показано на рис. 5.2.
Рис.5.2. Перевод числа из десятичной системы счисления в восьмеричную Как видим, остаток от первого деления равен 4. То есть младший разряд восьмеричного числа содержит цифру 4 (единицы). Остаток от второго деления равен 7. то есть второй разряд восьмеричного числа — это цифра 7. Старший разряд получился равным 1. То есть в результате многократного деления мы получили восьмеричное число 1748. Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения: 1×82+7×81+4×80=6410+5610+410=124 А можно ли осуществить перевод из восьмеричной системы счисления в двоичную делением? Можно! Но деление нужно произвести по правилам восьмеричной арифметики. Правила работы в восьмеричной системе счисления мы рассмотрели в предыдущей главе. Рассмотрим пример перевода в двоичную форму полученного ранее восьмеричного числа 1748. Разделим его на основание новой системы счисления 2, как показано на рис. 5.3:
Рис.5.3. Перевод в двоичную форму восьмеричного числа Как мы убедились, выполнять деление в восьмеричной системе очень неудобно, ведь подсознательно мы делим в десятичной системе счисления. Если обратить внимание на то, что число 8 является степенью числа 2, то можно считать восьмеричную систему счисления просто более короткой записью двоичного числа. Это означает, что для представления восьмеричной цифры можно использовать три двоичных бита (8=23). Составим таблицу соответствия для такого преобразования.
Таблица 5.6. Таблица соответствия восьмеричных цифр и двоичного кода
Используя эту таблицу можно просто заменить каждую восьмеричную цифру тремя двоичными битами. Три двоичных бита обычно называют триадой или трибитом. Теперь переведем восьмеричное число 1748 в двоичную форму при помощи табл. 5.6, как показано на рис. 5.4:
Рис.5.4. Перевод восьмеричного числа в двоичную форму Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя табл. 5.6, каждой триаде ставят в соответствие восьмеричную цифру. Аналогичным образом можно выполнить перевод числа из шестнадцатеричной формы в двоичную и обратно. В этом случае для представления шестнадцатеричной цифры потребуется четыре двоичных разряда. Четыре двоичных разряда обычно называют тетрадой. Иногда при переводе иностранной литературы используется термин нибл. Составим таблицу соответствия двоичных тетрад и шестнадцатеричных цифр. Для этого будем просто прибавлять единицу к значению предыдущей строки в каждом столбце таблицы, в соответствии с используемой в этом столбце системой счисления. Результат приведен в табл. 5.7. В качестве примера использования табл. 5.7 переведем шестнадцатеричное число 7С16 в двоичную форму представления, как показано на рис. 5.5:
Рис.5.5. Перевод шестнадцатеричного числа в двоичную форму Таблица 5.7. Таблица соответствия шестнадцатеричных цифр и двоичного кода
Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму приведен на рис. 5.6.
Рис.5.6. Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму На этом рисунке внизу выделены двоичные тетрады и соответствующие им шестнадцатеричные цифры. Их соответствие можно проверить при помощи табл. 5.7. Сверху выделены триады и соответствующие им восьмеричные цифры. Старшая триада получилась неполной. Для того чтобы можно было бы воспользоваться табл. 5.6 ее необходимо дополнить старшими незначащими нулями Преобразование дробной части числа Так как дробная часть числа меньше единицы, то ее преобразование выполняется умножением исходного числа на основание новой системы счисления. Целая часть результата умножения будет старшим разрядом числа в новой системе счисления. Дробную часть произведения снова умножают на основание системы счисления. Операция умножения выполняется до достижения требуемой точности результата. Все операции выполняют по правилам исходной системы счисления.
Для примера рассмотрим перевод дробного числа из десятичной системы счисления в двоичную. Пусть исходное число A будет равно 0,35. Выполним операцию последовательного умножения, как это показано на рис. 5.7.
Рис.5.7. Пример операции последовательного умножения В результате описанных действий получим двоичное представление числа A: A = 0,3510» 0,01011=0,34375 В общем случае перевод правильных дробей является приблизительным. Число разрядов в новой системе можно найти исходя из одинаковой точности представления чисел в разных системах счисления. Одинаковая точность числа, записанного в различных системах счисления, достигается при одинаковых весах младших разрядов соответствующей системы счисления. Определить вес младшего разряда числа можно по следующей формуле: M =q -n, где q — основание системы счисления. В предыдущем примере для десятичного числа 0.35 вес младшего разряда M = 1/100 = 0.01. В полученном двоичном числе вес младшего разряда будет равен 1/32» 0,03. То есть при операции преобразования числа в двоичную форму мы ухудшили точность представления числа в три раза. Для одинаковой точности представления чисел в различных системах счисления необходимо выполнить равенство:
где p и q — основания старой и новой систем счисления соответственно. Для определения необходимого количества разрядов в новой системе счисления возьмем логарифм по основанию (p) от этого равенства:
откуда найдем требуемое количество разрядов:
Определим необходимое число разрядов в двоичной системе счисления для рассмотренного ранее примера:
В использованном нами примере количество разрядов десятичного числа после запятой n 10 = 2, то есть в двоичной системе счисления для той же точности числа количество разрядов должно быть равно:
Если же требуется обеспечить точность представления числа до трех разрядов после запятой n 10 = 3, то количество двоичных разрядов должно быть не менее:
Определим формулы пересчета количества разрядов, требующихся для записи числа в восьмеричной и шестнадцатеричной системе счисления:
В рассмотренном выше примере для записи десятичного числа 0,3510 в восьмеричной форме с той же точностью по этой формуле потребуется три разряда. Проверим это утверждение:
Аналогичным образом можно осуществлять перевод в любую систему счисления. Исключением является перевод из двоичной системы счисления в восьмеричную или шестнадцатеричную. Напомним, что эти системы счисления являются краткой записью двоичного числа, поэтому в этом случае можно переводить числа из одной системы счисления в другую при помощи таблиц перехода 5.6 и 5.7. Двоичное число разбивается на триады для перевода в восьмеричную систему счисления или на тетрады для перевода в шестнадцатеричную систему счисления. Разбиение начинается от двоичной запятой.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.213.209 (0.044 с.) |



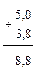
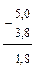








 ,
, ,
,



 ,
,