
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальный закон распределения.
Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами μ, σ2, если ее плотность распределения имеет вид
Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону равна параметру μ этого закона, а ее дисперсия – параметру σ2, т.е. М(X) = μ, D(X) = σ2. Таким образом, нормальное распределение f(x) случайной величины Х характеризуется двумя параметрами: μ - средним значением и σ2- дисперсией. Это обозначается как X ~ N (μ; σ2). График плотности нормального распределения имеет колоколообразный вид, симметричный относительно центра распределения
Максимум этой функции находится в точ ке x = m, а разброс относительно этой точки определяется параметром s2. Чем меньше значение s2, тем более острый и высокий максимум f(x). Нормальный закон распределения случайной величины Х с параметрами μ = 0, σ2 = 1называется стандартным нормальным распределением. Плотность стандартного нормального распределения есть
Любое нормальное распределение f(x) с параметрами μ, σ2 с помощью линейного преобразования t = (x – μ)/σ сводится к стандартному нормальному распределению f(t) с центром в нуле и единичной дисперсией, при этом f(x) = f(t)/σ, и f(x)dx = f(t)dt. Площадь под кривой стандартного нормального распределения f(t)/ в интервале (-t; t) обозначается как Ф(t) и называется функцией Лапласа, т.е. Ф(t) = Функции f(t), Ф(t) табулированы. Вычислим функцию распределения случайной величины Х, распределенной по нормальному закону: F(x) = Таким образом, F(x) = Геометрически, функция распределения F(x) представляет собой площадь под нормальной кривой f(x) на интервале (-∞; х). Замечание. В Excel имеются функции f(x) = НОРМРАСП(x; μ; σ; 0), F(x) = НОРМРАСП(x; μ; σ; 1), x = НОРМОБР(F; μ; σ).
Свойства нормального распределения. 1. Вероятность попадания нормальной случайной величины Х в интервал (х1,х2) есть
2. Вероятность отклонения нормальной случайной величины Х от среднего μ по модулю меньше Δ > 0, есть
Пример. Случайная величина Х распределена по нормальному закону с параметрами μ = 5, σ = 0,4. Найти: а) вероятность P(1 < X < 6,1); б) интервал, симметрично расположенный относительно среднего значения, в который с вероятностью 0,98 попадет Х.
▼ а) P(1 < X < 6,1) = б) t = 2,33 (по таблице). Из уравнения Симметричный интервал относительно среднего определяется неравенством: |х - 5| < 0,932, или 4,068 < X < 5,932. Упражнение. 1. Поезда метрополитена идут регулярно с интервалом 2 мин. Какова вероятность, что ждать пассажиру не больше полминуты. Найти математическое ожидание и дисперсию случайной величины Х – время ожидания поезда. Отв. 0,25; М(Х) = 1 мин.; D(X) = 1/3. 2. Среднее время обслуживания покупателя 20 мин. Чему равна вероятность простоя в очереди от 20 до 40 мин. Отв. 0,23. 3. Случайная величина Х распределена по нормальному закону с параметрами μ = 30, σ2 = 100. Найти вероятность того, что Х примет значение из интервала (10; 50). Отв. 0,9545. 4. Случайная величина Х распределена по нормальному закону с параметрами μ = 20, σ = 10. Найти вероятность того, что отклонение этой величины от средней по абсолютной величине будет меньше 5. Отв. 0,3829.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.102.225 (0.004 с.) |


 .
. .
.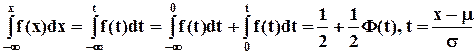 .
. , где
, где  .
. , где
, где 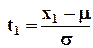 ,
,  .
. .
.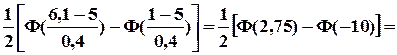 =
= 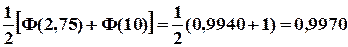 .
. . Обозначим
. Обозначим  . По условию Ф(t) = 0,98 Þ
. По условию Ф(t) = 0,98 Þ Þ Δ = 2,33∙0,4 = 0,932.
Þ Δ = 2,33∙0,4 = 0,932.


