
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы комбинаторики (с повторениями)Стр 1 из 14Следующая ⇒
Правила комбинаторики. Пусть имеется совокупность объектов. Правило суммы. Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбрать «либо А, либо В» можно m + n способами. Выбор «либо А, либо В» - взаимно исключающие действия. Пример. Сколькими способами можно выбрать одну четную или одну нечетную цифру из чисел 1, 2, 3, 4, 5. ▼ Четную цифру можно выбрать 2 способами, а нечетную – 3 способами. Тогда выбрать четную или нечетную цифру можно 2 + 3 = 5 способами. Правило произведения. Если объект А можно выбрать m способами и после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А, В) в указанном порядке можно осуществить mn способами. Пример. Сколькими способами можно выбрать одну четную и одну нечетную цифру из чисел 1, 2, 3, 4, 5. ▼ Четную цифру можно выбрать 2 способами, а нечетную – 3 способами. Тогда выбрать четную и нечетную цифру можно 2∙3 = 6 способами.
n! (n – факториал). По определению n! = 1∙2∙…∙n, причем 0! = 1. Например. 4! = 1∙2∙3∙4 =24, (10 – 7)! = 6,
Формулы комбинаторики (без повторений). Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества из m элементов, 0 ≤ m ≤n, по определенным правилам. Перестановки (m = n, порядок важен). Перестановками называется комбинации из n различных элементов, отличающихся друг от друга только порядком следования элементов. Число всех перестановок из n элементов обозначается Рn и определяется выражением: Рn = n!. ▼ Рассмотрим n клеток
В 1 – ую клетку можно поместить любой из n объектов, т.е разместить n способами, во 2 – ую клетку можно поместить любой из оставшихся (n – 1) объектов, т.е. можно разместить (n – 1) способами и т.д.; в последнюю клетку можно поместить только 1 объект. Согласно правилу произведения, разместить n объектов в n клетках можно n(n-1)∙∙∙1 = n! способами. Пример. Сколькими способами можно расставить 6 различных книг на одной полке. ▼ n = 6, m = 6, (m = n, порядок важен), Рn = 6! = 720. Замечание. В Excel имеется функция Рn = ПЕРЕСТ(n; n).
Размещения (m ≤ n, порядок важен). Размещениями называется комбинация из n различных элементов по m, отличающихся друг от друга либо самими элементами, либо порядком следования элементов. Число всех размещений из n элементов по m обозначается
▼ Рассмотрим m клеток
Согласно правилу произведения, разместить из n элементов в m клетках можно n(n-1)∙∙∙(n – (m – 1)) = При m = n размещения совпадают с перестановками. Замечание. В Excel имеется функция Пример. Сколькими способами можно выбрать из 10 студентов старосту и дежурного. ▼ n = 10, m = 2, (m < n, порядок важен),
Сочетания (m ≤ n, порядок не важен). Сочетаниями называется комбинация из n различных элементов по m, отличающихся друг от друга только самими элементами. Число всех сочетаний из n элементов по m обозначается ▼ Чтобы получить Замечание. В Excel имеется функция Свойства комбинаций: Пример. Сколькими способами можно выбрать из 10 студентов двух дежурных. ▼ n = 10, m = 2, (m < n, порядок неважен), Упражнение. 1. Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если не одна из цифр не повторяется более одного раза. Отв. 300. 2. Сколькими способами можно составить команду из 4 человек для соревнования по бегу, если имеется 7 бегунов. Отв. 35. 3. В конкурсе участвуют 10 фирм, среди которых жюри должна выбрать 3 фирмы на 1, 2, 3 – место, Сколько способов награждения у жюри существует. Отв. 720. 4. Абонент забыл последние три цифры телефонного номера. Какое наибольшее число вариантов номеров ему нужно набрать, если известно, что цифры различны. Отв. 720. 5. В группе 10 футбольных команд. Сколько матчей нужно провести, чтобы каждая команда сыграла с каждой. Отв. 45. 6. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно. Отв. 5040. 7. В урне 5 красных, 4 синих и 3 зеленых шара. Сколькими способами из урны можно вынимать наугад 3 шара, чтобы а) все шары оказались красными. Отв. 10; б) все шары оказались синими. Отв. 4;
в) все шары оказались зелеными. Отв. 1; г) все шары оказались одного цвета. Отв. 15; д) все шары оказались разного цвета. Отв. 60; е) два шара оказались красными, а один синим. Отв. 40; ж) два шара оказались красными, а один зеленым. Отв. 30; з) два шара оказались красными. Отв. 70; и) хотя бы два шара оказались красными. Отв. 80. 8. Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более пяти, а во второй – не более девяти человек. Отв. 1507.
В n независимых испытаниях
I. Теорема. Математическое ожидание числа появления событий в одном испытании равно вероятности р этого события, а дисперсия - произведению pq, т.е. М(Х) = р, D(X) = pq. ▼ Пусть производится 1 испытание, в котором вероятность события А равно р. Случайная величина Х (число появления события А в одном испытании) может принимать только два значения: х1 = 0, (событие А не наступило) с вероятностью q = 1 – p, и х2 = 1, (событие А наступило) с вероятностью p, Запишем закон распределения Х в виде таблицы M(X) = 0∙q + 1∙p = p, μ = p; M(X2) = 02∙q + 12∙p = p, D(X) = M(X2) - μ2 = p – p2 = p(1 – p) = pq. II. Теорема. Математическое ожидание и дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность появления события А постоянна и равна p есть M(X) = np, D(X) = npq. ▼ Случайная величина Х (общее число появлений события А в n испытаниях) равна сумме появлений события в отдельных испытаниях: Х = X1+ X2 +…+ Xn. Величины X1, X2,…, Xn взаимно независимые и имеют одинаковые распределения, т.е. М(X1) = М(X2) =…= М(Xn) = p D(X1) = D(X2) =…= D(Xn) = pq, тогда М(Х) = М(X1) + М(X2) +…+ М(Xn) = np, D(Х) = D(X1) + D(X2) +…+ D(Xn) = npq, Пример. Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти математическое ожидание и дисперсию случайной величины Х (число появлений события в этих испытаниях). ▼ n = 10. p = 0,6; q = 0,4. M(X) = np = 10∙0,6 = 6, т.е. в 10 испытаниях событие появится в среднем в 6 случаях, D(X) = npq = 10∙0,6∙0,4 = 2,4. Следствие. Математическое ожидание и дисперсия частости m/n появления события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна
▼ Случайная величина Х = m – общее число появления события А в n независимых испытаниях. Вычислим математическое ожидание и дисперсию частости:
Пример. Вероятность выигрыша по облигации за все время его действия равна 0,1. Найти математическое ожидание, дисперсию и стандартное отклонение доли (частости) выигравших облигаций среди 19 приобретенных. ▼ n = 19. p = 0,1; q = 0,9.
Основные законы распределения ДСВ.
Биномиальное распределение. Дискретная случайная величина Х, которая принимает значение m с вероятностью Теорема. Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, есть: M(X) = np, D(X) = npq. Пример. Вероятность попадания стрелком в мишень равна 0,8. Записать закон распределения случайной величины Х (числа попаданий в мишень), если стрелок сделал 20 выстрелов. Найти М(Х), D(X). ▼ n = 20. p = 0,8; q = 0,2. P(X = m) = М(Х) = np= 20∙0,8 = 16 – среднее число попаданий в мишень при 20 выстрелах, D(X) = npq = 20∙0,8∙0,2 = 3,2.
Закон распределения Пуассона. Дискретная случайная величина Х, которая принимает значение m с вероятностью Теорема. Математическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е. M(X) = λ, D(X) = λ. Пример. Случайная величина Х распределена по закону Пуассона с параметром λ =2. Найти вероятности Р(Х = 0), Р(Х > 0). ▼ m = 0, P(X = 0) = e 1 – 0,1353 = 0,8675.
Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р, и, следовательно, вероятность его непоявления q = 1 – p. Испытания заканчиваются, как только появится событие А. Таким образом, если событие А появилось в m – ом испытании, то в предшествующих m – 1 испытаниях оно не появилось. Пусть в первые m – 1 испытаниях событие А не наступило, а в m – ом испытании появилось, т.е.
Вероятность такой цепочки по теореме умножения вероятности независимых событий есть Дискретная случайная величина Х, которая принимает значение m с вероятностью
называется геометрическим распределением с параметром р. Теорема. Математическое ожидание и дисперсия случайной величины Х, имеющей геометрическое распределение с параметром р, равна M(X) = 1/p, D(X) = q/p2, где q = 1 – p. Пример. Из большой партии изделий контроль качества проводится до 1 – го появления бракованного изделия. В результате проверок обнаружилось, что бракованное изделие впервые появляется в среднем при десятом испытании.. Определить вероятность р брака изделия. ▼ Случайная величина Х – число испытаний до 1 – го появления бракованного изделия. По условию, среднее значение М(Х) = 10. Из выражения M(X) = 1/p = 10 следует, что р = 1/10 = 0,1.
36 38 37 41 37 41 38 42 39 40 38 42 39 42 39 40 40 39 40 39 Исходные данные из n = 20 наблюдений представляют собой несгруппированные данные. Произведем группировку исходных данных. Группировка состоит в объединении данных с одинаковыми или близкими значениями признака в группы и подсчете частоты каждой группы. Для осуществления группировки ранжируем исходные данные, т.е. расположим их в возрастающем порядке. В результате получим следующий ранжированный ряд: 36 37 37 38 38 38 39 39 39 39 39 40 40 40 40 41 41 42 42 42. Некоторые данные принимают одни и те же значения, причем одни значения встречаются чаще, другие реже.
Вариантами xi называются различные значения признака, встречающие в совокупности. Частотой варианты xi называется число mi, показывающее, сколько раз эта варианта встречается в совокупности., причем Σ mi = n. Частостью (относительной частотой, долей) варианты называется отношение частоты варианты к объему совокупности, т.е.
В рассматриваемом примере: - варианты xi: 36 37 38 39 40 41 42; - частоты mi: 1 2 3 5 4 2 3; - частости w i: 0,05 0,10 0,15 0,25 0,20 0,10 0,15. Вариационным рядом называется ранжированный в порядке возрастания ряд вариантов с соответствующими им весами (частотами или частостями). Вариационный ряд называется дискретным, если его варианты принимают конкретные изолированные значения, и – интервальным, если его варианты принимают любые значения из некоторого числового промежутка. Общий вид дискретного вариационного ряда
Таким образом, дискретный вариационный ряд состоит из двух элементов: варианты и частоты (частости). При изучении вариационных рядов используются также понятие накопленной частоты. Накопленная частота Накопленные частоты (частости) для каждого интервала находятся последовательным суммированием частот (частостей) всех предшествующих интервалов, включая данный, т.е
Представим сгруппированные данные рассматриваемого примера в виде таблицы
Эмпирической функцией распределения Fn(x) называется частость того, что признак (случайная величина Х) примет значение, меньше заданного х, т.е. Fn(x) = w(X < x) = Для дискретного вариационного ряда эмпирическая функция распределения представляет собой разрывную ступенчатую функцию. Для рассматриваемого примера
Для графического изображения дискретного вариационного ряда используется полигон частот (частостей) и кумулятивная кривая. Полигоном частот ( частостей) называют ломанную, отрезки которой соединяют точки (xi, mi), или (xi, wi), i = 1,2,… Кумулятивная кривая (кумулята) – кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломанную, соединяющую точки (xi, На рис. представлены графики полигона частот и кумуляты для рассматриваемого примера.
Интервальный ряд. При построении интервального ряда произведем следующую группировку данных. Весь диапазон изменения признака в совокупности разбивают на равные интервалы шириной Δх, равной
где xmin, xmax – наименьшее и наибольшее значение признака в совокупности, а к – число интервалов. Число интервалов следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака. Рекомендуемое число интервалов определяется по формуле: k = 1 + 3,322lgn. Если окажется, что Δх - дробное число, то за длину интервала берут либо ближайшее целое число, либо ближайшую простую дробь.
За начало первого интервала рекомендуется брать величину xнач = xmin – Δх/2. Конец последнего интервала должен удовлетворять условию xкон – Δх ≤ xmax < xкон. Промежуточные интервалы получают, прибавляя к концу предыдущего интервала величину Δх. Объединяют данные, попавшие в соответствующие интервалы группировки. Если значение признака находится на границе интервала, то его присоединяют к правому интервалу. Частотой интервала называется число данных, попавших в соответствующий интервал. Частота интервала относится ко всему интервалу группировки. Иногда интервальный вариационный ряд условно заменяют дискретным, В этом случае серединное значение i – го интервала принимают за вариант xi, а соответствующую интервальную частоту mi – за частоту этого варианта.. Пример 2. Массив данных представлен следующим ранжированным рядом 10 12 14 16 17 18 19 21 22 24 24 25 25 26 26 27 27 28 29 29 31 32 32 33 33 34 34 35 36 37 38 39 39 40 41 42 43 44 45 47 Случайная величина Х приняла n = 40 значений, причем xmin = 10, xmax = 47. Произведем группировку исходных данных.
Для графического изображения интервального вариационного ряда используются гистограмма и кумулятивная кривая. Гистограмма имеет ступенчатой фигуры из прямоугольников с основаниями, равными ширине интервала Δх и высотами, равными частоте mi соответствующего интервала. При построении кумуляты интервального ряда по оси абсцисс откладываются интервалы ряда, а по оси ординат – накопленные частости. При этом необходимо помнить, что накопленная частость интервала группировки относится к верхней границе интервала. График эмпирической функции распределения Fn(x) интервального вариационного ряда совпадает с кумулятой. На рис. представлены графики гистограммы и кумуляты
Вариационный ряд является статистическим аналогом (реализации) распределения признака (случайной величины Х). В этом смысле полигон (гистограмма) аналогичен кривой распределения f(x), а эмпирическая функция распределения – функции распределения F(x) случайной величины Х.
Числовые характеристики вариационного ряда.
Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие им частоты, деленная на cуvму частот, т.е.
где xi – варианты дискретного ряда или середины интервалов интервального ряда, mi – соответствующие им частоты, n – объем ряда. Среднее арифметическое вариационного ряда характеризует значение признака, вокруг которого концентрируются наблюдения. Дисперсией σ2 вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической, т.е.
Дисперсия вариационного ряда определяет меру рассеяния признака в совокупности относительно средней арифметической. Формулу для расчета дисперсии можно преобразовать к виду
Средним квадратическим отклонением называется корень квадратный из дисперсии, т.е.
Среднее квадратическое отклонение показывает, насколько в среднем отклоняется случайная величина в совокупности относительно средней арифметической. Пример. Вычислить ▼ Исходные данные и расчетные показатели представим в виде расчетной таблицы.
Окончательно имеем
Пример. Вычислить ▼ Исходные данные и расчетные показатели представим в виде расчетной таблицы.
Окончательно имеем
Точечные оценки. Точечной оценкой q параметра q0 называется числовое значение этого параметра, полученное по выборке, т.е. q0 ≈ q . Для того чтобы выборочная оценка давала хорошее приближение оцениваемого параметра, она должна удовлетворять определенным требованиям (несмещенности, эффективности и состоятельности). 1. Несмещенность оценок. Оценка q является несмещенной, если её математическое ожидание равно оцениваемому параметру q0 при любом объеме выборки, т.е. M(q) = q0. Если это не так, то оценка называется смещенной. Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании. Выборочная средняя Выборочная дисперсия σ2 является смещенной оценкой генеральной дисперсии В качестве несмещенной оценки генеральной дисперсии используется величина (исправленная дисперсия):
2. Эффективность оценок. Несмещенная оценка q называется эффективной, если она имеет минимальную дисперсию по сравнению с другими выборочными оценками, т.е. minσ2(q). Выборочная средняя 3. Состоятельность оценок. Оценка q называется состоятельной, если при
Иначе говоря, состоятельной называется такая оценка, которая дает точное значение для большой выборки независимо от входящих в нее конкретных наблюдений. Выборочная средняя Теорема. Выборочные В теории вероятности было показано, что Величины Если при определении Сведем рассмотренные формулы в таблицу.
Точечная оценка параметров Пример. Выборочно обследовали партию кирпича, поступивших на стройку. Из 100 проб в 12 случаях кирпич оказался бракованным. Найти оценку w доли бракованного кирпича и среднюю ошибку выборки σw. ▼ По условию n = 100, m = 12, тогда
Пример. Из партии деталей отобрано 200, распределение которых по размеру задано в таблице. Найти выборочную среднюю ▼ Исходные данные и расчетные показатели представим в расчетной таблице
Окончательно имеем
Интервальные оценки. Пусть выборочная характеристика q служит оценкой неизвестного параметра q0. Наряду с точечными оценками параметров (в виде одного числа) рассматривают интервальные оценки (в виде двух чисел – концов интервала). Интервальной называют оценку, определяющую числовой интервал (q – Δ; q + Δ), Δ > 0, содержащий оцениваемый параметр q0, т.е. q – Δ < q0 < q + Δ, или | q - q0 | < Δ. Доверительным интервалом называется интервал | q - q0 | < Δ, в котором с заданной вероятностью g заключен неизвестный параметр q0, а сама вероятность g называется доверительной вероятностью, т.е. P (| q - q0 | < Δ) = g Доверительный интервал (q – Δ; q + Δ) покрывает неизвестный параметр q0 с заданной вероятностью g. Величина Δ в статистике называется предельной ошибкой выборки и показывает наибольшее отклонение выборочной средней (доли) от генеральной средней (доли), которая возможна с заданной вероятностью g. Уровнем значимости a называется вероятность P (| q - q0 | ≥ Δ) = a, причем a = 1 - g. Критерий согласия Пирсона. Критерий согласия – это критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Пусть требуется проверить гипотезу, что случайная величина Х распределена по нормальному закону, т.е. Х ~ N( На основании выборки x1, x2,…,xn объема n эту гипотезу надо принять или опровергнуть при заданном уровне значимости. Разобьем весь интервал наблюдаемых значений Х на к – равных интервалов, а в качестве эмпирической частоты mi принимаем число значений случайной величины Х, попавших в i –ый интервал. В результате получим следующий ряд распределения
Вычисляем выборочные среднюю Неизвестные параметры (
Поскольку объем выборочной совокупности равен n, то теоретическая частота соответствующего интервала определяется как В качестве критерия проверки нулевой гипотезы принимается случайная величина
где Наблюдаемое значение критерия Если Пример. По данным распределения объема товарооборота магазинов района проверить гипотезу о нормальности распределения. ▼ Случайная величина Х – объемы товарооборота магазинов. Исходные данные и расчетные показатели представим в расчетной таблице.
Окончательно имеем
Полагаем
причем полагают α1 = - ∞, βк = ∞. Результаты расчета представим в таблице
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.90.44 (0.155 с.) |
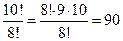 .
.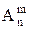 и определяется выражением:
и определяется выражением: 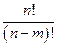 .
.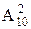 = 90.
= 90.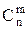 и определяется выражением:
и определяется выражением: 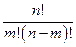 .
.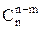 , в частности
, в частности 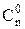 =
= 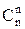 = 1,
= 1, 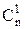 = n.
= n.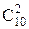 = 45.
= 45.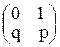 , тогда
, тогда .
. ,
,  .
. .
.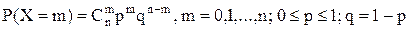 , называется распределенной по биномиальному закону с параметрами n, p.
, называется распределенной по биномиальному закону с параметрами n, p. - закон распределения Х,
- закон распределения Х, , называется распределенной по закону Пуассона с параметром λ
, называется распределенной по закону Пуассона с параметром λ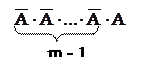

 , причем Σw i = 1.
, причем Σw i = 1. показывает, сколько наблюдалось вариантов со значением признака Х < х. Отношение накопленной частоты
показывает, сколько наблюдалось вариантов со значением признака Х < х. Отношение накопленной частоты  .
. .
.
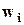
 .
.


 ,
, . Примем Δх = 6. За начало первого интервала возьмем xнач = 10 – 3 = 7, тогда получим следующие интервалы: [7; 13), [13; 19),…, [43; 49). Подсчитываем число данных, попавших в каждый интервал группировки (частоту). Результаты группировки представим в таблице
. Примем Δх = 6. За начало первого интервала возьмем xнач = 10 – 3 = 7, тогда получим следующие интервалы: [7; 13), [13; 19),…, [43; 49). Подсчитываем число данных, попавших в каждый интервал группировки (частоту). Результаты группировки представим в таблице

 ,
, .
. , где
, где  .
. .
. по данным примера 1.
по данным примера 1.


 ;
; 
 ,
,  .
.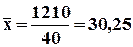 ;
; 
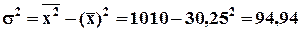 ,
,  .
. является несмещенной оценкой генеральной средней
является несмещенной оценкой генеральной средней  , т.е. M(
, т.е. M(
 , т.е. M(σ2) ≠
, т.е. M(σ2) ≠  , для которой
, для которой  .
.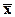 является эффективной оценкой генеральной средней
является эффективной оценкой генеральной средней  она стремится по вероятности к оцениваемому параметру q0, т.е.
она стремится по вероятности к оцениваемому параметру q0, т.е.
 ,
,  .
. ,
,  называются средними ошибками выборки.
называются средними ошибками выборки.



 ;
;  .
. ;
; 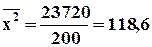
 ,
,  .
. ).
).





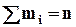



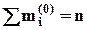
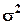 .
. .
. .
. ,
, - эмпирические и теоретические частоты в i –ом интервале; к – число интервалов. Этот критерий согласия был предложен Пирсоном.
- эмпирические и теоретические частоты в i –ом интервале; к – число интервалов. Этот критерий согласия был предложен Пирсоном. сравнивается с критическим
сравнивается с критическим  , определяемое по таблице при заданном уровне значимости α и числу степеней свободы ν = k – r – 1, где r – число параметров распределения, к – число интервалов.
, определяемое по таблице при заданном уровне значимости α и числу степеней свободы ν = k – r – 1, где r – число параметров распределения, к – число интервалов. , тогипотеза о нормальности принимается, если
, тогипотеза о нормальности принимается, если  ;
; 
 ,
,  .
.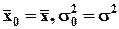 . Теоретические частоты
. Теоретические частоты  в i –ом интервале определяются из выражения:
в i –ом интервале определяются из выражения: 


