
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полигон частот. Выборочная функция распределения и гистограмма
Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x 1, n 1), (x 2, n 2),…, (xk, nk), где xi откладываются на оси абсцисс, а ni – на оси ординат. Если на оси ординат откладывать не абсолютные (ni), а относительные (wi) частоты, то получим полигон относительных частот (рис.1). В теории вероятностей для характеристики распределения случайной величины
равная вероятности события Одной из основных характеристик выборки является выборочная (эмпирическая) функция распределения
где Из определения имеем следующие свойства функции 1. 2. 3.
Напоминаем, что такими же свойствами обладает и функция распределения Функция Аналитически
где Замечание. В случае интервального вариационного ряда под Перед вычислением Пример. Построить выборочную функцию распределения по наблюдаемым данным, приведенным в примере 2.1. Решение. Используя соответствующий этим данным дискретный вариационный ряд (см. табл. 2.1), вычислим значения Таблица 2.3
Из графика Напомним, что
Рис. 2.1. График выборочной функции распределения (пример 2.4) По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x. Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной ni /h (гистограмма частот) или wi /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице. В качестве оценки плотности распределения вероятности непрерывной случайной величины используют гистограмму относительных частот. График плотности распределения генеральной совокупности Напомним свойства функции плотности вероятности: 1. р (х) ≥ 0; 2. площадь под графиком р (х) равна единице:
3. Р (Х Первые два свойства выполняются и для гистограммы, третье свойство, естественно, выполняется лишь асимптотически.
¨Пример 2.5. Построим гистограмму относительных частот выборочной совокупности из примера 2.3. Решение. Используя интервальный вариационный ряд (см. табл. 2.2), находим высоты
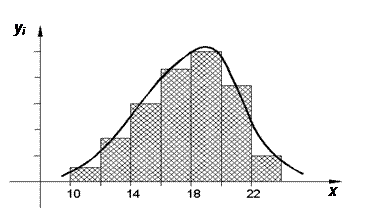
Рис. 2. График гистограммы Пример. Выборочно обследовано 26 предприятий лёгкой промышленности по валовой продукции. Получены следующие результаты в млн. руб.: 15,0; 16,4; 17,8; 18,0; 18,4; 19,2; 19,8; 20,2; 20,6; 20,6; 20,6; 21,3; 21,4; 21,7; 22,0; 22,2; 22,3; 22,7; 23,0; 24,2; 24,2; 25,1; 25,3; 26,0; 26,5; 27,1. Составить интервальное распределение выборки с началом х1=15 и длинами частичных интервалов h=2,5. Построить гистограмму частот.
Для составления интервального распределения составим таблицу. В первой строке расположим в порядке возрастания интервалы, длина каждого из которых h=2,5. Во второй строке запишем количество значений признака в выборке, попавших в этот интервал (т.е. сумму частот вариант, попавших в соответствующий интервал). Интервальный статистический ряд таков:
Объем выборки n=2+5+10+4+5=26. Для построения гистограммы частот на оси абсцисс откладываем частичные интервалы; на каждом из них строим прямоугольники высотой
15 17,5 20 22,5 25 27,5
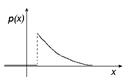
Площадь каждого прямоугольника равна частоте интервала, на котором он построен. Сумма площадей этих прямоугольников равна объёму выборки. ◄ Для того чтобы увеличить точность приближения необходимо обеспечить значительное увеличение количества наблюдений (объем выборки Анализируя гистограмму, можно сделать вывод о виде и свойствах исследуемой генеральной совокупности Х. Укажем три наиболее часто используемых на практике вида распределения случайных величин. Схематические графики их функций плотности вероятности имеют следующий вид:
В случае нормально распределенных случайных величин под пиком гистограммы располагается значение, равное генеральному среднему (или математическому ожиданию)
Вопросы для самопроверки
1. Что понимается под генеральной совокупностью? 2. Что такое выборка, размах выборки, объем выборки? Как обеспечивается представительность ее? 3. Объясните, как получают повторную и бесповторную выборки? 4. Что называют ошибкой репрезентативности? 5. Что такое частота появления варианты в выборке? 6. Как получают относительную частоту варианты в выборке? 7. Объясните, как получают вариационный ряд, статистический ряд распределения. 8. Что мы называем функцией распределения и статистической функцией распределения? Какими свойствами обладает статистическая функция распределения? 9. Дайте определение группированного статистического ряда. Как строится гистограмма? 10. Что такое гамма-функция? 11. Запишите формулы плотности распределения для нормального, 12. Как выполняется чертеж многоугольника распределения относительных частот? 13. Как выполняется чертеж гистограммы распределения плотности относительных частот?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.70.191 (0.034 с.) |
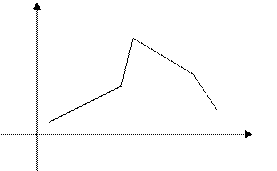 Рис. 1.
Рис. 1.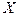 служит функция распределения
служит функция распределения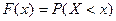 ,
,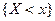 , где
, где 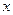 – любое действительное число.
– любое действительное число. ,
,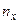 – количество элементов выборки, меньших чем
– количество элементов выборки, меньших чем 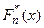 есть относительная частота появления события
есть относительная частота появления события 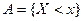 в
в 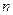 независимых испытаниях. Главное различие между
независимых испытаниях. Главное различие между  и
и 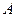 , а выборочная функция распределения
, а выборочная функция распределения 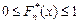 .
.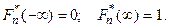
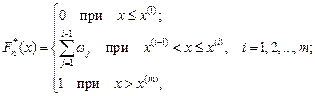
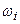 – соответствующие относительные частоты;
– соответствующие относительные частоты; 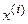 – элементы вариационного ряда (варианты).
– элементы вариационного ряда (варианты).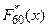
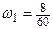
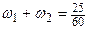
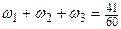
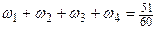
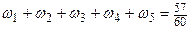

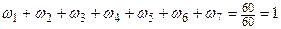
 объема
объема 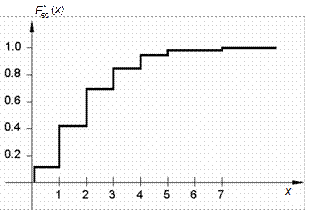
 .
. ;
;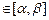 ) =
) = 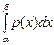 .
.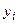 по формуле
по формуле 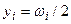 . График построенной гистограммы приведен на рис. 2.2. Здесь же штриховой линией отмечен предполагаемый график неизвестной плотности
. График построенной гистограммы приведен на рис. 2.2. Здесь же штриховой линией отмечен предполагаемый график неизвестной плотности 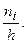
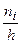


 10/2,5
10/2,5






 5/2,5
5/2,5







 хi – xi+1
хi – xi+1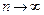 ) при одновременном уменьшении шага разбиения диапазона выборки
) при одновременном уменьшении шага разбиения диапазона выборки  . В этом случае мы можем сколь угодно точно приблизить ступенчатую гистограмму к теоретической кривой функции плотности вероятности.
. В этом случае мы можем сколь угодно точно приблизить ступенчатую гистограмму к теоретической кривой функции плотности вероятности.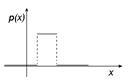
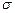 )
)
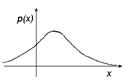
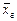 = М (Х). Наиболее часто реализуемые значения генеральной совокупности лежат в окрестности этого значения. Значения под убывающими ветвями практически не реализуются, их влиянием, в среднем, можно пренебречь.
= М (Х). Наиболее часто реализуемые значения генеральной совокупности лежат в окрестности этого значения. Значения под убывающими ветвями практически не реализуются, их влиянием, в среднем, можно пренебречь.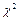 и распределения Стьюдента.
и распределения Стьюдента.


