
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метамодели объектов теории массового обслуживания
Метамодели объектов теории массового обслуживания предназначены для исследования объектов по обслуживанию заявок, поступающих в систему массового обслуживания (СМО) нерегулярно. СМО состоит из ресурсов (аппараты обслуживания) и транзактов (заявки на обслуживание). Примерами СМО могут служить цеха или производственные участки, где аппараты – рабочие места и единицы оборудования, заявки – отдельные детали или партии. Также в качестве СМО могут быть представлены отдельные виды оборудования, например теплообменники, где ресурсы – это различные области теплообменников, а заявки – отдельные порции теплообменивающихся сред. Модели СМО должны описывать процессы прохождения заявок через СМО. Состояние СМО выражается совокупностью переменных, имеющих преимущественно дискретный характер. Например, состояние аппарата характеризуется дискретной переменной V, которая может иметь значения 1 – аппарат свободен или 0 – аппарат занят. К другим переменным относятся длина очереди, тип очереди и т.д. Результат анализа выражается при помощи следующих характеристик: производительность СМО; среднее и максимальное время обслуживания заявок; средняя длина очереди; коэффициенты загрузки аппаратов; вероятность обслуживания заявок за заданное время. ММ СМО могут быть аналитическими (совокупности явных зависимостей выходных параметров от внутренних и внешних) и имитационными (алгоритмы, описывающие изменения переменных состояния при моделировании с использованием генератора случайных чисел, накоплением и обработкой статистики).
4.3. Моделирование на мета уровне на примере расчета устойчивости системы автоматического управления теплообменника
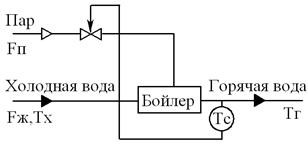
В системах теплоснабжения используются теплообменники, которые представляют собой пароводяные бойлерные установки, предназначенные для передачи тепла от пара к воде и поддержания необходимой температуры горячей воды. Поддерживать постоянную температуру воды можно путем изменения расхода пара, подаваемого в бойлер. Для этого на паропроводе устанавливают регулирующий клапан, а на трубопроводе нагреваемой воды – датчик терморегулятор, который воздействуют на исполнительный механизм регулирующего клапана (рис. 17а).
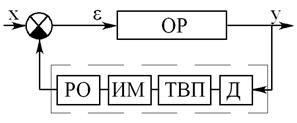
а) б) Рис. 17. Функциональная схема и схема регулирования бойлерной установки В пароводяной бойлерной установке вода нагревается насыщенным водяным паром (расход При температуре воды, выходящей из бойлера выше 60 Бойлерная установка, в которой производится регулирование, является объектом регулирования (ОР). Регулятор состоит из датчика (Д) температуры, сопротивления типового вторичного прибора (ТВП), служащего для преобразования и усиления сигнала датчика, исполнительного механизма-гидравлического поршневого устройства (ИМ) и регулирующего органа-клапана (РО). Элемент сравнения, конструктивно входящий в регулятор, описывается алгебраическим уравнением
где Если в элементе сравнения сигналы х и y равны, то это означает, что расход пара бойлерной установки не изменяется, если же сигналы х и y не равны, то расход пара изменяется. Согласно схеме регулирования (рис. 17б), в рассматриваемой системе можно выделить следующие элементы с передаточными функциями: 1) объект регулирования – бойлерная установка (ОР)
2) чувствительный элемент – термометр сопротивления (Д)
3) типовой вторичный прибор (ТВП)
4) гидравлический исполнительный механизм
5) регулируемый клапан
Передаточная функция замкнутой системы регулирования температуры бойлерной установки имеет вид
где Передающая функция бойлерной установки (77) получена при следующих допущениях: бойлер обладает сосредоточенными параметрами, т.е. температура воды в бойлере
Характеристические полиномы и уравнения являются исходным материалом для исследования систем на устойчивость. Наиболее предпочтительным с учетом использования ЭВМ является метод Рауса [3], который состоит в следующем: Пусть задано характеристическое уравнение системы
Составляется таблица Рауса
Для любого из коэффициентов таблицы Рауса
Причем коэффициентам характеристического полинома Для того, чтобы система была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительны, т.е. Если это условие не выполняется то еще одним необходимым условием устойчивости является положительность всех коэффициентов полинома, т.е.
4.4. Общая схема преобразования ММ
Рассмотренные выше ММ различных уровней могут быть исследованы (преобразованы) при помощи различных методов [2,8-10], выбор которых зависит от вида получаемых систем уравнений. Общая схема преобразования моделей отражена при помощи графа (рис. 18) [6].
Рис. 18. Общая схема преобразования ММ
Вершины – это ММ. Ветви – методы. Ветви 1, 8, 10, 11 отражают постановку задачи, т.е. переход от физического процесса к его математическому описанию в виде системы уравнений. Ветви 2, 3, 4, 9 объединяют методы, предназначенные для решения дифференциальных уравнений и их систем. Ветвь 2 – для решения стационарных задач, где в силу
Ветви 5, 6, 7 – для решения систем, в том числе нелинейных алгебраических уравнений. Ветвь 5 – прямое решение САУ итерационными методами, например метод простой итерации, метод Зейделя. Ветвь 6 предполагает предварительную линеаризацию задачи, т.е. получение из САУ СЛАУ, например метод Ньютона (см. лаб. раб. №6 [10])). Ветвь 7 – методы для решения СЛАУ, к которым относятся аналитические методы Гаусса, Гаусса–Джордана, формулы Крамера, а также итерационные методы простой итерации, метод Зейделя (см. лаб. раб. №5 [10])). К методам ветви 12 относятся, например, методы статистического анализа (см. лаб. раб. №7[10])).
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.184 (0.016 с.) |
 ) до температуры
) до температуры  . Расход воды, проходящей через бойлерную установку, равен
. Расход воды, проходящей через бойлерную установку, равен 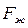 , его температура на воде составляет
, его температура на воде составляет  , а удельная теплоемкость
, а удельная теплоемкость  .
. С, терморегулятор воздействует на исполнительный механизм регулирующего клапана, который постепенно закрывается, уменьшая подачу пара в бойлер, при понижении температуры воды клапан открывается. Функциональная схема регулирования температуры бойлерной установки представлена на рис. 17б.
С, терморегулятор воздействует на исполнительный механизм регулирующего клапана, который постепенно закрывается, уменьшая подачу пара в бойлер, при понижении температуры воды клапан открывается. Функциональная схема регулирования температуры бойлерной установки представлена на рис. 17б. ,
, – ошибка системы, х – сигнал, устанавливающий заданное значение температуры воды, y – фактическое значение температуры воды.
– ошибка системы, х – сигнал, устанавливающий заданное значение температуры воды, y – фактическое значение температуры воды.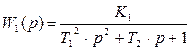 ; (72)
; (72)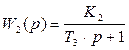 ; (73)
; (73) ; (74)
; (74)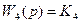 ; (75)
; (75) . (76)
. (76)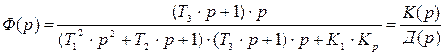 , (77)
, (77) – коэффициент усиления регулятора
– коэффициент усиления регулятора 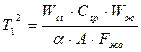 ;
; 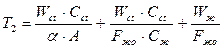 ;
;  ;
; 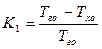 ;
; 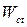 – масса теплопередающих стенок;
– масса теплопередающих стенок;  – суммарная поверхность стенок м2.
– суммарная поверхность стенок м2. постоянна во всех точках объема; температура теплопередающих стенок
постоянна во всех точках объема; температура теплопередающих стенок  одинакова во всех точках, их термическое сопротивление пренебрежимо мало; коэффициент теплоотдачи между жидкостью и поверхностью металлических стенок, а также удельные теплоёмкости воды
одинакова во всех точках, их термическое сопротивление пренебрежимо мало; коэффициент теплоотдачи между жидкостью и поверхностью металлических стенок, а также удельные теплоёмкости воды 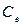 и материала стенок
и материала стенок  постоянны во времени; насыщенный водяной пар при прохождении через бойлер полностью конденсируется, отдаёт тепло фазового перехода и выводится в виде конденсата при той же температуре; тепло, выделяющееся при конденсации пара, расходуется на изменение температуры теплопередающих стенок и нагревание воды. Знаменатель
постоянны во времени; насыщенный водяной пар при прохождении через бойлер полностью конденсируется, отдаёт тепло фазового перехода и выводится в виде конденсата при той же температуре; тепло, выделяющееся при конденсации пара, расходуется на изменение температуры теплопередающих стенок и нагревание воды. Знаменатель 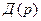 передаточной функции (77) характеризует внутренние динамические свойства системы регулирования и отражает её поведение в свободном состоянии. Полином знаменателя
передаточной функции (77) характеризует внутренние динамические свойства системы регулирования и отражает её поведение в свободном состоянии. Полином знаменателя 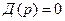 .
.

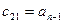


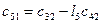



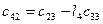
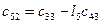




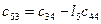

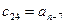


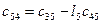


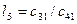
 (
( ) можно записать
) можно записать , где
, где 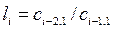 .
. с отрицательными индексами (таких коэффициентов может появиться три -
с отрицательными индексами (таких коэффициентов может появиться три -  ,
, 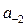 ,
,  при четной степени полинома) соответствуют нулевые значения.
при четной степени полинома) соответствуют нулевые значения. ,
,  ,
, 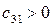 ,
,  .
. , i=0,1,…,n (тогда коэффициентам характеристического полинома с отрицательными индексами будет присваиваться не нулевое значение а малое положительное, например 10-10).
, i=0,1,…,n (тогда коэффициентам характеристического полинома с отрицательными индексами будет присваиваться не нулевое значение а малое положительное, например 10-10).
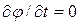 при дискретизации задачи по пространственным координатам x, y, z сразу происходит переход к системе алгебраических уравнений (САУ). Ветвь 3 – для решения нестационарных задач, где в силу
при дискретизации задачи по пространственным координатам x, y, z сразу происходит переход к системе алгебраических уравнений (САУ). Ветвь 3 – для решения нестационарных задач, где в силу  при дискретизации задачи по пространственным координатам x, y, z происходит переход к ОДУ. Для ветвей 2, 3 примерами являются методы МКР и МКЭ. Ветвь 4 – для решения нелинейных ОДУ с переходом к системам нелинейных алгебраических уравнений. Ветвь 9 – для решения линейных ОДУ с переходом к системам линейных алгебраических уравнений (СЛАУ). Для ветвей 4, 9 примерами могут служить методы Эйлера, Рунге–Кутты, многошаговые и т.д. (см. лаб. раб. №1–4 [10])
при дискретизации задачи по пространственным координатам x, y, z происходит переход к ОДУ. Для ветвей 2, 3 примерами являются методы МКР и МКЭ. Ветвь 4 – для решения нелинейных ОДУ с переходом к системам нелинейных алгебраических уравнений. Ветвь 9 – для решения линейных ОДУ с переходом к системам линейных алгебраических уравнений (СЛАУ). Для ветвей 4, 9 примерами могут служить методы Эйлера, Рунге–Кутты, многошаговые и т.д. (см. лаб. раб. №1–4 [10])


