
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулировка третьей теоремы, отвечающая реальным задачам
Положение № 1. Создание модели возможно, если критерии подобия, составленные из величин, характеризующих только ее системные параметры, равны соответствующим критериям изучаемой системы - оригинала. Примечание № 1.1. Частным случаем является равенство материальных параметров систем элементов модели и оригинала, выраженных в относительных единицах. Положение № 2. В созданной, согласно положению № 1, модели осуществление процессов, подобных оригиналу, возможно, если критерии подобия, содержащие только параметры процессов, входящих в условия однозначности и в том числе начальные условия (параметры исходного режима, возмущений и отклонений), в модели и оригинале соответственно одинаковы. Примечание № 2.1. Частным случаем является равенство параметров исходного режима в модели и оригинале, выраженных в относительных единицах. Положение №3. Осуществление модели согласно формулировкам № 1 и № 2 возможно в сколь угодно сложных анизотропных (изотропные системы - одинаковые физические свойства (электропроводность, теплопроводность, упругость и т.п.) по всем направлениям внутри системы; анизотропные - имеют различные свойства по разным направлениям), нелинейных или имеющих вероятностно заданные параметры системах при условии одновременного соблюдения соответствующих дополнительных положений. Примечание № 3.1. Третья теорема в первой формулировке имеет ряд ограничивающих условий. (В частности не распространяется на автомодельные системы, для которых нельзя составить ни одного критерия, содержащего только параметры системы, но можно при любых их значениях осуществлять переход от характеристик одного процесса к характеристикам другого за счет изменения только масштабов параметров процесса). Примечание № 3.2. В указанных выше положениях понимается, что система представляет собой совокупность взаимодействующих элементов, связанных в той или иной мере единством происходящих процессов. Этих положений достаточно, чтобы пользоваться третьей теоремой, не заботясь о ее доказательствах.
Автомодельность Автомодельность какого-либо явления означает автоматическое сохранение его подобия исходному явлению (оригиналу) независимо от абсолютных значений параметров элементов той системы, в которой данное явление протекает.
Формальный признак автомодельности выполнение условия mэ.с. £ k, где mэ.с . - число параметров элементов системы. Процессы, описываемые двучленными уравнениями, всегда автомодельны. Критерии подобия автомодельных процессов при моделировании служат не для расчета значений параметров элементов модели, а лишь для определения масштабов при любых значениях параметров элементов модели. Признак автомодельности: процессы, протекающие в системах, из параметров которых нельзя составить ни одного безразмерного комплекса, являются автомодельными. При этом в представленные в критериальной форме дифференциальные уравнения и начальные условия войдут только выраженные в относительных единицах параметры, и процессы будут подобными при любых значениях параметров системы. Пример автомодельности: Уравнение второго закона Ньютона f = Md2l/dt2. Уравнение содержит два члена (n = 2), четыре параметра (f, M, l, t), т.е. m = 4, и если оно записано в СИ, то q = 3. Согласно первой теореме подобия, число критериев подобия n - 1 = 1. Это единственный критерий p = Ml/(ft2). Так как критерий подобия один, то число m - k должно быть равно единице, следовательно, число независимых параметров k = 3. Действительно: формулы размерностей всех параметров: [f] = [M]1[L]1[T]-2; [M] = [M]1[L]0[T]0; [l] = [M]0[L]1[T]0; [t] = [M]0[L]0[T]1. Матрица размерностей:
Общее число определителей третьего порядка: C43 = 4!/[3!(4 - 3)!] = 4 ни один из них не равен нулю потому, что не ни один из них не содержит строку, являющуюся линейной комбинацией двух остальных. Следовательно, любые три из четырех параметров могут быть выбраны в качестве независимых (в том числе f и M), т.е. процессы, описываемые уравнением второго закона Ньютона, подобны при любых значениях f и M и, следовательно, автомодельны.
Пример к автомодельности: Включение R1 L1 цепи на постоянное напряжение u1. Уравнение описываемого процесса u1 = i1R1 + L1di1 / dt1. Критерии подобия процесса имеют вид (один из возможных)
причем Для обеспечения второго процесса первому (исходному) необходимо, чтобы определяющие критерии в сходственные моменты времени были равны, т.е. чтобы
При любых заданных значениях L2 и R2 всегда можно удовлетворить этим условиям, соответствующим выбором величины t2 и, следовательно, mt = t1 / t2. Если R1 / L1 ¹ R2 / L2 или mR / mL ¹ 1, то и mt = mR / mL ¹ 1. Таким образом, при соответствующем выборе масштаба времени рассматриваемые два процесса будут подобны при любых значениях параметров элементов второй системы (R2 L2). Значение еще одного параметра второй системы u2 никакого влияние на подобие процессов не оказывает, поскольку он входит в неопределяющий критерий. Следовательно, величина u2 может быть любой, что также соответствует и тому, что u2 входит в систему независимых параметров второго процесса. Итак, при любых значениях параметров элементов системы (u, R, L) процессы в цепях RL оказываются подобными. Следовательно, эти процессы можно считать автомодельными. При этом необходимо учитывать ограничения, наложенные на выбор масштаба времени mt. Процессы, протекающие в цепях RLC, не могут быть полностью автомодельными, поскольку число независимых параметров меньше числа параметров системы.
Заключительный пример к теоремам подобия: Дифференциальное уравнение переходного процесса в цепи из активного сопротивления R, индуктивности L и емкости C при включении на источник постоянного напряжения u
Для конкретного процесса следует задать значения параметров u, R, L, C и начальные условия i = 0 при t = 0. При этом по p - теореме из шести параметров (m = 6) три являются независимыми (k = 3), и, следовательно, число критериев подобия составляет m - k = 3, причем существует 15 форм записи трех критериев. Если независимые переменные u, C и t, получаются следующие критерии:
Пусть существуют два процесса, у которых критерии p2 и p3 равны. Покажем, что равенства этих критериев достаточно для подобия процессов. Если p2 и p3 соответственно одинаковы у двух процессов, то R1C1/t1 = R2C2/t2; L1C1/t12 = L2C2/t22, или
Поскольку u, C и t - независимые параметры, то и масштабы можно выбрать произвольно. Отсюда масштабы сопротивлений и индуктивностей: mR = mt/mC; mL = mt2/mC. Если произвольно выбраны mu, mC и mt и определены mR и mL, то при p2 = p3 масштаб токов mi, будет таким, что всегда справедливо условие mi mt/(mu mC) = 1. Параметры первого процесса: u1 = 500 В, R1 = 30 Ом, L1 = 2.62 Гн, C1 = 2×10-3 Ф. Зададимся mu = 5; mC = 0.4; mt = 1. Тогда mR = mL = 1/0.4 = 2.5, и параметры второго процесса u2 = u1/mu = 500/5 = 100 В; R2 = R1/mR = 30/2.5 = 12 Ом; L2 = L1/mL = 2.62/2.5 = 1.045 Гн; C2 = C1/mC = 2×10-3/0.4 = 5×10-3 Ф. При данных параметрах для сходственных моментов времени критерии p2 и p3 соответственно одинаковы для обоих процессов. Например, при t1 t2 = 0.125 c p2 = 30×2×10-3/0.125 = 12×5×10-3/0.125 = 0.480; p3 = 2.62×2×10-3/0.1252 = 1.045×5×10-3/0.1252 = 0/336. Для обоих процессов R2C - 4L < 0 и, следовательно, решение исходного уравнения имеет вид
Ниже приведены результаты расчета значений токов i1 и i2. Соответствующие зависимости i = f (t) представлены на рисунке. Видно, что для сходственных моментов времени отношения токов постоянно: mi = 2. Таблица 4
Таким образом, равенство критериев подобия p2 и p3 оказывается достаточным для того, чтобы выполнялись условия, накладываемые на масштабы. Поскольку пропорциональность всех параметров существует и эти условия соблюдены, то рассматриваемые процессы подобны.
Масштабные уравнения
Рис. 12 R-L-с цепочка
Пусть есть два процесса с параметрами: 1) {L1, R1, c1, t1, i1, U1, w1} = P1 2) {L2, R2, c2, t2, i2, U2, w2} = P2 По каждому из параметров введены определенные масштабные коэффициенты
Воспользуемся ранее выведенными критериями, но по принципу размерности. 1) 2) 3) 4) Группа независимых параметров [U, R,c]. Для 1-ой системы
Для 2-ой системы с учетом масштабов:
" pI = idem (все критерии одинаковы для подобных объектов)
Эти уравнения называются масштабными уравнениями, при этом также существуют независимые масштабы (соответствующие независимым параметрам) mU, mR, mc, они выбираются произвольно. Для данного примера имеем систему 4-го порядка с 4 неизвестными, но по p-теореме одно из этих уравнений является зависимым от других. В результате имеем систему 3-го порядка с 4-мя неизвестными. В общем случае решений такой системы может быть множество и выбрать одно единственное решение можно с помощью определенных ограничений, которые представляют собой условие однозначности.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.220.114 (0.033 с.) |

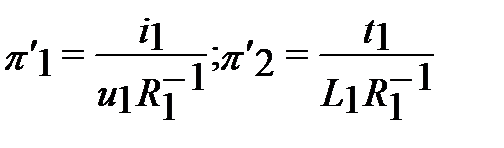
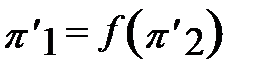 .
.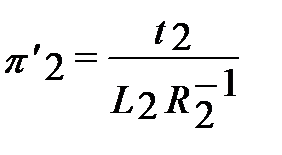 .
.

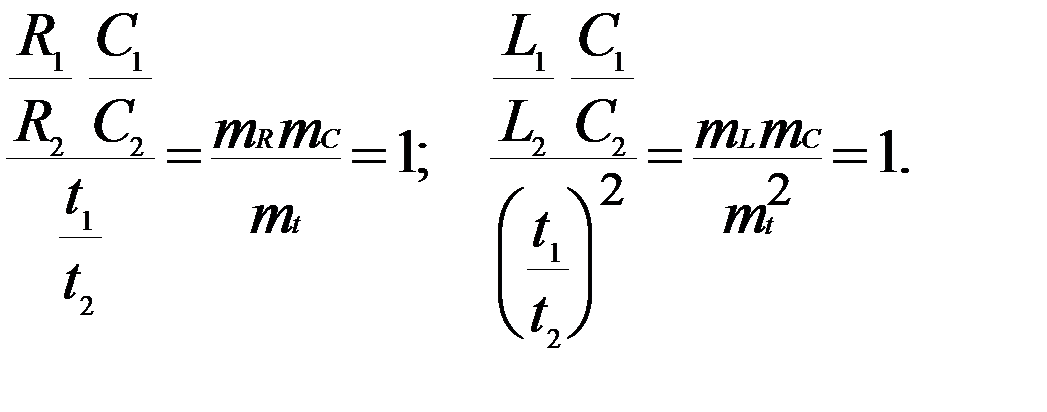



 ,
, 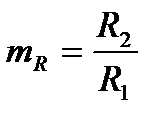 ,
, 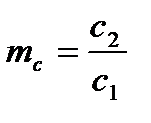 ,
, 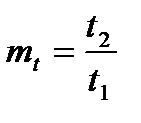 ,
,  ,
,  ,
,  .
.


 .
. ,
,  ,
,  ,
,  .
. ,
, 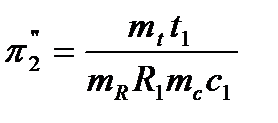 ,
,  ,
,  .
. ,
,  ,
, 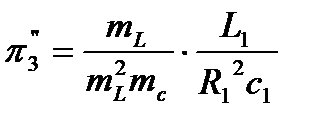 ,
,  .
.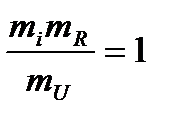 ,
,  ,
,  ,
, 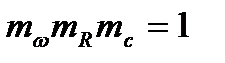 .
.


