
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Под алгебраической системой (или алгебраической структурой) в общемСтр 1 из 3Следующая ⇒
Раздел Краткое изложение раздела 1. Высшая арифметика, или теория чисел, изучает свойства натуральных чисел 1, 2, 3,... 2. Число есть абстрактная количественная мера множества элементов произвольной природы, т.е. число — это понятие, используемое для выражения количества. Число состоит из цифр. 3. Цифра — это знак для обозначения числа. 4. Знаки — это условные обозначения, предназначенные для записи математических понятий (включая понятие числа) и выкладок. 5. Позицию цифры в записи числа называют разрядом. 6. Натуральными числаминазываютсячисла, естественным образом используемые при счете. Последовательность всех натуральных чисел, расположенных в порядке их возрастания (1, 2, 3,...), называется натуральным рядом. 7. Расширенным натуральным рядом называется последовательность целых неотрицательных чисел, начинающаяся с нуля (0, 1, 2, 3...). 8. Натуральное число 9. Числа 1 и 10. Делители натурального числа 11. Простымназывается такое число 12. Составным называется такое число 13. Целое число 14. Два неотрицательные целые числа 15. Любое число, большее 1, является простым числом либо разлагается в виде произведения простых чисел одним и только одним способом. 16. Целое число - - 17. НОД совокупности целых чисел 18. НОД взаимно простых чисел 19. Под системой счисления принято понимать способы записи чисел посредством цифровых знаков (цифр) и правила действий над числами. 20. Системы счисления можно разделить на непозиционные и позиционные системы.
21. Непозиционные системы счисления характеризуются тем, что каждый знак (из совокупности знаков, принятой в данной системе для обозначения чисел) всегда обозначает одно и то же число независимо от места (позиции), занимаемого этим знаком в записи числа. 22. В позиционных системах один и тот же знак может обозначать различные числа в зависимости от места (позиции), занимаемым этим знаком в записи числа. 23. Количество различных цифр, применяемых в позиционной системе счисления (ПСС), называют ее основанием. 24. Элементарными цифрами произвольной 25. Каждая позиция числа с присвоенным ей порядковым номером называетсяразрядом числа. 26. В любой 27. Вычетом числа 28. Для перевода целого числа из одной позиционной системы в другую его надо последовательно разделить на основание 29. В настоящее время наибольшее применение находят двоично-степенные системы счисления, основаниями которых являются числа 30. Обобщением двоично-степенных систем счисления являются 31. Два целых числа 32. Вычеты положительных чисел по модулю
33. Вычеты отрицательных чисел по модулю 34. Если два числа 35. Элемент 36. Совокупность классов вычетов 37. В полной системе ненулевых вычетов по модулю 38. Отличительная особенность поразрядных операций в модульной арифметике состоит в том, что все арифметические операции (сложения, вычитания, умножения и деления) выполняются исключительно над одноразрядными числами. 39. Функция Эйлера 40. Если 41. Модульной будем называть матрицу 42. Произведением квадратных модульных матриц 43. Для произведения модульных матриц сохраняются распределительный и сочетательный законы арифметики. Вместе с тем, произведение модульных матриц, как и обычных, зависит от порядка сомножителей, т.е. умножение модульных матриц в общем случае некоммутативно. 44. Модульная матрица 45. Если определитель D модульной матрицы 46. Основание системы счисления 47. Кронекеровское произведением матриц 48. Если в кронекеровском произведении участвуют модульные матрицы
Вопросы для самопроверки 1. Приведите определение числа и цифры. 2. В чем состоит отличие числа от цифры? 3. Дайте определение математического знака. 4. Приведите определение натуральных чисел и обозначения множества натуральных чисел. 5. Чем отличается расширенный натуральный ряд от обычного натурального ряда? 6. Как обозначается делимость натурального числа без остатка?
7. Какие числа являются собственными и несобственными делителями натурального числа 8. Приведите определение простого и составного числа. 9. Как определяются общие делители совокупности натуральных чисел? 10. Какие числа называются взаимно простыми? 11. Наибольший общий делитель (НОД) совокупности натуральных чисел; определение и свойства. 12. Чему равен НОД взаимно простых чисел? 13. Приведите определение системы счисления. 14. Назовите основные классы систем счисления. 15. Дайте определение непозиционной и позиционной систем счисления. 16. Приведите примеры непозиционной и позиционной системе счисления. 17. Как определяется основание системы счисления? 18. Назовите элементарные цифры произвольной 19. Дайте определение разряда чисел в позиционной системе счисления. 20. Какой комбинацией цифр записывается основание 21. Чему равен вычет числа 22. Сформулируйте алгоритм перевода целого числа из одной позиционной системы счисления в другую. 23. В чем состоит суть циклического сдвига или круговой прокрутки кода? 24. Поясните понятие р -ично степенной системы счисления. 25. Какие два числа называют сравнимыми по модулю 26. Что означает термин класс вычетов по модулю 27. Как образуются вычеты отрицательных чисел по модулю 28. Приведите определение полной системы вычетов по модулю 29. Как определяются квадратичные вычеты и квадратичные невычеты? 30. Какова доля квадратичных вычетов и невычетов в полной системе ненулевых вычетов по модулю 31. В чем состоит особенность поразрядных операций в модульной арифметике? 32. Что представляет собой оператор XOR? 33. Приведите обозначения основных операторов модульной арифметики. 34. Составьте таблицу Кэли для операции сложения по заданному модулю. 35. Составьте таблицу Кэли для операции вычитания по заданному модулю. 36. Составьте таблицу Кэли для операции умножения по заданному модулю. 37. Составьте таблицу Кэли для операции деления по заданному модулю р. 38. Дайте определение функции Эйлера. 39. Какова особенность модульной матрицы? 40. Сформулируйте распределительный и сочетательный законы арифметики для модульных матриц. 41. Каковы условия существования обратных модульных матриц? 42. Что представляет собой кронекеровское произведение двух матриц?
43. В чем состоит особенность кронекеровского произведения модульных матриц?
Раздел Краткое изложение раздела 1. Полиномом (многочленом) называется алгебраическая сумма одночленов (мономов). 2. Моном – это произведение числа и степени формальной переменной. 3. Полная форма полинома представляет собой сумму мономов. 4. Сокращенная форма полинома образуется последовательностью коэффициентов разложения полинома, включая их нулевые значения. 5. Полином, старший коэффициент разложения которого 6. Число разрядов полинома на единицу больше его степени. 7. Степень неприводимого полинома — это максимальная степень входящего в полином монома с ненулевым коэффициентом. 8. Порядок полинома — это такое наименьшее натуральное число 9. Особенность алгебраических операций в двоичном модульном пространстве проявляется в том, что в нем операция вычитания совпадает с операцией сложения, т.е. знак 10. Простой многочлен — это такой унитарный многочлен, который нельзя разложить на произведение двух многочленов более низкой степени. 11. Приводимыми называются такие полиномы, которые могут быть представлены в виде произведения не менее двух полиномов меньшей степени. 12. Неприводимыми называются такие полиномы, которые не могут быть представлены в виде произведения двух полиномов меньшей степени. 13. Неприводимым является такой полином, который не имеет никаких других делителей, кроме тривиальных. 14. К тривиальным делителям полинома относятся единица и сам полином. 15. Неприводимый над простым полем Галуа полином называется примитивным,если его корень 16. Примитивным является такой элемент 17. Последовательность степеней, начиная с нулевой степени, примитивного элемента 18. Примитивным полиномом является неприводимый над 19. Примитивным полиномом является неприводимый над 20. Любой примитивный полином является неприводимым, тогда как не каждый неприводимый полином примитивен. 21. Двоичный полином степени
22. Двойственным неприводимым полиномомназывается полином, у которого порядок следования коэффициентов мономов является инверсным по отношению к порядку следования коэффициентов исходного полинома. 23. Полином, двойственный неприводимому, также неприводим, а двойственныйпримитивному – примитивен. 24. Двоичные полиномы первой степени являются вырожденными примитивными полиномами. 25. Последовательность степеней образующего элемента 26. Число различных элементов мультипликативной последовательности является порядком последовательности.
Вопросы для самопроверки 1. Приведите определение полинома (многочлена). 2. Что представляет собой моном многочлена? 3. Запишите пример полинома в полной и сокращенной формах. 4. Какие полиномы называются унитарными? 5. Какому условию должны удовлетворять коэффициенты полинома в модулярном пространстве? 6. Поясните схему приведения полинома к унитарной форме. 7. В чем состоит особенность выполнения операций суммирования в двоичном модульном пространстве? 8. Приведите определения приводимых и неприводимых полиномов. 9. Какие делители полиномов являются тривиальными? 10. Поясните понятие «корень полинома» и каким условиям он должен удовлетворять? 11. Поясните термин «характеристика полинома». 12. Какой элемент поля Галуа называется примитивным? 13. Дайте определение «степени» и «порядка» неприводимых полиномов. 14. Что означает термин «примитивный полином»? 15. В чем состоит физический смысл примитивности полинома? 16. Сформулируйте необходимые и достаточные условия, которым должны удовлетворять неприводимые двоичные полиномы. 17. Что такое порядок мультипликативной последовательности? 18. Приведите определение и примеры двойственного неприводимого полинома. 19. Является ли двойственный полином неприводимым (примитивным), если исходный полином неприводим (примитивен)?
Раздел Краткое изложение раздела Некоторой системе аксиом. Примером унарной (одноместной) операции может служить операция вы- числения элемента aA, обратного элементу a того же множества А. Нием элементов a и b. Щими. Как G. 21. Групповая операции чаще всего вводится посредством двух символов: (1) знака умножения или ; тогда группа называется мультипликативной и её обозначают ()G, или ()G, ; нейтральный элемент вводится симво- Ратным к a и записывают как 1 a , при этом 1aa1 или 1 aa 1; (2) знака сложения ; тогда говорят о сложении элементов из группы; группу называют аддитивной и обозначают ()G, ; нейтральный элемент Тов по модулю m. 26. Групповая операция в мультипликативной группой (G,) обозначается как умножение; число n элементов g конечной группы () G, определяет её по- Ношению () 1 n n g . 30. Элемент g, из степеней которого составлена некоторая группа ()G, , Группы. 31. Группа (G,), образуемая степенями одного примитивного элемента g, называется циклической группой и обозначается как g. 32. Существуют группы ()G, , которые порождаются не одним, а несколькими Жества S. 34. У циклической группы порядка n существует ровно ()n порождающих элементов, где — функция Эйлера. 35. Все элементы z множества p Z по модулю простого числа p обладают мультипликативно обратными значениями, причем 1 11 и 1 (p 1) (p 1) . 36. Мультипликативная группа вычетов m Z может быть образована только по модулю простого числа m p, так как если m окажется составным чис- лом, то во множестве m Z найдется хотя бы один элемент z, не являющийся Операций. F. 41. Элементами расширенного поля ()n GF p, как частный вариант, могут быть или n мерные кодовые комбинации, каждый разряд которых ir принадлежит простому полю ()GFp, то есть () i r GF p , 1,in, или поли- номы степени, не превышающей 1 n . Их обратные значения 1 a , то характеристика поля p обязана быть только Простым числом. 43. Порождающий элемент мультипликативной группы qF , обозначим его , называется также примитивным элементом поля qF. Поле qF содержит k (q 1) примитивных элементов i , 1, i k , где — функция Эйлера. Si (mod) i p, i 1,k, где i s — показатели степени, взаимно простые с Числом p. Вопросы для самопроверки Дайте определение группы. Раздел Краткое изложение раздела 1. Высшая арифметика, или теория чисел, изучает свойства натуральных чисел 1, 2, 3,... 2. Число есть абстрактная количественная мера множества элементов произвольной природы, т.е. число — это понятие, используемое для выражения количества. Число состоит из цифр. 3. Цифра — это знак для обозначения числа. 4. Знаки — это условные обозначения, предназначенные для записи математических понятий (включая понятие числа) и выкладок. 5. Позицию цифры в записи числа называют разрядом. 6. Натуральными числаминазываютсячисла, естественным образом используемые при счете. Последовательность всех натуральных чисел, расположенных в порядке их возрастания (1, 2, 3,...), называется натуральным рядом. 7. Расширенным натуральным рядом называется последовательность целых неотрицательных чисел, начинающаяся с нуля (0, 1, 2, 3...). 8. Натуральное число 9. Числа 1 и 10. Делители натурального числа 11. Простымназывается такое число 12. Составным называется такое число 13. Целое число 14. Два неотрицательные целые числа 15. Любое число, большее 1, является простым числом либо разлагается в виде произведения простых чисел одним и только одним способом. 16. Целое число - - 17. НОД совокупности целых чисел 18. НОД взаимно простых чисел 19. Под системой счисления принято понимать способы записи чисел посредством цифровых знаков (цифр) и правила действий над числами. 20. Системы счисления можно разделить на непозиционные и позиционные системы. 21. Непозиционные системы счисления характеризуются тем, что каждый знак (из совокупности знаков, принятой в данной системе для обозначения чисел) всегда обозначает одно и то же число независимо от места (позиции), занимаемого этим знаком в записи числа. 22. В позиционных системах один и тот же знак может обозначать различные числа в зависимости от места (позиции), занимаемым этим знаком в записи числа. 23. Количество различных цифр, применяемых в позиционной системе счисления (ПСС), называют ее основанием. 24. Элементарными цифрами произвольной 25. Каждая позиция числа с присвоенным ей порядковым номером называетсяразрядом числа. 26. В любой 27. Вычетом числа 28. Для перевода целого числа из одной позиционной системы в другую его надо последовательно разделить на основание 29. В настоящее время наибольшее применение находят двоично-степенные системы счисления, основаниями которых являются числа 30. Обобщением двоично-степенных систем счисления являются 31. Два целых числа 32. Вычеты положительных чисел по модулю 33. Вычеты отрицательных чисел по модулю 34. Если два числа 35. Элемент 36. Совокупность классов вычетов 37. В полной системе ненулевых вычетов по модулю
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.244.216 (0.176 с.) |
 делится на натуральное число
делится на натуральное число  , если найдется такое натуральное число
, если найдется такое натуральное число  , что
, что  Делимость числа
Делимость числа  .
. , которое делится лишь на 1 и само на себя, т.е. имеет только несобственные делители.
, которое делится лишь на 1 и само на себя, т.е. имеет только несобственные делители. называется общим делителем целых чисел
называется общим делителем целых чисел  если каждое из этих чисел делится на
если каждое из этих чисел делится на 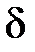 .
. и
и 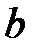 называются взаимно простыми, если их единственным общим делителем является единица.
называются взаимно простыми, если их единственным общим делителем является единица.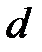 называется наибольшим общим делителем (НОД) целых чисел
называется наибольшим общим делителем (НОД) целых чисел 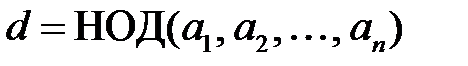 или просто
или просто  .
. ичной позиционной системы счисления являются цифры от 0 (нуля) до
ичной позиционной системы счисления являются цифры от 0 (нуля) до  , где
, где 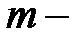 ичной позиционной системе счисления основание системы записывается в виде комбинации цифр 10.
ичной позиционной системе счисления основание системы записывается в виде комбинации цифр 10. по модулю
по модулю  называется разность
называется разность 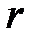 между числом
между числом  , где
, где  есть целая часть отношения
есть целая часть отношения  , т.е.
, т.е.  .
. той системы, в которую оно переводится. При этом основание
той системы, в которую оно переводится. При этом основание  , где
, где  натуральное число.
натуральное число.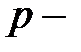 ично степенные системы, в которых основание систем счисления
ично степенные системы, в которых основание систем счисления  , где
, где  натуральное число.
натуральное число. и
и  называют сравнимыми по модулю
называют сравнимыми по модулю 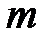 , если одинаковыми являются их вычеты по модулю
, если одинаковыми являются их вычеты по модулю  .
.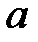 и
и  при делении на модуль
при делении на модуль 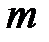 образуют один и тот же остаток
образуют один и тот же остаток  , то относительно их говорят, что эти числа принадлежат одному и тому же классу вычетов
, то относительно их говорят, что эти числа принадлежат одному и тому же классу вычетов  по модулю
по модулю  , принадлежащий множеству вычетов по простому модулю
, принадлежащий множеству вычетов по простому модулю  , называется квадратичным вычетом (невычетом) по модулю
, называется квадратичным вычетом (невычетом) по модулю  , что
, что  .
. образует полную систему вычетов по модулю
образует полную систему вычетов по модулю  , представители которой (числа
, представители которой (числа  ) принадлежат множеству
) принадлежат множеству  , где
, где  простое число.
простое число. , обозначаемой
, обозначаемой  , половина из них будет квадратичными вычетами, а другая половина — квадратичными невычетами.
, половина из них будет квадратичными вычетами, а другая половина — квадратичными невычетами. равна количеству положительных целых чисел, меньших
равна количеству положительных целых чисел, меньших  и взаимно простых с
и взаимно простых с  , для любого
, для любого  .
. , то функция Эйлера
, то функция Эйлера  , все элементы которой
, все элементы которой  принадлежат множеству
принадлежат множеству  , т.е.
, т.е. 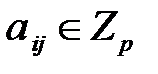 , причем
, причем  простое число, и, кроме того, любые алгебраические преобразования над элементами матриц завершаются приведением их к остатку по модулю
простое число, и, кроме того, любые алгебраические преобразования над элементами матриц завершаются приведением их к остатку по модулю 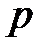 . Такие матрицы называют еще матрицами над полем Галуа характеристики
. Такие матрицы называют еще матрицами над полем Галуа характеристики  .
.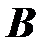 порядка
порядка  называется матрица
называется матрица  , элемент
, элемент  которой, расположенный в i -й строке и j -м столбце, равен остатку по модулю
которой, расположенный в i -й строке и j -м столбце, равен остатку по модулю  от суммы произведения элементов i -й строки матрицы
от суммы произведения элементов i -й строки матрицы 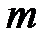 равно единичной матрице.
равно единичной матрице.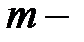 взаимно простые числа, то матрица
взаимно простые числа, то матрица 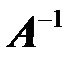 .
. , так как в противном случае
, так как в противном случае  не гарантируется существование определителя модульной матрицы
не гарантируется существование определителя модульной матрицы  , образованная замещением элементов
, образованная замещением элементов  матрицы
матрицы  .
.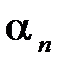 равен единице, называется унитарным (нормированным или приведенным).
равен единице, называется унитарным (нормированным или приведенным). , при котором данный полином
, при котором данный полином  делит без остатка двучлен
делит без остатка двучлен  .
. можно заменить на
можно заменить на 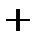 .
. является примитивным элементом расширенного поля
является примитивным элементом расширенного поля  характеристики
характеристики  .
. содержит все ненулевые элементы поля расширенного поля Галуа
содержит все ненулевые элементы поля расширенного поля Галуа  полином
полином 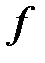 степени
степени  характеристики
характеристики  (необходимые условия), порождающий расширенное поле Галуа
(необходимые условия), порождающий расширенное поле Галуа 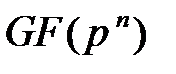 , минимальный примитивный элемент которого
, минимальный примитивный элемент которого  совпадает с характеристикой поля
совпадает с характеристикой поля  , начиная с нулевой степени, приведенных к остатку по модулю неприводимого полинома
, начиная с нулевой степени, приведенных к остатку по модулю неприводимого полинома 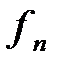 характеристики
характеристики 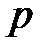 , называется мультипликативной последовательностью, формируемой элементом
, называется мультипликативной последовательностью, формируемой элементом 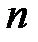 .
.


