
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналіз і синтез систем на основі імітаційного моделювання
Широкий розвиток комп'ютеризації як самого транспорту, так і управління ним неможливий без застосування ефективних наукових методів аналізу і оптимізації складних транспортних систем. Адже завдяки цим методам вдається в повному обсязі реалізувати великі потенційні можливості як прогресивних технологій, так і передової техніки. До таких високоефективних методів належить машинна імітація як особлива форма провадження експериментів на ЕОМ з математичними моделями, що з певним ступенем достовірності описують закономірності функціонування реальних систем і об'єктів. Машинна імітація (імітаційне моделювання) як метод вирішення складних проблем виникла дещо пізніше, ніж було створено перші електронно-обчислювальні машини. Становлення машинної імітації як наукової дисципліни припало на кінець 50-х - початок 60-х років XX століття. Перші публікації з цієї проблематики належать ученим США. У цій країні вперше було практично застосовано метод машинної імітації, зокрема у військовій справі. Наприклад, ракетне командування армії США протягом 1968 фінансового року витратило на дослідження засобами машинного моделювання 74 млн. дол. У колишньому Радянському Союзі дослідження в галузі машинної імітації проводилися з початку 60-х років. Значний внесок у розвиток цієї науки зробив відомий вчений М.П. Бусленко [18]. Йому належать і перші публікації з відповідних проблем. Розвитку машинної імітації відчутно сприяли праці українських учених, зокрема В.М. Глушкова, М.І. Коваленка, М.В. Яворицького та інших. І сьогодні в Україні маємо певні досягнення як у розробці методології машинної імітації, так і у практичному використанні цього методу для вирішення важливих наукових і народногосподарських задач. Особливістю машинних експериментів порівняно з натурним є "програвання" на ЕОМ ситуацій, що імітують функціонування об'єктів і процесів на доволі широкому діапазоні змінювання параметрів і факторів систем без будь-яких обмежень на їх значення. Такі досліди, не потребуючи значних коштів, відкривають необмежені можливості отримання результативної інформації. Особливо цінні такі дослідження в інтерактивному режимі, коли в діалозі з ЕОМ фахівці розширюють свій досвід і розвивають інтуїцію, завдяки чому концептуально коригують імітаційну модель і адаптують її з урахуванням свіжої інформації.
Експериментатор дістає змогу в ході досліджень аналізувати проміжні результати, змінювати ті чи інші управляючі параметри, а отже, і напрямок процесу, що вивчається. Як інструмент експериментального дослідження складних систем машинна імітація охоплює методологію створення моделей систем, методи алгоритмізації та засоби програмних реалізацій імітаторів, планування організацію і виконання на ЕОМ експериментів з імітаційними моделями машинну обробку даних і аналіз результатів. При цьому динамічні та стохастичні характеристики реальних процесів відображаються в моделі за допомогою спеціально сконструйованих процедур. 9.1 Загальні питання імітаційного моделювання Динамічні процеси, які відбуваються у транспортних системах, настільки складні й різноманітні, що аналітичні методи дослідження операцій (математичне програмування, теорія масового обслуговування, теорія ігор та ін.), котрі на перший погляд здаються універсальними, насправді часто непридатні для прогнозування та аналізу фактичних ситуацій. Пояснюється це тим, що математичні моделі, які можуть бути реалізовані за допомогою ефективних обчислювальних методів, є надто, спрощеними, а отже не адекватні реальним процесам. Що ж до адекватний математичних моделей, то їх здебільшого не можна реалізувати через труднощі обчислювального характеру. У такому разі часто є сенс застосувати машинну імітацію, що полягає в моделюванні на ЕОМ реальної транспортної системи. Машинна імітація дає користувачеві змогу експериментувати з існуючими і створюваними системами тоді, коли на реальному об'єкті робити цього не можна або немає жодної рації. Такий метод набуває сьогодні особливої ваги, насамперед, як інструмент удосконалення транспортних процесів. Адже за допомогою імітаційних моделей системи розкривається сутність відповідних явищ і процесів за умови, що натурні досліди в реальному середовищі на реальних об'єктах виключаються. З огляду на сказане можна дати таке означення імітаційного моделювання.
Імітаційне моделювання в широкому розумінні є процес конструювання алгоритмічної моделі функціонування реальної системи та експериментування на цій моделі з метою визначення поводження системи або оцінити (в рамках обмежень, зумовлених деяким критерієм чи сукупністю критеріїв) різні стратегії, що забезпечують задане функціонування даної системи У вужчому розумінні імітаційне моделювання - це відтворення на ЕОМ функціонування реальної системи. За такого тлумачення термін "імітаційне моделювання" має той самий сенс, що й "машинна імітація". Щоб застосувати такий метод для досліджень, створюють імітаційну систему, яка містить у собі імітаційну модель, а також внутрішнє і зовнішнє математичне забезпечення. При цьому в ЕОМ вводяться потрібні вхідні дані і спостерігаються зміни показників, котрі у процесі моделювання можуть аналізуватися й піддаватися статистичній обробці. Імітаційна модель - комплексна математична й алгоритмічна модель досліджуваної системи. А метод, що базується на розробці та дослідженні імітаційних моделей, називається машинною імітацією, або імітаційним моделюванням. Термін "машинна імітація", який точніше відбиває сутність проблеми, у вітчизняний літературі використовується рідше, ніж термін "імітаційне моделювання"; у зарубіжний літературі першому терміну відповідають такі: computer simulation - комп'ютерне моделювання, system simulation - системне моделювання, digital simulation - цифрове моделювання. Слово "імітація" походить від англійського imitate - наслідувати, копіювати. Отже, термін "машинна імітація" означає копіювання на ЕОМ реальних чи гіпотетичних процесів. Слово "моделювання" походить від французького modeler - ліпити. Відмітимо основні переваги та недоліки методу імітаційного моделювання: 1. Вдається відповісти на багато запитань, що постають на ранніх стадіях задуму і попереднього проектування систем, уникнувши застосування методу спроб і помилок, котрий пов'язаний зі значними витратами. Зокрема, на підставі аналізу імітаційної моделі можна заздалегідь визначити ефективність функціонування будь-якої проектованої системи й попередити необґрунтовані витрати людських і матеріальних ресурсів на побудову нераціональних систем. 2. Метод дає змогу досліджувати особливості функціонування системи за будь-яких умов, зокрема й тих, котрі не реалізовані в натурних експериментах. При цьому параметри системи і навколишнього середовища можна варіювати в як завгодно широких межах, відтворюючи довільну обстановку. Завдяки такому підходу різко зменшується потреба в складному лабораторному обладнанні та експлуатаційних випробуваннях системи. 3. Стає можливим прогнозувати поводження системи в близькому та віддаленому майбутньому, екстраполюючи на моделі результати промислових випробувань. У такому разі дані, здобуті раніше, поповнюються завдяки застосуванню статистичного підходу. 4. Імітаційні моделі технічних і технологічних систем та пристроїв дають змогу в багато разів скоротити час їх випробування: від днів і місяців у реальних умовах до секунд і хвилин на ЕОМ. Єдиним обмеженням тут можуть бути наявні ресурси машинного часу та пам'яті.
5. За допомогою методу імітаційного моделювання можна штучним шляхом швидко й у великому обсязі дістати потрібну інформацію, що відображає хід реальних процесів, уникнувши дорогих, а часто неможливих натурних випробувань цих процесів. 6. Імітаційна модель є надзвичайно гнучким пізнавальним інструментом, здатним відтворювати довільні як реальні, так і гіпотетичні ситуації, оскільки на неї не поширюються жодні фактичні обмеження. 7. З огляду на те, що дослідження і оптимізацію деяких складних систем не можна виконати ні з допомогою лабораторних чи натурних експериментів, ні аналітичними методами, імітаційне моделювання на ЕОМ часто буває єдиним реалізованим способом розв'язання таких задач. Як недолік слід відмітити, що при введенні некоректних вхідних даних та умов проведення імітаційного моделювання, отримані результати можуть в значний мірі відрізнятися від реальної поведінки системи. Метод Монте-Карло Більшість процесів, що характерні для транспортних систем, значною мірою відбуваються під впливом випадкових факторів, які не підлягають контролю з боку осіб, відповідальних за прийняття і реалізацію рішень у контексті забезпечення оптимального функціонування систем. Проте з позицій системного аналізу врахування невизначеностей є обов'язковим елементом процедури вироблення планово-управлінських рішень. Задача полягає в тому, щоб якомога повніше врахувати вплив неконтрольованих випадкових факторів і зробити в таких умовах аргументований висновок щодо можливих напрямків розвитку системи та оптимальної стратегії нею. Такі задачі розв'язують за допомогою методу Монте-Карло (методу статистичних випробувань). Метод Монте-Карло являє собою сукупність формальних процедур, засобами яких відтворюються на ЕОМ будь-які випадкові фактори (випадкові події, випадкові величини з довільним розподілом, випадкові вектори тощо). Зауважимо, що «розігрування» вибірок за методом Монте-Карло є основним принципом імітаційного моделювання систем зі стохастичними (випадковими, імовірними) елементами. Зародження методу Монте-Карло пов'язане з дослідженнями фонНеймана та Улама наприкінці 40-х років, коли вони запровадили термін «метод Монте-Карло» і застосували цей метод до розв'язування деяких задач екранування ядерних випромінювань. Згаданий математичний метод був відомий давно, проте пережив своє друге народження, коли знайшов у Лос-Аламосі (США) застосування в закритих роботах з ядерної техніки, виконуваних під кодовою назвою «Монте-Карло». Результати були настільки успішними, що цей метод швидко поширився і в інших галузях науки і техніки. Для багатьох фахівців термін «метод Монте-Карло» є синонімом терміна «імітаційне моделювання». І хоча вибірковий метод Монте-Карло є найбільш корисним при моделюванні стохастичних ситуацій, він придатний також і для розв'язання деяких цілком детермінованих задач, що не мають аналітичних розв'язків.
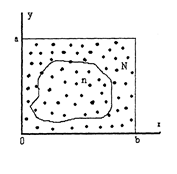
Одним з найбільш поширеним прикладом застосування методу Монте- Рис.9.1 Визначення площі методом Монте-Карло Карло є визначення площі чи об'єму геометричних фігур, що не мають аналітичного виразу оточуючих фігуру границь. Розглянемо простий випадок. Нехай потрібно визначити площу фігури довільної форми, що не має аналітичного виразу (див. рис.9.1). Якщо на площі прямокутника (a x b) генерувати N точок з випадковими координатами у і х, що підкоряються рівномірному закону розподілу ймовірностей, і підраховувати кількість точок, як належать саме фігурі (n), то при великій кількості точок N можна стверджувати, що площа цієї фігури може бути визначена як: Рис.9.1 Визначення площі методом Монте-Карло
Очевидно, що такий спосіб визначення площі не потребує знання аналітичного виразу границь фігури. Головним при цьому є лише необхідність генерування послідовності N випадкових чисел, які підкоряються рівномірному закону розподілу ймовірності їх появи. Алгоритм аналізу кожної пари координат (уi і хi) є при цьому дуже простим: чи належить цяточка фігурі чи ні. Очевидно також, що точність визначення S цілком залежить від кількості генерованих точок N В теорії методу статистичних випробувань приводиться, що похибка результату визначається як Не менш важливим є правильний вибір закону розподілу ймовірностей появи певних чисел у випадкової послідовності. Наприклад, якщо в розглянутому раніше випадку при генеруванні випадкової послідовності координат точок не з рівномірним, а з нормальним законом розподілу їх відхилень від центру прямокутника, відношення n/N являє собою вже характеристику точності попадання у центр прямокутника, а аж ніяк не визначатиме площу фігури. Відмітимо, що саме необхідність генерування випадкової послідовності чисел з заданим законом їх розподілу, який відповідає реальним процесам, що протікають у реальній системі, є основною задачею імітаційного моделювання, а точність генерування заданого закону розподілу випадкових величин у значний мірі обумовлює точність результатів імітаційного моделювання.
Види випадкових потоків При розгляді випадкових процесів, які протікають в системах з дискретними станами і безперервним часом, часто доводиться стикатися з так званими «потоками подій». Потоком подій називається послідовність однорідних подій, які слідують одне за одним у випадкові моменти часу. Прикладами можуть бути: —потік вимог на телефонній станції; —потік вантажів, які поступають у складські приміщення; —автомобілів, що надходять на АЗС, і т. ін. При розгляді процесів, які протікають в системі з дискретними станами і безперервним часом, часто буває зручно уявити собі процес так, буцімто переходи системи із стану в стан проходять під дією якихось потоків подій (потік вимог, потік несправностей, потік заявок на обслуговування, потік відвідувачів і т. п.) Будемо зображувати потік подій послідовністю точок на осі часу 0t (рис.9.2).
Рис.9.2. Зображення потоку на часовій осі
Користуючись таким зображенням, слід пам'ятати, що положення кожної точки на осі 0t випадкове. Потік подій зветься регулярним, якщо події слідують одне за одним через строго визначені проміжки часу. Такий потік порівняно рідко зустрічаються на практиці, але являє собою визначений інтерес як граничний випадок. Частіше приходиться зустрічатися з потоками подій, для яких і моменти появи подій і проміжки часу між ними випадкові. 1. Потік подій зветься стаціонарним, якщо імовірність потрапляння того чи іншого числа подій на ділянку часу довжиною т (рис.9.2) залежить тільки від довжини ділянки і не залежить від того, де саме на осі 0t розташована ця ділянка. 2. Потік подій називається потоком без післядії, якщо для будь-яких ділянок часу, які не перетинаються, число подій, які потрапляють на один із них, не залежить від того, скільки подій потрапило на другу (або іншу, якщо розглядається більше двох ділянок). 3. Потік подій зветься ординарним, якщо імовірність потрапляння на елементарну ділянку двох або більше подій мала на стільки, що нею можна знехтувати в порівнянні з імовірністю потрапляння на неї однієї події. Розглянемо більш детально ці три властивості потоків. Стаціонарність потоку означає його однорідність в часі; імовірнісні характеристики такого потоку не повинні змінюватися залежно від часу. Зокрема, інтенсивність потоку подій — середнє число подій в одиницю часу — для стаціонарного потоку повинна залишатися постійною. Зрозуміло, це не означає, що фактична кількість подій, які з'являються в одиницю часу, постійна. Потік може мати місцеві згущення і розрідження. Важливо, що для стаціонарного потоку ці згущення і розрідження не носять закономірного характеру, а середнє число подій, які потрапляють на одиничну ділянку часу, залишається постійним для усього періоду, який розглядається. На практиці часто зустрічаються потоки подій, які (принаймні, на обмеженій ділянці часу) можуть розглядатися як стаціонарні. Наприклад, потік вимог, які потрапляють на телефонну станцію, скажемо, на інтервалі від 12 до 13 годин може вважатися стаціонарним. Той же потік на протязі цілої доби вже не буде стаціонарним (вночі інтенсивність потоку вимог набагато менша, ніж у день). Відсутність післядії в потоці означає, що події, які утворюють потік, з'являються в послідовні моменти часу незалежно одна від одної. Наприклад, потік пасажирів, які входять на станцію метро, можна вважати потоком без післядії, тому що причини, які обумовлюють прихід окремого пасажира саме в даний момент, а не в іншій, як правило, не зв'язані з аналогічними причинами для інших пасажирів. Ординарність потоку означає, що події в потік потрапляють поодинці, а не парами, трійками і т. п. Наприклад, потік клієнтів, які прямують до перукарні, практично можна вважати ординарним, чого не можна сказати про потік клієнтів, які прямують до ЗАГСу для реєстрації шлюбу. Потік атак винищувачів на бомбардувальник, який знаходиться над ворожою територією, ординарний, якщо вони атакують ціль поодинці, і не ординарний, якщо вони атакують парами або трійками. Якщо в неординарному потоці події відбуваються тільки парами, тільки трійками і т.д., то можна його розглядати як ординарний «потік пар», «потік трійок» і т. д. Якщо потік подій не має післядії, ординарний, але не стаціонарний, він називається нестаціонарним пуассонівським потоком. Розглянемо потік подій, який володіє всією трійкою властивостей: стаціонарний, без післядії, ординарний. Такий потік зветься простішим (або стаціонарним пуассонівським) потоком. Назва «простіший» пов'язана з тим, що математичний опис подій, пов'язаних з простішими потоками виявляється найбільш простою. Відмітимо також, що простіший потік відіграє серед інших потоків особливу роль. Якщо потік подій не має післядії, ординарний, але не стаціонарний, вінназивається нестаціонарним пуассонівським потоком. В такому потоці інтенсивність λ, (середнє число подій в одиницю часу) залежить відчасу λ= λ(t), тоді, як для простішого потоку λ= const. Пуассонівський потік подій (як стаціонарний, так і нестаціонарний) тісно пов'язаний з відомим розподілом Пуассона. Окремим випадком пуассонівського закону розподілу, який описує ймовірність появи на інтервалі часу t певного числа подій, є експоненційний (показовий) закон розподілу, що описує ймовірність появи певного інтервалу часу між двома сусідніми подіями. F(t) = 1-λe-λt (t >0) (9.1)
Щільність розподілу часових інтервалів f(t) визначається формулою: f(t) = λe-λt (t >0) (9.2)
Величина X називається параметром експоненційного закону розподілу. Числові характеристики цього закону розподілу: математичне сподівання тt і дисперсія Dt визначаються формулами:
Середньоквадратичне відхилення випадкової величини від математичного очікування:
завжди дорівнює математичному очікуванню. Те ж саме стосується і їх оцінок, отриманих по результатах експерименту, що дозволяє зробити дуже важливий практичний висновок: якщо експериментальні оцінки середньоквадратичного відхилення і математичного очікування рівні, то в якості моделі такого потоку можна прийняти розподіл Пуассона. Недоліком експоненціального розподілу є те, що щільність експоненціального розподілу монотонно спадає, починаючи з максимального значення, визначеного для t=0, тобто імовірність появи інтервалу між двома фіксованими інтервалами зростає, коли ці значення наближаються до нуля. Але при дослідженні інтервалів часу між двома подіями часто зручно мати щільність розподілу, яка проходить через початок координат. Це відповідає тому, що імовірність коротких інтервалів дуже мала. Найбільш придатною моделлю подібних потоків подій є потоки Ерланга, які часто називають потоками з післядією. Ці потоки утворюються в результаті «просіювання» простіших потоків. Розглянемо на осі простіший потік подій (рис.9.3) і збережемо в ньому не всі точки, а тільки кожну другу, інші відкинемо (на рис.9.3), точки, які ми зберігаємо, показані жирними. В результаті такої операції «розрідження» або «просіювання» утворюється інший потік подій; який називається потоком Ерланга другого порядку.
Рис.9.3 Приклад формування потоку Ерланга 2-го порядку
Взагалі, потоком Ерланга к-го порядку називається потік, який утворюється, якщо в простішому потоці зберегти кожну к-ту точку, а решту відкинути. Щоб визначити, як розподіляються проміжки часу між подіями в потоці Ерланга k-ro порядку, необхідно встановити закон розподілу. Закон розподілу інтервалу часу Т між сусідніми подіями в потоці Ек називається законом Ерланга к-то порядку:
де fkt - імовірність очікування тривалістю t для k-гo прибуття або здійснення k-ї; k, - параметр розподілу Ерланга; k - ціле додатне число; Λк - інтенсивність подій вхідного потоку. Виразимо інтенсивність Λк та дисперсію самого потоку Ерланга через інтенсивність породжуючого його вхідного потоку λ: Λк= λ/ k; λ= k Λк (9.7)
При цьому середній інтервал часу між подіями та його середньо-квадратичне відхилення визначаються як
З цих формул слідує, що при необмеженому зростанні параметра к Т=1/Λк – const. (9.9)
Ця властивість потоків Ерланга зручна при практичному використанні: задаючись різними к, можна отримувати потоки, яким притаманна різна післядія - від цілковитої відсутності післядії (k=1) дожорсткого функціонального зв'язку між моментами появи подій
9.4 Методи генерування потоків подій з різними законами розподілу ймовірностей Практично усі випадкові потоки подій мають у своїй основі потік з рівномірним законом розподілу ймовірностей, котрий далі трансформується в потік з будь-яким законом розподілу. Тому розглянемо більш детально властивості і алгоритм формування саме цього потоку. Перш за все, це є потік рівномірно розподілених випадкових чисел, значення яких належать відрізку [0, 1]. Опишемо властивості цих чисел. Нагадаємо, що випадкова величина X має рівномірний розподіл на відрізку [0, 1]. Щільність розподілу ймовірностей має вигляд:
Математичне очікування та дисперсія такого розподілу: тх=\/2; σ2x =1/12. В ЕОМ генерування потоку випадкових чисел, що мають такий закон розподілу, здійснюється за допомогою оператора " rnd ". Практично при цьому застосовується досить проста процедура: ui+1 = FRAC(k · и.), де k = 8t ± З, t - непарне ціле число.
Часто застосовують значення t=5, k =37 або k=39. При цьому необхідно задавати довільне початкове значення u0 < 0. Отримана таким чином послідовність чисел у достатньо великій кількості буде розподілена рівномірно на інтервалі [0,1]. Отримана послідовність не є чисто випадковою, тому що застосовує детермінований алгоритм генерації. Це означає, що числа будуть випадковими лише протягом одної послідовності. При повторі вони, строго кажучи, будуть повторюватись, якщо не змінити початкове значення u0. Щоб запобігти цьому явищу, застосовують оператор " randomize " з метою випадкового варіювання значення u0. Для генерування випадкової рівномірно розподіленої послідовності чисел в будь якому інтервалі [а,b] застосовують трансформацію генерованої послідовності иi (і =
Випадкові послідовності, що є розподілені по нормальному (гаусовському) закону розподілу, отримуються звичайно трансформацією послідовності з рівномірним розподілом за допомогою формул:
При цьому генерується послідовність нормально розподілених чисел, що мають математичне очікування mR=0 і дисперсію σ2R=l. При інших значеннях mR і σ2R цю послідовність трансформують наступним чином:
При необхідності генерувати потік Пуассона з експоненційним законом розподілу часових інтервалів між подіями у потоці, послідовність з рівномірним розподілом трансформується за допомогою наступної формули:
Величина (1-ui) також має рівномірний розподіл на відрізку [0,1]. Тому вираз для xi можна написати простіше:
При моделюванні потоків Ерланга випадкову величину хі можна розіграти по формулі, запропонованій у книзі проф. Соболя І.М[8]:
де и1 ≤ u2 ≤... ≤ ик - випадкові числа отримані оператором "rnd" в діапазоні [0, 1]), при умові їх розташування в порядку зростання. Саме необхідність впорядкування потоку чисел иi
Зауважимо, що при застосуванні цього методу немає необхідності ранжирувати початковий потік, що значно спрощує задачу генерації. В таблиці 9.1 наведені чисельні характеристики потоків, отриманих за допомогою вказаних методів. Там же наведені результати формування потоку шляхом простого просіювання.
Таблиця 9.1 Порівняльна характеристика різних методів генерування потоків Ерланга (А=1)
Порівняння результатів свідчить про те, що просте просіювання не дає задовільного результату. Обидва інші методи майже рівнозначні, за винятком к=1. Далі, при розробці програми імітаційного моделювання систем масового обслуговування з непуоссонівськими потоками заявок буде передбачена можливість застосування як одного, так і другого методу генерування потоків Ерланга. Але при к=1 доцільніше користуватись стандартною процедурою генерування потоку Пуассона.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.55 (0.087 с.) |

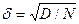 , де D – певна константа. Очевидно, що збільшення точності результату потребує збільшення кількості генерованих випадкових чисел у 100 разів. Саме необхідність генерування значної кількості випадкових чисел і є суттєвим недоліком цього методу. Вважається, що 90% задачі імітаційного моделювання систем приходиться саме на генерування випадкової послідовності чисел з заданим розподілом ймовірності і тільки 10% - на моделювання алгоритму функціонування системи.
, де D – певна константа. Очевидно, що збільшення точності результату потребує збільшення кількості генерованих випадкових чисел у 100 разів. Саме необхідність генерування значної кількості випадкових чисел і є суттєвим недоліком цього методу. Вважається, що 90% задачі імітаційного моделювання систем приходиться саме на генерування випадкової послідовності чисел з заданим розподілом ймовірності і тільки 10% - на моделювання алгоритму функціонування системи.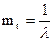 (9.3)
(9.3)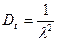 (9.4)
(9.4)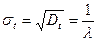 (9.5)
(9.5)
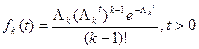 (9.6)
(9.6)

 (9.8)
(9.8)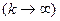 середньоквадратичне відхилення прямує до нуля, тобто розкид статистичних характеристик зменшується. Це означає, що при зростанні параметра к
середньоквадратичне відхилення прямує до нуля, тобто розкид статистичних характеристик зменшується. Це означає, що при зростанні параметра к 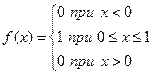 (9.10)
(9.10)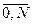 ) за допомогою формули:
) за допомогою формули:

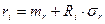
 (9.11)
(9.11)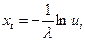 (9.12)
(9.12) (9.13)
(9.13)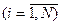 робить цей метод дещо складним. Тому в [5] запропоновано новий метод трансформації випадкових чисел, отриманих оператором "rnd" в діапазоні [0, 1]), а саме за допомогою формули:
робить цей метод дещо складним. Тому в [5] запропоновано новий метод трансформації випадкових чисел, отриманих оператором "rnd" в діапазоні [0, 1]), а саме за допомогою формули: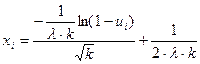 (9.14)
(9.14)


