Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем. Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем: Þ
Выражение (2.3.2) - обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ¹ 0. Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0). Требуется найти y(t) при известных начальных условиях. Из курса “Математика” известно, что
В курсе «УТС» будем называть решение однородного дифференциального уравнения Вторую составляющую решения (2.3.3) будем называть
Напомним “этапы” решения: 1) Если имеется уравнение вида
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на ЭВМ) находим корни характеристического уравнения 4) Тогда собственное решение записывается в виде:
если среди l j нет повторяющихся корней (кратность корней равна 1). Если уравнение (2.3.5) имеет 2 (два) совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы: а) По виду правой части. б) Методом вариации постоянных. в) Другие методы… Если вид правой части дифф. уравнения – относительно несложная функция времени, то предпочтительным является способ а)…Þ «подбор» решения… Þ 6) Суммируя полученные составляющие (собственную и вынужденную), имеем: Þ
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования
Пример: Найти аналитическое выражение переходного процесса на выходе звена, если Þ
Решение. Þ Запишем однородное ОДУ Þ
где С 1 и С 2 - неизвестные (пока) постоянные интегрирования. По виду временной функции в правой части запишем
Подставляя в исходное уравнение, имеем: Þ
Суммируя Используя 1-е начальное условие (при t = 0), получаем: Решая систему линейных уравнений относительно С 1 и С 2, имеем: ==> С 1 = -1/6; C 2 = -4/3. Тогда окончательно:
На рис. 2.7 приведено сравнение аналитического решения по вышеприведенному соотношению (сплошная линия) и численного решения задачи (пунктирная линия) в среде программного комплекса «Моделирование в технических устройствах» (ПК «МВТУ»).
Рис. 2.7 – Сравнение аналитического и численного решений уравнения динамики
|
|||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.130.13 (0.007 с.) |

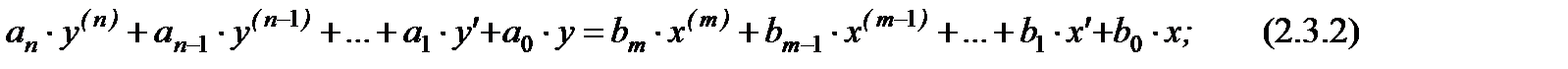
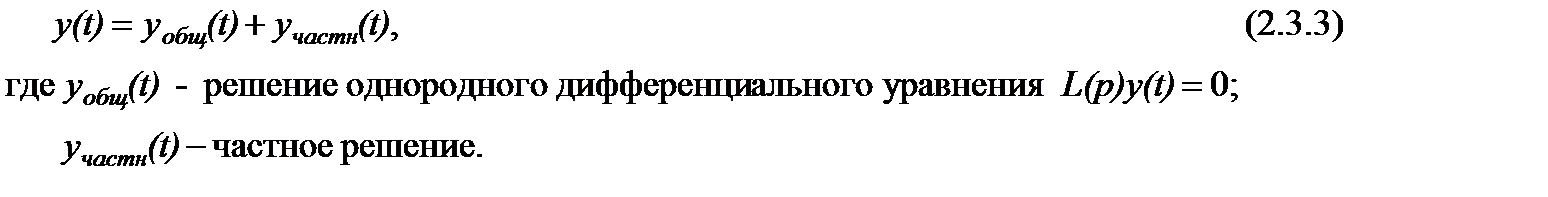
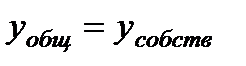 , так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).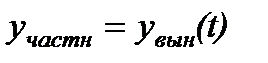 , так как эта часть решения определяется внешним воздействием x(t), поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие. Þ
, так как эта часть решения определяется внешним воздействием x(t), поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие. Þ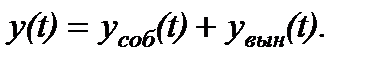 (2.3.4)
(2.3.4)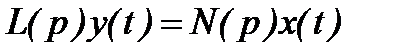 , то сначала решаем однородное дифференциальное уравнение:
, то сначала решаем однородное дифференциальное уравнение: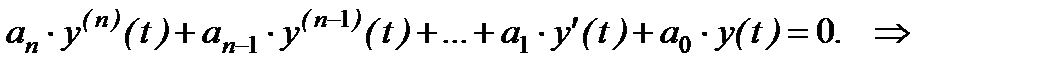
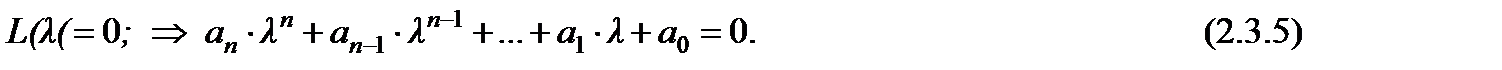
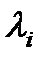 . Þ
. Þ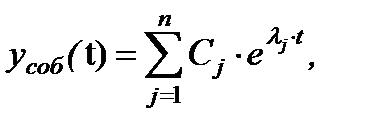 (2.3.6)
(2.3.6)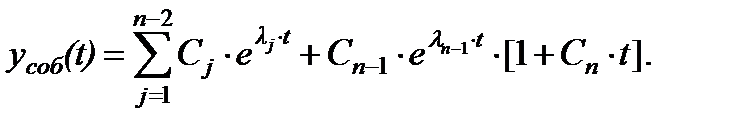 (2.3.7)
(2.3.7)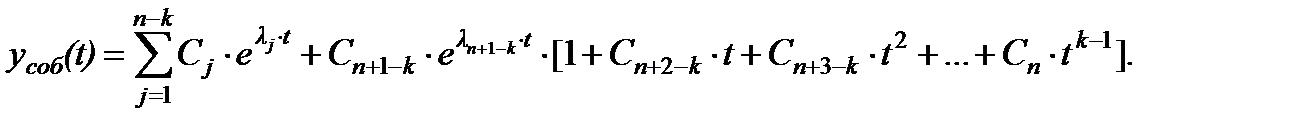 (2.3.8)
(2.3.8)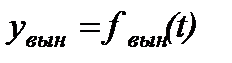 .
.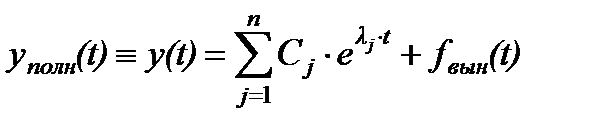 Þ
Þ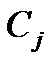 . Þ Обычно получается система алгебраических уравнений. Þ Решая систему, находим значения постоянных интегрирования
. Þ Обычно получается система алгебраических уравнений. Þ Решая систему, находим значения постоянных интегрирования 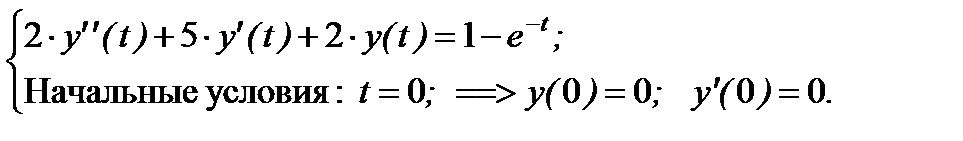
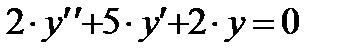 Þ Характеристическое уравнение Þ
Þ Характеристическое уравнение Þ 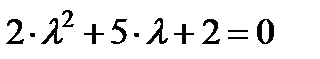 ; Þ Решая, имеем: Þ
; Þ Решая, имеем: Þ 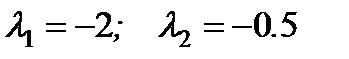 Þ
Þ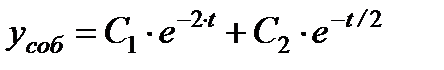 ,
,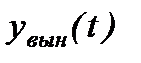 как:
как: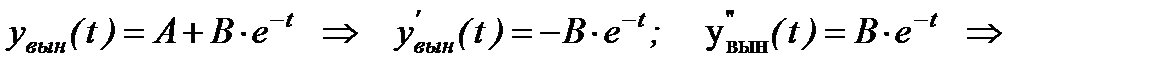
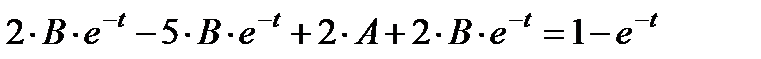 Þ
Þ 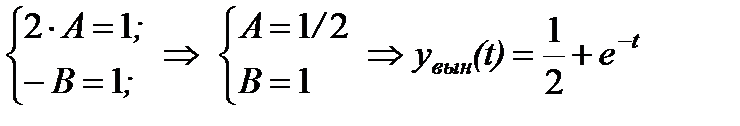
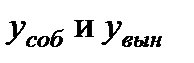 , имеем: Þ
, имеем: Þ 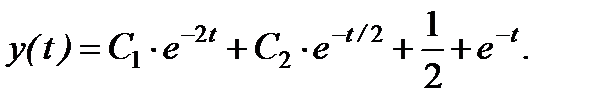
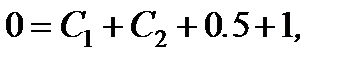 а из 2-го начального условия имеем:
а из 2-го начального условия имеем: 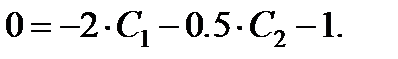
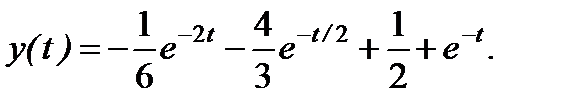 (*)
(*)