Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура систем управления: простые и многомерные системыСтр 1 из 16Следующая ⇒
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УПРАВЛЕНИЯ ТЕХНИЧЕСКИМИ СИСТЕМАМИ
1.1. Цели, принципы управления, виды систем управления, основные определения, примеры
Развитие и совершенствование промышленного производства (энергетики, транспорта, машиностроения, космической техники и т.д.) требует непрерывного увеличения производительности машин и агрегатов, повышения качества продукции, снижения себестоимости и, особенно в атомной энергетике, резкого повышения безопасности (ядерной, радиационной и т.д.) эксплуатации АЭС и ядерных установок. Реализация поставленных целей (см. выше) не возможна без внедрения современных систем управления, включая как автоматизированных (с участием человека-оператора), так и автоматических (без участия человека-оператора) систем управления (СУ-аббревиатура). Определение: Управление - это такая организация того или иного технологического процесса, которая обеспечивает достижение поставленной цели. Теория управления является разделом современной науки и техники. Она базируется (основывается) как на фундаментальных (общенаучных) дисциплинах (например, математика, физика, химия и т.д.), так и на прикладных дисциплинах (электроника, микропроцессорная техника, программирование и т.д.). Любой процесс управления (автоматического) состоит из следующих основных этапов (элементов): § получение информации о задаче управления; § получение информации о результате управления; § анализ получаемой информации; § выполнение решения (воздействие на объект управления). Для реализации Процесса Управления система управления (СУ) должна иметь: § источники информации о задаче управления; § источники информации о результатах управления (различные датчики, измерительные устройства, детекторы и т.д.); § устройства для анализа получаемой информации и выработки решения; § исполнительные устройства, воздействующие на Объект Управления, содержащие: регулятор, двигатели, усилительно-преобразующие устройства и т.д. Определение: Если система управления (СУ) содержит все перечисленные выше части, то она является замкнутой. Определение: Управления техническим объектом с использованием информации о результатах управления называется принципом обратной связи.
Схематично такая система управления может быть представлена в виде:
Рис. 1.1 - Структура системы управления (СУ) Если система управления (СУ) имеет структурную схему, вид которой соответствует рис. 1.1, и функционирует (работает) без участия человека (оператора), то она называется системой автоматического управления (САУ). Если СУ функционирует с участием человека (оператора), то она называется автоматизированной СУ. Если Управление, обеспечивает заданный закон изменения объекта во времени независимо от результатов управления, то такое управление совершается по разомкнутому циклу, а само управление называется программным управлением. К системам, работающим по разомкнутому циклу, относятся промышленные автоматы (конвейерные линии, роторные линии и т.д.), станки с числовым программным управлением (ЧПУ): см. пример Þ
Рис.1.2 - Пример программного управления Задающее устройство может быть, например, и “копиром”. Поскольку в данном примере нет датчиков (измерителей), контролирующих изготавливаемую деталь, то если, например, резец был установлен неправильно или сломался, то поставленная цель (изготовление детали) не может быть достигнута (реализована). Обычно в системах подобного типа необходим выходной контроль, который будет только фиксировать отклонение размеров и формы детали от желаемой. Автоматические системы управления подразделяются на 3 типа:
САР и СС являются подмножествами САУ Þ {САР}Î{САУ}; {СC}Î{САУ}. Определение: Автоматическая система управления, обеспечивающая постоянство какой-либо физической величины (группы величин) в объекте управления называется системой автоматического регулирования (САР). Системы автоматического управления (САР) - наиболее распространенный тип систем автоматического управления.
Первый в мире автоматический регулятор (18-е столетие) - регулятор Уатта. Данная схема (см. рис. 1.3) реализована Уаттом в Англии для поддержания постоянной скорости вращения колеса паровой машины и, соответственно, для поддержания постоянства скорости вращения (движения) шкива (ремня) трансмиссии. В данной схеме чувствительными элементами (измерительными датчиками) являются “грузы” (сферы). «Грузы» (сферы) также “заставляют” перемещаться коромысло и затем задвижку. Поэтому данную систему можно отнести к системе прямого регулирования, а регулятор - к регулятору прямого действия, так как он одновременно выполняет функции и “измерителя” и “регулятора”. В регуляторах прямого действия дополнительного источника энергии для перемещения регулирующего органа не требуется.
Рис. 1.3 - Схема автоматического регулятора Уатта В системах непрямого регулирования необходимо присутствие (наличие) усилителя (например, мощности), дополнительного исполнительного механизма, содержащего, например, электродвигатель, серводвигатель, гидропривод и т.д. Примером САУ (системы автоматического управления), в полном смысле этого определения, может служить система управления, обеспечивающая вывод ракеты на орбиту, где управляемой величиной может быть, например, угол между осью ракеты и нормалью к Земле Þ см. рис. 1.4.а и рис. 1.4.б Þ ПРИМЕР СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ – ЗАПУСК РАКЕТЫ
Рис.1.4.а Рис.1.4.б Примером СС (следящей системы) может служить радиолокационная система слежения за движением “неизвестного” самолета, поскольку “маневры” самолета заранее неизвестны, поэтому и закон перемещения антенны во времени заранее неизвестен.
Основные законы управления
Если вернуться к последнему рисунку (структурная схема САУ на рис. 1.7), то необходимо “расшифровать” роль, которую играет усилительно-преобразующее устройство (какие функции выполняет). Þ Если усилительно-преобразующее устройство (УПУ) выполняет только усиление (или ослабление) сигнала рассогласования e(t) Þ Если УПУ выполняет формирование выходного сигнала e1(t), пропорционального ошибке e(t) и интегралу от e(t), т.е. Обычно ПИ-управление используется для повышения точности управления (регулирования). Если УПУ формирует выходной сигнал e1(t) пропорциональный ошибке e(t) и ее производной, то такой режим называется пропорционально-дифференцирующим (ПД-управление). Þ Обычно использование ПД-управления повышает быстродействие САУ. Если ПИД-управление позволяет зачастую обеспечить “хорошую” точность управления при “хорошем” быстродействии (малом времени переходных процессов). Линейное воздействие
Данный вид входного воздействия используется для оценки точности систем управления, а именно, для определения скоростных ошибок.
x(t) = a∙t, (2.4.7) где t ³ 0, а при t < 0 входное воздействие всегда равно нулю. На рисунке 2.14 представлен график линейного входного воздействия.
Рисунок 2.14 – Линейное входное воздействие
2.5. Основные положения и свойства интегральных преобразований Лапласа
Решение однородного обыкновенного дифференциального уравнения (ОДУ) усоб(t) записывается в виде (если нет повторяющихся корней):
т.е. все члены уравнения имеют одну и ту же форму. Этот результат наводит на мысль, а нельзя ли ввести какое-то преобразование, в результате которого уравнение динамики (дифференциальное) можно привести к чисто алгебраическому, решение которого не представляет проблем. А если затем сделать соответствующее обратное преобразование, то получим у соб (t). Þ Þ Обыкновенное дифференциальное уравнение (ОДУ) ® Алгебраическое уравнение Þ Решение Þ ® Обратное преобразование Þ Результат. Именно такими соображениями руководствовался Лаплас, предлагая такое преобразование, называемое в настоящее время преобразованием Лапласа. Þ Предположим, что имеется нестационарный процесс f(t). Þ Лаплас предложил ввести интегральное преобразование, которое отображает f(t) на комплексную плоскость по соотношению: Þ
iIm
Re
Рисунок 2.15 где s = c+i×w: w Î ] -¥; +¥ [; с – абсцисса абсолютной сходимости (обычно в курсе «УТС» с = 0); f(t) – прообраз (оригинал); F(s) – изображение (образ); Символическое обозначение преобразования Лапласа:
f(t)
Преобразования Лапласа существует, если:
а также при t< 0 f(t)= 0. f (t) iIm F(s) s = s 1 = c+ i×w Þ Re f (t) s = s 2 = c + i×w 2 t s = s 3 = c + i×w 3 s = s 6 s = s 4 s = s 5 Рисунок 2.16 Рисунок 2.17 В соответствии с соотношением (2.5.1) переходной процесс f(t) отображается на комплексную плоскость, где каждому значению оператора Лапласа «s» соответствует свой вектор. Þ Линия, соединяющая концы векторов называется годографом. Обратное преобразование Лапласа определяется следующим соотношением:
Необходимо подчеркнуть, что если условие сходимости выполняется, то любомуоригиналу соответствует изображение. Обратное преобразование Лапласа не всегда существует, т.е. если известно F(s), это не означает, что ему соответствует оригинал f(t)!!!
Прямое преобразование Лапласа символически обозначается:
f(t)
Обратное преобразование Лапласа обозначается: F(s)
Существует двухстороннее преобразование Лапласа LB [f(t)], частным случаем которого является обычное преобразование Лапласа Þ
Если при t £ 0 функция f(t) = 0, то L B [ f(t) ] º L [ f(t) ]. Частным случаем двухстороннего преобразования Лапласа (при с = 0, т.е. s = i×w) является преобразование Фурье, определяемое соотношениями:
2.5.1. Использование преобразования Лапласа для операции дифференцирования
Пусть известно f(t) и его изображение по Лапласу: (f(t) Воспользуемся соотношением (2.5.1) Þ
где f(0) – начальное условие. Если начальные условия равны нулю Þ f(0) = 0;
Аналогичным способом найдем изображение 2-ой производной Þ
Если при t = 0 f(t) и f `(0) равны нулю (нулевые начальные условия), то Þ
Обобщая на производную n -го порядка при нулевых начальных условиях, имеем:
2.5.2. Использование преобразования Лапласа для операции интегрирования
Пусть известно преобразование f(t) Окончательно:
Если начальные условия равные нулю:
2.6. Основные свойства преобразований Лапласа Свойство линейности
Пусть есть процессы f1(t) и f2(t), каждый из которых имеет свое изображение по Лапласу: f1(t)
Если f(t)=a× f1(t), то:
2.6.2. Свойство подобия (свойство изменения масштаба)
Пусть f(t)
Первая предельная теорема
Пусть f(t)
s 0 t
Это означает, что оси «t» и «s» формально направлены в противоположные стороны, т.е. чем больше t, тем меньше s и наоборот.
Вторая предельная теорема Пусть f(t)
2.7. Способы нахождения обратных преобразований Лапласа по известному изображению
Вычисление оригиналов по известному (данному) изображению можно выполнить: - по соответствующим таблицам преобразований Лапласа; - по формулам Хэвисайда; - разложением на элементарные дроби; - и другие способы. В справочниках по «Математике» приводятся довольно обширные таблицы, по которым можно найти оригиналы большинства изображений. Однако, нередко бывают и случаи, когда необходимое преобразование отсутствует в таблицах Þ В этом случае используются различные специальные способы Þ Если изображение F(s) можно представить в виде отношения полиномов по степеням «s», то наиболее общим и эффективным способом поиска оригинала является формула Хэвисайда. Þ если
где sj – полюса изображения, т.е. те значения «s» при которых полином D0(s) обращается в ноль;
kj – кратность j – го полюса Если уравнение D0(s)=0 имеет n различных корней, то это означает что полюса F(s) имеют кратность, равную единице, т.е. нет повторяющихся полюсов. Необходимо отметить, что использование формулы (2.7.1) будет корректно только в том случае, когда степень полинома D0(s) выше степени полинома D1(s). Если степени равны, то необходимо выделить целую часть (разделив «в столбик» полиномы) и чисто дробную часть, после чего для чисто дробной части корректна формула (2.7.1). В качестве иллюстрации возможностей формулы Хэвисайда рассмотрим следующий пример: Пример 1. Найти оригинал от изображения F(s) Þ
В данном примере полином D1 выродился в полином нулевой степени, т.е. D1 = const = A. Легко видеть, что полином D0 = s2(T×S + 1) имеет полюса:
Таблица основных преобразований Лапласа.
Mетод переменных состояния.
u 1 W(s) m CAP p
Система имеет много передаточных функций: количество ТХР. Поэтому для таких многомерных систем удобно другое математическое описание.
u1(t) x 1 (t) y1(t) u2(t) x2(t) y2(t)
um(t) xn(t) yp(t)
Между «половинами» существуют внутренние переменные Обычно
где
Собственная матрица системы однозначно определяет динамические свойства системы:
первая система представляет собой систему ОДУ в обыкновенной форме Коши, вторая часть - система уравнений, описывающих выход. ОДУ в форме Коши подразумевают наличие начальных условий. В нашем случае почти всегда все элементы матрицы D будут нулевыми Þ D = 0. Такое описание системы позволяет с одной стороны стандартным образом описывать стандартные системы, используя богатое программное обеспечение, с другой стороны для простых систем, описанных в переменных «вход-выход», переход к описанию в переменных состояния зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени. Поэтому в дальнейшем мы и будем использовать подобное описание.
2.12. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода. Переход зависит от правой части:
2.12.1. Правая часть содержит только b0 u(t) Допустим, что:
Введем новую переменную х1. Первое уравнение системы:
2.12.2. Правая часть общего вида
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
где Разделим все уравнение (*) на полиномы
получим вектор переменных состояния Þ Найдем теперь регулируемую величину: Рассмотрим: Перейдем к оригиналам:
Пример: u(t) y(t) W(s) U(s) Y(s)
Необходимо свести задачу к нормальной форме Коши.
Разделим левую и правую части на
Перейдем от изображений к оригиналам:
первое матричное уравнение:
Þ Рассмотрим:
Получили второе уравнение матричной системы:
Обратная задача
Цель: Имея описание системы в переменных состояния, перейти к описанию в переменных «вход-выход». x1
x2 u y xn
um(t) yp(t) Wp,m(s)
Существует несколько алгоритмов, которые позволяют рассчитать передаточную функцию: 1. Алгоритм Фадеевой 2. 3.
индексы «3» - для 3-ей управляемой величины; «2» - по 2-му управляющему воздействию.
Пример: Имеем:
Введем переменные:
u(t) W1,1(s) y(t)º x1(t)
x1 y1(t) u(t) x2 y2(t)
По определению Т.к. Используя преобразования Лапласа, получим:
Подставим соотношения в систему уравнений Þ
Система 2-х линейной алгебраический уравнений:
Система:
Вспомогательные определители системы:
Более предпочтительно использование в знаменателе собственных чисел (см. далее). РИСУНОК
Данные графики аналогичны для случаев резонансов в теоретической механика, физике, электротехнике и т.д. Величину ω = 1 / T принято называть частотой свободных колебаний и обозначать: ω0 = 1/T В звене при β = 0 устанавливаются незатухающие колебания с частотой ω0, а само звено вырождается в консервативное. Подставляя различные значения ω в формулу (3.5.6) или (3.5.7) построим гадограф АФЧХ на комплексной плоскости:
‘легко показать’, что ω4 = 1 / T годограф консервативного звена.
Построение ЛАХ ≡ Lm(ω) не может быть сделано так просто, как для предыдущих позиционных звеньев, т.е. отрезками прямых. Будем использовать для построения графика ЛАХ нормированную (безразмерную) частоту
Введя новую переменную
Такая форма представления позволяет ‘свести’ различные ЛАХ при различных Т к автомодельному виду (‘универсальному’ виду графиков). На рис. … представлен график Lm(ω) в форме (3.5.12) построенный фактически в логарифмических координатах, причем коэффициент усиления K=1. Подчеркнем, что при такой форме представления все ЛАХ при различных T1 и T2 можно “собирать вместе”. Величина Hm (см. рис.) называется превышением:
− превышение при частоте ω = ωm Если
при ω = ωm (эта формула для “ярко выраженных” “горбов”). Вычислим переходную функцию звена h(t) =>
Найдем полюса
Для вычисления составляющей при j = 1 удобнее использовать второй вариант формулы (3.5.15) => j = 1 =>
j = 2 =>
j = 3 => Замечая много общих сомножителей в слагаемых для j = 2, 3 => суммируем составляющие при j = 2 и j = 3 =>
подставляя значения m и n =>
Величина Таким образом в описании колебательного звена появилось три “новых” частоты =>
ωm < ωc < ω0
Рассмотрим предельные случаи для β (т.е. β = 1 и β = 0) Если Если Если
− переходная функция консервативного звена =>
Если
эта формула соответствует также аналогичной формуле для апериодического звена 2- го порядка при D = 0 (совпадающие полюса).
Если
Дифференцируя во времени формулы (3.5.16 − 3.5.18) найдем соответствующие весовые (w (t)) функции: Если
Если
Если
Примерами колебательного звена можно считать:
СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ 4.1. Замена цепи из последовательно параллельно соединенных звеньев
Все реальные сист
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.230 (0.399 с.) |




 , где а – коэффициент пропорциональности (в частном случае а = Const), то такой режим управления замкнутой САУ называется режимом пропорционального управления (П-управление).
, где а – коэффициент пропорциональности (в частном случае а = Const), то такой режим управления замкнутой САУ называется режимом пропорционального управления (П-управление). , то такой режим управления называется пропорционально-инегрирующим (ПИ-управление). Þ
, то такой режим управления называется пропорционально-инегрирующим (ПИ-управление). Þ 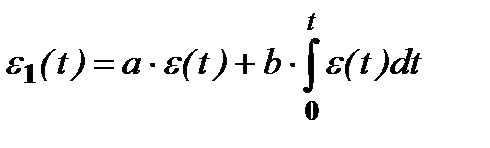 , где b – коэффициент пропорциональности (в частном случае b = Const).
, где b – коэффициент пропорциональности (в частном случае b = Const). , где c – коэффициент пропорциональности (в частном случае c = Const).
, где c – коэффициент пропорциональности (в частном случае c = Const). , то такой режим управления называется пропорционально-интегро-дифференцирующим режимом управления (ПИД-управление).
, то такой режим управления называется пропорционально-интегро-дифференцирующим режимом управления (ПИД-управление).

 c (2.5.1)
c (2.5.1) F(s) (2.5.2)
F(s) (2.5.2) , - условие сходимости, (2.5.3)
, - условие сходимости, (2.5.3)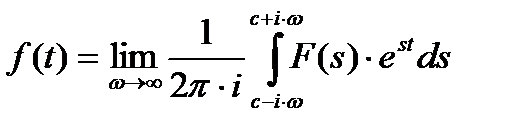 (2.5.4)
(2.5.4) (2.5.5)
(2.5.5) (2.5.6)
(2.5.6) (2.5.7)
(2.5.7) (2.5.8)
(2.5.8) Þ
Þ
 (2.5.9)
(2.5.9) (2.5.9.а)
(2.5.9.а)
 (2.5.10)
(2.5.10) (2.5.10.а)
(2.5.10.а)
 (2.5.11)
(2.5.11) ??? Þ по аналогии с предыдущим Þ
??? Þ по аналогии с предыдущим Þ
 (2.5.12)
(2.5.12) (2.5.13)
(2.5.13) Þ то Þ
Þ то Þ (2.6.1)
(2.6.1) (2.6.2)
(2.6.2) ??? Þ
??? Þ Þ
Þ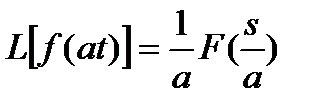 (2.6.3)
(2.6.3) - существует Þ
- существует Þ (2.6.6)
(2.6.6) (2.6.7)
(2.6.7) где D1(s) и D0(s) – полиномы по степеням «s».
где D1(s) и D0(s) – полиномы по степеням «s». , (2.7.1)
, (2.7.1) Þ
Þ  ???
???
 Þ т.е. два полюса совпадают Þ к1 = 2.
Þ т.е. два полюса совпадают Þ к1 = 2.




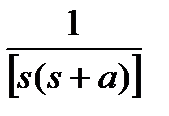

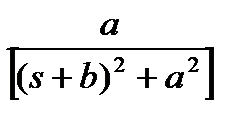


 , для каждой из которых можно записать линейное ОДУ первой степени.
, для каждой из которых можно записать линейное ОДУ первой степени. . В матричной форме эта система записывается в виде:
. В матричной форме эта система записывается в виде: ,
,
 - вектор столбец производных переменных состояния;
- вектор столбец производных переменных состояния;
 - вектор столбец переменных состояния;
- вектор столбец переменных состояния; - вектор выхода;
- вектор выхода;  - вектор входа (или вектор управления);
- вектор входа (или вектор управления);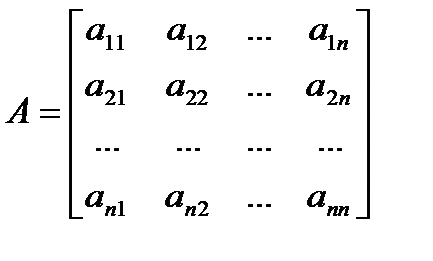 – собственная матрица системы
– собственная матрица системы  ;
; - постоянные коэффициенты;
- постоянные коэффициенты; – матрица входа
– матрица входа  ;
;  - какие-то постоянные коэффициенты;
- какие-то постоянные коэффициенты; – матрица выхода
– матрица выхода  ;
; – матрица обхода или дополнительная матрица выхода
– матрица обхода или дополнительная матрица выхода  ;
; -
-


 .
. ;
;  ;
;  ;
;  .
.
 Начальные условия нулевые.
Начальные условия нулевые.
 , (*)
, (*) ,
,  - полиномы.
- полиномы. - какая-то комплексная величина (отношение двух комплексных величин).
- какая-то комплексная величина (отношение двух комплексных величин). ,
,  - изображение какой-то переменной
- изображение какой-то переменной 
 и преобразуем:
и преобразуем:  , где
, где  - какой-то дифференциальный оператор.
- какой-то дифференциальный оператор.
 + н.у. Þ получится задача Коши Þ
+ н.у. Þ получится задача Коши Þ .
. Þ
Þ 



 н.у. нулевые.
н.у. нулевые.
 ;
; Þ
Þ


 ,
,

 - н.у.. Получаем задачу Коши для ОДУ. Þ
- н.у.. Получаем задачу Коши для ОДУ. Þ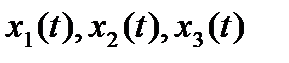 - найдены.
- найдены. ;
; .
. ;
;  ;
;  .
.
 - одно конкретное управляющее воздействие и соответствующая регулируемая величина.
- одно конкретное управляющее воздействие и соответствующая регулируемая величина.
 - алгоритм
- алгоритм - алгоритм (крайне редко пользующийся).
- алгоритм (крайне редко пользующийся). ,
, - одна и та же функция, меняющая только числитель.
- одна и та же функция, меняющая только числитель.

 ;
; 
 ,
, ,
,  ,
, Þ
Þ 






 .
. ;
;  - правило Крамера
- правило Крамера

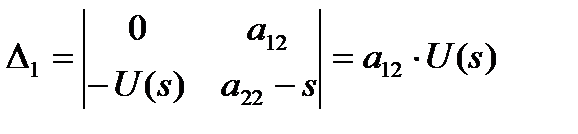




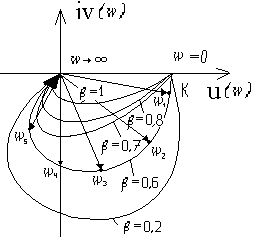
 , где ω0 − частота свободных колебаний, имеющим место в консервативном звене со следующим уравнением динамики:
, где ω0 − частота свободных колебаний, имеющим место в консервативном звене со следующим уравнением динамики: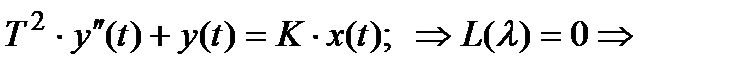


 в выражение для Lm(ω) =>
в выражение для Lm(ω) => 
 (3.5.12)
(3.5.12)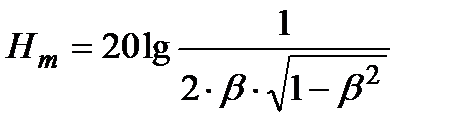 (3.5.13)
(3.5.13)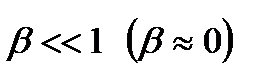 , то в упрощенных расчетах величину превышения Hm можно оценить, как:
, то в упрощенных расчетах величину превышения Hm можно оценить, как: (3.5.14)
(3.5.14)
 воспользуемся формулой Хэвисайда.
воспользуемся формулой Хэвисайда.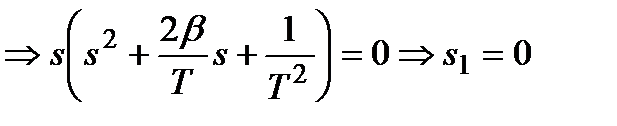
 т.к. нет повторяющихся полюсов, т.е. Kj = 1 =>
т.к. нет повторяющихся полюсов, т.е. Kj = 1 => (3.5.15)
(3.5.15)
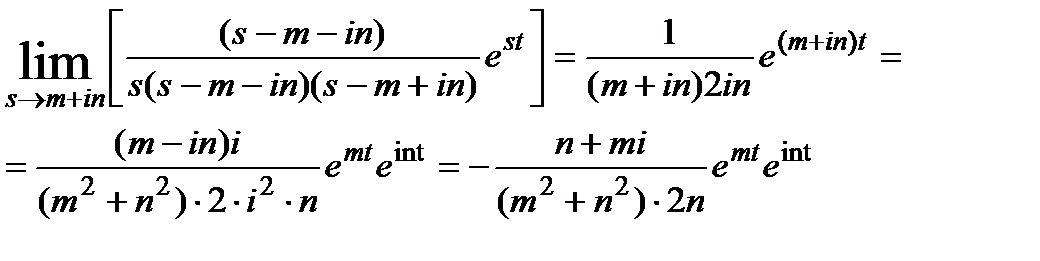




 подставляя все составляющие в формулу (3.5.15) =>
подставляя все составляющие в формулу (3.5.15) =>
 (3.5.16)
(3.5.16)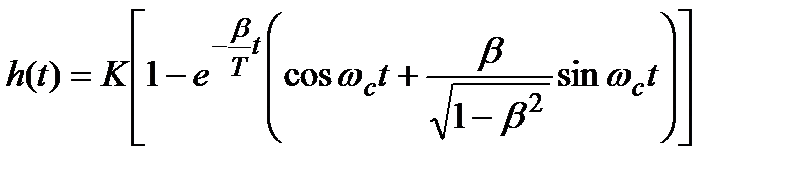 (3.5.16.а)
(3.5.16.а) называется частотой собственных колебаний (0 < β < 1).
называется частотой собственных колебаний (0 < β < 1).

 .
. т.е. собственных колебаний в звене нет, т.е. процесс без колебательный.
т.е. собственных колебаний в звене нет, т.е. процесс без колебательный.
 (3.5.17)
(3.5.17)
 возникают “трудности” со вторым слагаемым в круглых скобках формулы (3.5.16) => раскрываем неопределенность типа
возникают “трудности” со вторым слагаемым в круглых скобках формулы (3.5.16) => раскрываем неопределенность типа 

 (3.5.18)
(3.5.18)



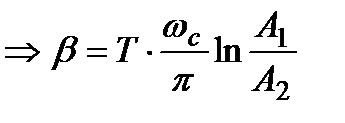 − необходимо доказать (вывести) эту формулу!!!!!
− необходимо доказать (вывести) эту формулу!!!!!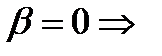
 (3.5.19)
(3.5.19)

 (3.5.20)
(3.5.20)

 (3.5.21)
(3.5.21)