
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость дифференциальных систем. ⇐ ПредыдущаяСтр 7 из 7
Рассмотрим нормальную систему обыкновенных дифф.ур.:
Где t- время, x Будем считать,что для сист.(1,32) выполняется требование сущ.единственности задачи Коши некоторой области G из про-ва Опр1. Решение
Опр2. Решение
Опр. 3 Решение Метод функции Ляпунова. Рассмотрим нормальную обыкновенную систему ДУ (1) Пусть Теорема1. (теор. Ляпунова об устойчивости) Если сущ. Функция v для которой выполняются соотношения: То нулевое решение системы (1) устойчиво. Функция удовлетворяющее условию (2) наз. функциями Ляпунова Следствие1. Если система (1) имеет автономный (стационарный, независящий от времени Теорема2 (теор. Ляпунова об асимптотический устойчивости)Если сущ. ф-ий v и w такие, что выполняются соотношения То нулевое решение системы (1) асимптотический устойчиво. Теорема3. (теор. Ляпунова о неустойчивости) Если сущ. ф-ий v и w такие,что Систему (1) вида При этом автономную линейную систему Теор4. (об устойчивости) Если линеаризация (6) асимптотически устойчива, то асимптотически устойчива и нулевое решение квазилинейной системы (5)
Следствие 2 Если вектор-ф-ия f(x) непрерывно диф-ма в окрестности т. х=0, где все характеристические числа матрицы Якоби Теор5 (о неустойчивости) Если хотя бы одно характеристическое число матрицы А имеет положительную действительную часть, то нулевое решение квазилинейной системы (5) не устойчиво.
Автономные системы. Рассмотрим автономную систему Тогда при начальном условии Это решение рассматривается как закон движения точки в пространстве При этом точка x описывает некоторую траекторию При законе движения x=x(t) вектор скорости определяется по формуле Специфика автономной системы (1) у которой в правую часть не входит время t состоит в том, что заданное поле скоростей не меняется с течением времени, т.е. является стационарным. При продолжении решения 1) решение может быть продолжено на всю полуось 2)при приближении Далее будем считать, что всегда имеет место первая ситуация. Покажем, что это ограничение не уменьшает общности. В самом деле вместе с системой (1) рассмотрим автономную систему
Поэтому можно подобрать скалярную функцию r так, чтобы скорость движения определяемая системой (2) была ограниченной. В этом случае движущаяся точка не может уйти в бесконечность за конечное время, т.е.2-ая ситуация не возможна.
Для каждой точки Вектор-функция (3) обладает следующими свойствами: 1) она непрерывна по совокупности переменных; 2) 3) Из свойства 2),3) вытекает, что при фиксированных параметрах t отображение Свойство: Если две траектории имеют общую точку, то они совпадают, а соответствующие решения отличаются лишь сдвигом по времени. Т.1: Решение x(t) системы (1) может быть только одного из следующих трёх видов: 1) непериодическое, для которого 2)периодическое для которого найдется такая постоянная T 3) постоянное, для которого Траектории соответствующие 1-му виду назыв. незамкнутыми; 2- замкнутыми; 3- точкой покоя или состоянием равновесия.
|
||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.9.141 (0.014 с.) |
 (1,32)
(1,32) ,(t,x)=(t,
,(t,x)=(t, 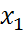 ,…,
,…, 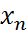 )
) .Кроме того будем считать,что все решения данной системы определены при
.Кроме того будем считать,что все решения данной системы определены при  .
.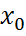 (t) системы (1,32) определенное при
(t) системы (1,32) определенное при 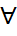 числа
числа  что все решения x(t) этой системы удовлетворяющие условию
что все решения x(t) этой системы удовлетворяющие условию  )-
)-  )
) 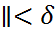 определены при
определены при  (t)
(t) 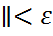
 (2.32)
(2.32) )
)  предел:
предел: (3.32)
(3.32)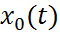 системы (1.32) наз. Неустойчивой по Ляпунову, если для некоторых
системы (1.32) наз. Неустойчивой по Ляпунову, если для некоторых  , а также для любого
, а также для любого 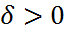 существует решение
существует решение  этой системы и сущ.момент времени
этой системы и сущ.момент времени  что имеет место неравенство:
что имеет место неравенство:  ,
,  .
.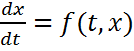 С непрерывной правой частью, определенной при
С непрерывной правой частью, определенной при  Кроме того будем считать, что система (1)имеет нулевое решение x
Кроме того будем считать, что система (1)имеет нулевое решение x 
 есть непрерывно дифференцируемые скалярные функции, положительные при х
есть непрерывно дифференцируемые скалярные функции, положительные при х  и обращаются в ноль при х=0.
и обращаются в ноль при х=0. (2)
(2) , певый интеграл v положительный в некоторой проколотой окрестности точки х=0 и v(0)=0 то нулевое решение системы (1) устойчиво.
, певый интеграл v положительный в некоторой проколотой окрестности точки х=0 и v(0)=0 то нулевое решение системы (1) устойчиво. ,
,  (3)
(3) ,
,  , будем наз. квазилинейной (системой с ведущей линейной частью) если равномерно при
, будем наз. квазилинейной (системой с ведущей линейной частью) если равномерно при 
 будем наз. линеаризацией системы (5) вдоль нулевого решения.
будем наз. линеаризацией системы (5) вдоль нулевого решения. имеют отрицательные действительные чисти, то нулевое решение автономной системы
имеют отрицательные действительные чисти, то нулевое решение автономной системы  асимптотически устойчиво.
асимптотически устойчиво.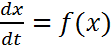 (1), где вектор-функция f(x) определена на всем пространстве
(1), где вектор-функция f(x) определена на всем пространстве  и удовлетворяет условию Липшица по всем своим аргументом в каждой ограниченной части пространства
и удовлетворяет условию Липшица по всем своим аргументом в каждой ограниченной части пространства  .
. существует и единственно решение
существует и единственно решение  системы (1) определенная в некоторой окрестности точки t=0.
системы (1) определенная в некоторой окрестности точки t=0. зависящая от выбора начальной точки
зависящая от выбора начальной точки  .
.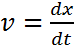 . Поэтому автономная система (1) задает поле скоростей (направлений) в фазовом пространстве
. Поэтому автономная система (1) задает поле скоростей (направлений) в фазовом пространстве  .
. вправо, т.е. в сторону возрастания t, возможны 2 ситуации:
вправо, т.е. в сторону возрастания t, возможны 2 ситуации: ;
; конечному t,
конечному t,  (т.е. решение уходит на бесконечность).
(т.е. решение уходит на бесконечность). (2), где скалярная функция
(2), где скалярная функция  и удовлетворяет тем же условиям, что и вектор-функция f(x). Эта система обладает теми же траекториями, что и система (1), отличается только скорости прохождения по эти траекториям.
и удовлетворяет тем же условиям, что и вектор-функция f(x). Эта система обладает теми же траекториями, что и система (1), отличается только скорости прохождения по эти траекториям.
 .
. пространства
пространства  при
при  ;
; (период), что
(период), что  ,а
,а  при
при  ;
;



