
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения порядка n с переменными коэффициентами
Опр. Линейным дифференциальным уравнением порядка n будем называть уравнение вида
Где функции Опр. Если в уравнении (1) функция В дальнейшем будем считать, что коэффициенты уравнения (1) и его правая часть могут принимать вообще говоря комплексные значения Опр. Комплекснозначную функцию y=f(x) будем называть решением уравнения (1) на [a;b],если она n-раз непрерывно дифференцируема на [a;b] и обращает данное уравнение в верное тождество. Непосредственным образом проверяются следующее утверждение: Лемма1 (принцип суперпозиции для уравнения (1)) Если Следствие1. Если Решение уравнения (1) всегда можно свести к решению линейной системы дифференциальных уравнений порядка n где Лемма2 Уравнение (1) эквивалентно системе (2). Доказательство осуществляется на основании замены Данная лемма позволяет перенести все результаты для линейных систем на случай линейного уравнения (1) Рассмотрим для дифференциального уравнения (1) начальные условия (3) Теорема 1 Пусть все функции Доказательство: выполним замену
В силу условий теоремы 1 матрицы А(х),F(x) –непрерывны на Согласно соответствующей теоремы для линейной системы решение задачи Коши (2),(4) существует и единственно на Поэтому и решение задачи Коши (1),(3) существует и единственно на Следствие 2 Задача Коши
Где функции
Доказательство: В самом деле тождественный нуль на Отметим, что в отличии от нелинейного уравнения теорема 1 гарантирует существование и единственность решения задачи Коши (1),(3) глобальна(т.е. на всем
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.006 с.) |
 (1)
(1)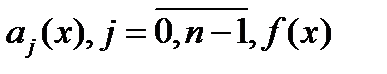 - непрерывны на отрезке [a;b], при этом известные функции
- непрерывны на отрезке [a;b], при этом известные функции 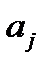 называются коэффициентами уравнения (1),а заданная функция f(x) – правой частью уравнения (1).
называются коэффициентами уравнения (1),а заданная функция f(x) – правой частью уравнения (1). на [a;b],то данное уравнение называют линейным однородным. В противном случае уравнение (1) называют неоднородным линейным.
на [a;b],то данное уравнение называют линейным однородным. В противном случае уравнение (1) называют неоднородным линейным.
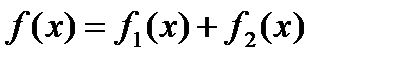 и
и  есть решение уравнения (1) при
есть решение уравнения (1) при  на [a;b],
на [a;b],  , то функция
, то функция  есть решение уравнения (1).
есть решение уравнения (1). и
и 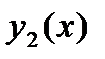 есть решения линейного однородного уравнения,
есть решения линейного однородного уравнения,  - произвольные числа (постоянные), то их линейная комбинация
- произвольные числа (постоянные), то их линейная комбинация  также является решением исходного линейного однородного уравнения.
также является решением исходного линейного однородного уравнения.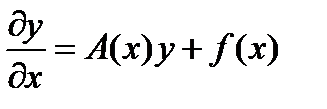 (2),
(2),
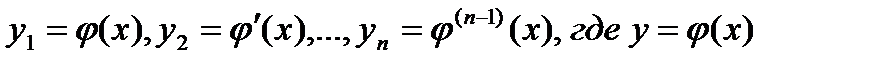 есть решение уравнения (1).
есть решение уравнения (1).
 -есть заданные числа
-есть заданные числа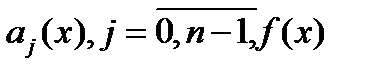 -непрерывны на
-непрерывны на  и пусть точка
и пусть точка  .Тогда при произвольных начальных значениях
.Тогда при произвольных начальных значениях  решение задачи Коши (1),(3) существует и единственно на всем отрезке
решение задачи Коши (1),(3) существует и единственно на всем отрезке  .В результате этой замены уравнение (1) сводится к системе (2).При этом начальные условия (3) примут вид
.В результате этой замены уравнение (1) сводится к системе (2).При этом начальные условия (3) примут вид (4),где
(4),где  . В силу леммы 2 задача Коши (1) и (3) эквивалентно задачи Коши (2) и (4).
. В силу леммы 2 задача Коши (1) и (3) эквивалентно задачи Коши (2) и (4).
 (5)
(5) (6)
(6)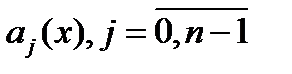 -непрерывны на
-непрерывны на 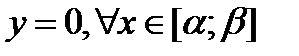 .
.



