Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выражение деформаций через напряжения
Имея в виду закон Гука
и соотношение
где n – коэффициент Пуассона, можно найти
где
Плоский случай (двухосное напряженное состояние) Многие детали машин и сооружений работают в условиях плоского напряженного состояния. Тензор напряжений при плоском напряженном состоянии условимся обозначать так
Его элементы связаны уравнениями равновесия
Элементы тензора деформаций
подчинены условию совместности
Уравнения (7.10) – (7.11) будут достаточными для решения плоской задачи, если к ним добавить еще физический закон, выражающий связь между (s) и (e). Кроме того, необходимы еще граничные условия, например, в напряжениях
где n – внешняя нормаль к границе области; рx и рy – проекции на координатные оси вектора плотности сил, приложенных к границе тела. Граничные условия (условия на поверхности) – условия равновесия элементарной призмы, вырезанной у поверхности тела. Они связывают компоненты напряжений на площадке поверхности, направляющие косинусы нормали, к которой cos(nx), cos(ny), cos(nz), с напряжениями в общем случае в трех взаимно перпендикулярных площадках в той же точке. Уравнения равновесия и условия на поверхности нужно рассматривать совместно. Уравнения равновесия без граничных условий не имеют определенного решения. Именно таким образом решалась задача о концентрации напряжений, решение которой мы рассматривали во 2-й главе; контактная задача (задача Герца), решение которой мы использовали в главе 5-й при расчете на прочность зубчатых передач. Также методами теории упругости решалась и задача о напряжениях в стенках толстостенных цилиндров (рассм. В 2.11). И многое другое. Однако, отметим, что, например, решая задачу кручения круглого стержня методом теории упругости, в котором не делается предварительных предположений о линейном распределении напряжений по радиусу, получаем те же формулы, что были выведены элементарными средствами сопротивления материалов. То же имеем и с случае чистого изгибаю Это говорит о практической целесообразности использования элементарных средств сопротивления материалов для определения напряжений и деформаций в относительно простых, и часто встречающихся на практике, случаях.
Метод конечных элементов Как уже отмечалось, еcли получение точных решений оказывается затруднительным, используются численные методы. Наиболее подходящим во многих случаях является метод конечных элементов. Этот метод универсален и его можно использовать для областей любой формы. Метод конечных элементов по существу сводится к аппроксимации сплошной среды с бесконечным числом степеней свободы совокупностью подобластей (или элементов), имеющих конечное число степеней свободы. При количественном описании технических задач инженер обычно cводит их к некоторой системе дифференциальных уравнений, справедливой в определенной области, и налагает на эту систему краевые и начальные условия. Однако точному решению поддаются пока лишь уравнения относительно простого вида. Чтобы преодолеть эти затруднения и воспользоваться машинным счетом, нужно преобразовать задачу к чисто алгебраической форме, включающей только основные арифметические операции. Для достижения этой цели используются различные виды дискретизации непрерывной задачи, определенной дифференциальными уравнениями. При этом бесконечное множество чисел, представляющих неизвестные функции, заменяется конечным числом неизвестных параметров, и для этого процесса требуется некоторая форма аппроксимации. Иначе говоря, метод конечных элементов сводится к разбиению сплошного тела на отдельные элементы, взаимодействующие между собой только в узловых точках, в которых вводятся фиктивные силы, эквивалентные поверхностным напряжениям, распределенным по границам элементов. Аппроксимация выполняется конечно-разностными уравнениями. Итак: 1. Сплошная среда разделяется воображаемыми линиями или поверхностями на некоторое число конечных элементов. 2. Предполагается, что элементы связаны между собой в узловых точках, расположенных на их границах. Основными неизвестными будут перемещения этих узловых точек. 3. Выбирается система функций, определяющая перемещения внутри каждого конечного элемента через перемещения узловых точек. 4. Функции перемещений однозначно определяют деформации внутри элемента через узловые перемещения. Эти деформации при известных начальных условиях и, например, упругих свойствах элемента позволяют определить напряжения как внутри элемента, так и на его гранях.
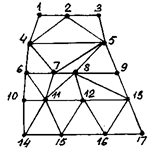
5. Определяется система сил, сосредоточенных в узлах, уравновешивающих напряжения на границе и некоторые распределенные нагрузки, а затем записываются соотношения жесткостей. Выбор формы элемента и функций перемещений для конкретных задач зависят от изобретательности, мастерства и вкуса инженера. Для примера на рис. 96 показаны треугольные конечные элементы, использованные для представления профиля плотины.
Рис. 96
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.33.153 (0.008 с.) |

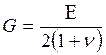 ,
,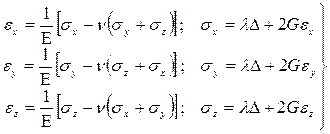 . (7.6)
. (7.6)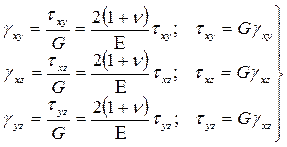 , (7.7)
, (7.7)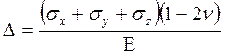 ,
, 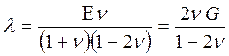 .
.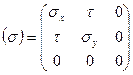 . (7.8)
. (7.8)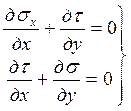 . (7.9)
. (7.9)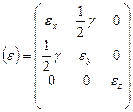
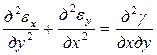 . (7.10)
. (7.10)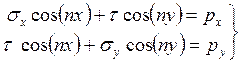 , (7.11)
, (7.11)