
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции, заданной неявно и параметрически.
Функция, заданная неявно Неявной функцией переменной Пусть дифференцируемая функция
Функция, заданная параметрически Пусть заданы две функции переменной
Задание этих функций означает задание функциональной зависимости между переменными Если в некотором интервале (a,b) функции
Тогда
Пример 4.7. Найти первую производную функции Решение Данная функция задано неявно. Продифференцируем тождество Выразим из получившегося тождества
Найдем значение первой производной в в точке
Пример 4.8. Найти первую и вторую производные функции Решение: Данная функция задано неявно. Продифференцируем тождество
Выразим из получившегося тождества
Из условия имеем
Найдем вторую производную, продифференцировав получившееся равенство по переменной x, имея в виду, что
Итак, имеем
Пример 4.9. Написать уравнение касательной и уравнение нормали к линии Решение
Нам необходимо написать уравнение касательной в точке Найдем производную, продифференцировав тождество
Разделим получившееся тождество на ln 2 и подставим вместо
Напишем уравнение касательной:
Напишем уравнение нормали:
Итак.
Пример 4.10. Найти первую и вторую производные функции, заданной параметрически: 1) Решение 1) Первую производную функции, заданной параметрически, найдем по формуле: Найдем производные функций Тогда
Вторую производную функции, заданной параметрически, найдем по формуле: Продифференцируем функцию
Тогда Таким образом:
2) Первую производную функции, заданной параметрически, найдем по формуле: Найдем производные функций
Тогда
Вторую производную функции, заданной параметрически, найдем по формуле: Продифференцируем функцию
Тогда Таким образом:
Пример 4.11. Написать уравнение касательной и уравнение нормали к кривой Решение
Найдем значение функции
Следовательно, Найдем значение функции
Следовательно, Вычислим производную функции по формуле Для этого найдем производные функций
Тогда по формуле
Следовательно, Напишем уравнение касательной:
Напишем уравнение нормали:
Итак.,
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.43.140 (0.025 с.) |
 называется функция, значения которой находятся из уравнения, связывающего
называется функция, значения которой находятся из уравнения, связывающего  , и не разрешенного относительно
, и не разрешенного относительно 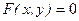 . Тогда производную
. Тогда производную  можно найти, дифференцируя тождество
можно найти, дифференцируя тождество  Производная функции, заданной неявно выражается через переменную
Производная функции, заданной неявно выражается через переменную 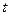 :
: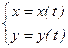 .
.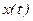 и
и 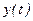 дифференцируемы и
дифференцируемы и 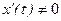 , то на интервале (a,b) функция
, то на интервале (a,b) функция 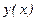 однозначно определена, дифференцируема и
однозначно определена, дифференцируема и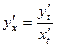 .
.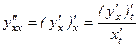
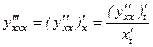 и т.д.
и т.д.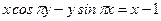 в точке
в точке 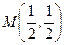 .
.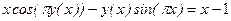 по переменной x, имея в виду, что
по переменной x, имея в виду, что 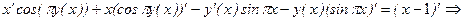
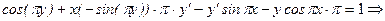
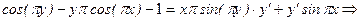
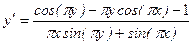 .
.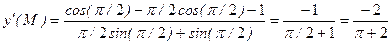
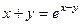 .
.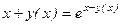 по переменной x, имея в виду, что
по переменной x, имея в виду, что 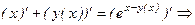
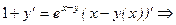
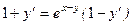 .
.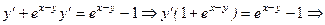
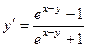 .
.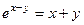 ; тогда
; тогда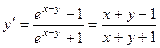 .
.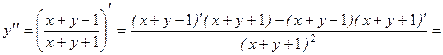
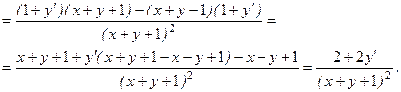
 Выражение для
Выражение для 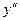 и получим:
и получим: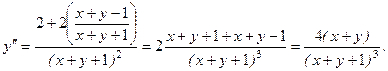
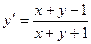 ;
;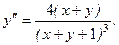
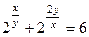 в точке
в точке 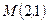 .
.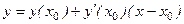 -уравнение касательной в точке
-уравнение касательной в точке  ;
;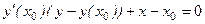 - уравнение нормали в точке
- уравнение нормали в точке  ; а
; а  .
.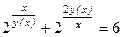 по переменной x, имея в виду, что
по переменной x, имея в виду, что 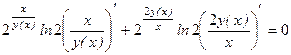 ;
;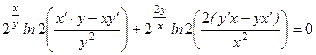 ;
;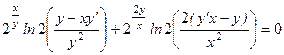 .
.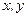 координаты точки М(
координаты точки М(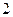 ;
; 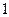 ), а затем найдем производную функции в точке М:
), а затем найдем производную функции в точке М: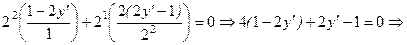
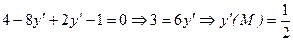 .
.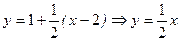 .
.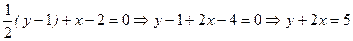 .
.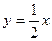 - уравнение касательной в точке М(2.1);
- уравнение касательной в точке М(2.1);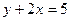 - уравнение нормали в точке М(2.1).
- уравнение нормали в точке М(2.1).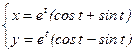 ; 2)
; 2) 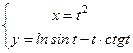 .
.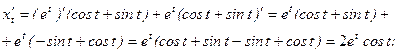
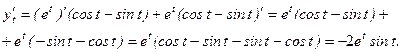
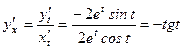 .
.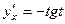 по переменной
по переменной 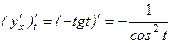 .
.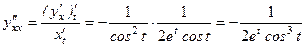 .
.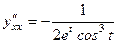 .
.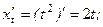
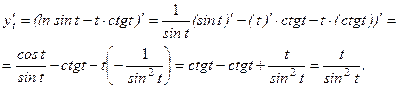
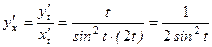 .
.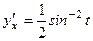 по переменной
по переменной 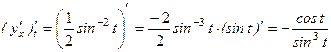 .
.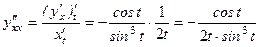 .
.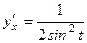 ;
;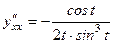
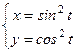 в точке, соответствующей значению параметра
в точке, соответствующей значению параметра 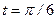 .
.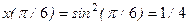 .
.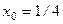
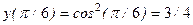 .
.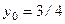
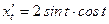 ;
;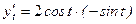
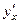 :
: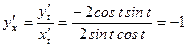 .
.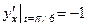 .
.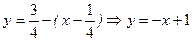 .
.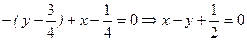 .
.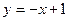 - уравнение касательной в точке М(2.1);
- уравнение касательной в точке М(2.1);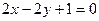 - уравнение нормали в точке М(2.1).
- уравнение нормали в точке М(2.1).


