
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідження графіка функції на опуклість, угнутість.
Точки перегину Нехайкрива, що задана рівнянням y=f(x), гладка на деякому інтервалі (a;b), тобто функція f(x) неперервна і неперервно диференційовна на цьому інтервалі. Тоді в кожній точці такої кривої можна провести дотичну. Означення. Крива називається опуклою(угнутою) на інтервалі (a;b), якщо всі її точки, крім точки дотику, лежать під (над) довільною її дотичною на цьому інтервалі (рис.10 – крива опукла на інтервалі (a;b); рис.11 – крива угнута на інтервалі (a;b)).
Приклади 1. Півколо 3. Парабола 4. Кубічна парабола
Установлення інтервалів, де крива опукла, угнута, та знаходження точок перегину має важливе значення для характеристики поведінки функції f(x). Дослідження на опуклість, угнутість і перегин кривої аналогічне дослідженню на монотонність та екстремум функції, при умові, що за функцію приймаємо Ознака опуклості та вгнутості кривої: нехай функція f(x) двічі диференційовна на (a;b). Тоді, якщо для будь-якого
якщо Для того щоб легше запам’ятати зв'язок між знаком другої похідної і поведінкою кривої, можна скористатися уже згадуваним раніше мнемонічним «правилом ковшика», його ще називають «правилом дощу»: дощ, падаючи на графік функції, розсіюється на випуклих ділянках, на яких
Самі ж точки В та С суть точки перегину. Означення. Інтервалами опуклості, угнутості кривої називаються інтервали її області визначення, в яких крива або лише опукла, або лише угнута. Із наведеної вище ознаки ясно, що в інтервалах опуклості, угнутості кривої друга похідна зберігає знак, тобто ці інтервали є інтервалами знакосталості другої похідної. Проводячи далі аналогію з дослідженням функції на екстремум, приходимо висновку, що абсциси точок перегину є точками екстремуму першої похідної Необхідна ознака існування точки перегину: якщо Означення. Критичними точками 2-го роду функції f(x) називаються точки її області визначення, в яких друга похідна Критичні точки 2-го роду розбивають ОВФ на інтервали опуклості та угнутості. Сформульована вище необхідна ознака не є достатньою для існування точки перегину. Абсциси точок перегину слід шукати серед критичних точок 2-го роду. Проте не всяка критична точка 2-го роду є абсцисою точки перегину. Наприклад, крива Достатня ознака існування точки перегину: якщо при переході через критичну точку 2-го роду Правило дослідження кривої y=f(x) на опуклість, угнутість, перегин:
Приклад. Знайти інтервали опуклості, угнутості та точки перегину кривої
Розв’язання. 1) ОВФ – вся числова вісь. 2) 3) Знаходимо критичні точки 2-го роду:
5) Визначаємо знак похідної на кожному з цих інтервалів: а) б) в) 6) Оскільки при переході через критичну точку 7) Знаходимо координати точки перегину:
Точка перегину має координати P(-1;3).
Асимптоти кривої При дослідженні функції і побудові її графіка важливо вияснити характер її поведінки в околі точок розриву і точок, де функція не визначена, а також вияснити її поведінку при
наближення – асимптотичним. З поняттям асимптоти ми вперше зустрілись в курсі аналітичної геометрії при дослідженні форми гіперболи. Узагальнимо це поняття на довільні криві. Означення. Пряма називається асимптотою кривої, якщо відстань від біжучої точки М кривої до цієї прямої прямує до нуля, коли точка М рухається по кривій в нескінченність. Крива може наближатися до своєї асимптоти тими ж способами, що і змінна до своєї границі, залишаючись з однієї сторони від асимптоти або з різних сторін, нескінченне число разів перетинаючи асимптоту і переходячи з однієї її сторони на другу (дивись рис. 20, 21, 22). Розрізняють три види асимптот: вертикальні, горизонтальні та похилі. Найпростіше знайти асимптоти, паралельні осям координат, – вертикальні та горизонтальні. Вертикальна асимптота паралельна осі Oy. Рівняння вертикальної асимптоти кривої y=f(x) має вигляд x=a, де a – значення аргументу, при якому функція f(x) обертається на нескінченність (терпить нескінченний розрив – дивись рис. 20). Інакше кажучи, для того щоб пряма x=a була вертикальною асимптотою кривої y=f(x), необхідно і достатньо виконання хоча б однієї із умов
Таким чином, вертикальні асимптоти можуть бути або в точках нескінченних розривів функції, або на межах ОВФ. Причому границі знаходять ліворуч та праворуч від точки розриву. Для знаходження вертикальних асимптот потрібно знайти ті скінченні значення аргументу, при яких функція необмежено зростає за абсолютною величиною. Додаткову інформацію відносно поведінки кривої при
Горизонтальна асимптота паралельна осі Ox. Пряма y=b є горизонтальною асимптотою кривої y=f(x), якщо існує границя
При
Похилі асимптоти. Питання про існування похилих асимптот вирішується за допомогою наступної теореми. ТЕОРЕМА. Для того щоб пряма
(відповідно При Коментарі до теореми. 1. Якщо хоча б однієї із границь у кожному випадку (3) та (4) не існує, то крива y=f(x) похилих асимптот не має. 2. Горизонтальну асимптоту можна розглядати як частинний випадок похилої асимптоти при Цілком можливо, що одна із віток графіка функції має похилу асимптоту, а друга – ні, або ж кожна із віток має свою похилу асимптоту. Коли крива монотонно наближається до асимптоти, то слід постаратися вияснити (якщо це не важко), з якого боку від цієї асимптоти знаходиться крива. Для дослідження розміщення кривої відносно асимптоти потрібно окремо розглядати випадки, коли Знання асимптот значно полегшує побудову графіка функції і дає повне уявлення про його поводження в нескінченності. Більше того, знаючи асимптоти (особливо коли є вертикальні і похилі), можна зробити ескіз графіка функції. Приклад 1. Знайти асимптоти графіка функції Розв’язання. 1) ОВФ: При При
Знаючи поведінку функції в околі точки розриву x =1, можна уже побудувати «кусок» графіка функції (дивись рис. 24)
3) Горизонтальні асимптоти. Оскільки існує границя 4) Залишилось з’ясувати питання про існування похилих асимптот
Знову дістали рівняння горизонтальної асимптоти y =1 (як частинний випадок похилої при k =0).
Визначимо знак різниці
Здобута інформація дає змогу, доповнивши рис. 24, побудувати ескіз графіка даної функції (рис. 25).
Приклад 2. Знайти асимптоти графіка функції Розв’язання. 1) ОВФ:
А це означає, що графік функції Приклад 3. Знайти асимптоти кривої Розв’язання. 1) ОВФ: 2) Вертикальні асимптоти. Крива має вертикальну асимптоту x=0, так як x=0 – це точка розриву 2-го роду. Дійсно, знайдемо границі:
Пряма 3) Горизонтальних асимптот крива не має, оскільки
4) Похилі асимптоти
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 959; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.45.162 (0.06 с.) |
 Означення. Точкою перегину називається така точка неперервної кривої, яка відділяє її опуклу частину від угнутої (рис.12,13;
Означення. Точкою перегину називається така точка неперервної кривої, яка відділяє її опуклу частину від угнутої (рис.12,13; 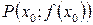 – точка перегину кривої).
– точка перегину кривої). – це крива, яка опукла на інтервалі (-1;1) (рис. 14). 2. Крива, задана рівнянням
– це крива, яка опукла на інтервалі (-1;1) (рис. 14). 2. Крива, задана рівнянням  (показникові функція) угнута на інтервалі
(показникові функція) угнута на інтервалі  (рис. 15).
(рис. 15). також угнута на всій числовій осі (рис. 16).
також угнута на всій числовій осі (рис. 16). має точку перегину (0;0), яка розмежовує опуклу і угнуту частини її графіка (рис. 17).
має точку перегину (0;0), яка розмежовує опуклу і угнуту частини її графіка (рис. 17). Не всяка крива має точки перегину. Криві, зображені на рис. 14, 15, 16, точок перегину не мають. Іноді крива може мати їх декілька або, як синусоїда, навіть нескінченну множину.
Не всяка крива має точки перегину. Криві, зображені на рис. 14, 15, 16, точок перегину не мають. Іноді крива може мати їх декілька або, як синусоїда, навіть нескінченну множину. , а за її похідну –
, а за її похідну –  Аналогічно тому, як за знаком першої можна визначити, зростає чи спадає функція, так за знаком другої похідної можна зробити висновок, в яку сторону вигинається лінія графіка функції. Іншими словами, аналізуючи знак другої похідної, можна встановити, на яких інтервалах крива опукла, а на яких угнута. При цьому, інтервалу спадання першої похідної відповідає інтервал опуклості графіка функції, а інтервалу зростання – інтервал угнутості.
Аналогічно тому, як за знаком першої можна визначити, зростає чи спадає функція, так за знаком другої похідної можна зробити висновок, в яку сторону вигинається лінія графіка функції. Іншими словами, аналізуючи знак другої похідної, можна встановити, на яких інтервалах крива опукла, а на яких угнута. При цьому, інтервалу спадання першої похідної відповідає інтервал опуклості графіка функції, а інтервалу зростання – інтервал угнутості.
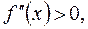 то крива угнута на (a;b);
то крива угнута на (a;b); , то крива опукла на (a;b).
, то крива опукла на (a;b). і збирається на угнутих, на яких
і збирається на угнутих, на яких  (дивись рис. 18). Схематично це можна зобразити ще й так:
(дивись рис. 18). Схематично це можна зобразити ще й так:  , де знаки нерівностей суть: V – угнутість;
, де знаки нерівностей суть: V – угнутість;  –опуклість.
–опуклість. На рис. 18 крива y=f(x) випукла на ділянках АВ і СД і угнута на ділянці ВС. Рис. 18.
На рис. 18 крива y=f(x) випукла на ділянках АВ і СД і угнута на ділянці ВС. Рис. 18.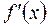 і для знаходження цих точок можна скористатися необхідною і достатньою ознаками екстремуму.
і для знаходження цих точок можна скористатися необхідною і достатньою ознаками екстремуму.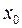 – абсциса точки перегину, то
– абсциса точки перегину, то  або
або  або
або  не існує.
не існує. дорівнює нулю або дорівнює нескінченності або ж не існує.
дорівнює нулю або дорівнює нескінченності або ж не існує. має другу похідну
має другу похідну  яка при
яка при  дорівнює нулю
дорівнює нулю 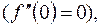 але
але 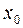 функції
функції  друга похідна
друга похідна 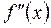 змінює знак, то точка
змінює знак, то точка 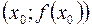 є точкою перегину цієї кривої.
є точкою перегину цієї кривої.

 ;
;
 – критичні точки 2-го роду.
– критичні точки 2-го роду.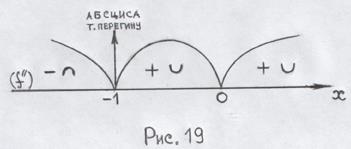 4) Відмічаємо критичні точки на ОВФ. Інтервали опуклості, угнутості:
4) Відмічаємо критичні точки на ОВФ. Інтервали опуклості, угнутості: 
 – крива опукла на інтервалі
– крива опукла на інтервалі  ;
; – крива угнута на інтервалі (-1;0);
– крива угнута на інтервалі (-1;0); – крива угнута на інтервалі
– крива угнута на інтервалі 
 друга похідна змінює знак, то точка
друга похідна змінює знак, то точка  є абсцисою точки перегину. При переході через критичну точку
є абсцисою точки перегину. При переході через критичну точку  друга похідна не змінює знак, тому ця точка не є абсцисою точки перегину.
друга похідна не змінює знак, тому ця точка не є абсцисою точки перегину.
 та
та  . Інакше кажучи, важливо установити форму графіка функції при віддаленні його змінної (біжучої) точки М в нескінченність. Якщо при цьому графік функції необмежено наближається до деякої прямої, то цю пряму називають асимптотою кривої, а саме
. Інакше кажучи, важливо установити форму графіка функції при віддаленні його змінної (біжучої) точки М в нескінченність. Якщо при цьому графік функції необмежено наближається до деякої прямої, то цю пряму називають асимптотою кривої, а саме
 або
або  або
або  (1)
(1) можна дістати, якщо установити до чого прямує при цьому функція
можна дістати, якщо установити до чого прямує при цьому функція  до
до 
 чи до
чи до  . Рис. 23 ілюструє всі можливі випадки (а їх чотири) поведінки функції f(x) при
. Рис. 23 ілюструє всі можливі випадки (а їх чотири) поведінки функції f(x) при  , де x=a – точка розриву 2-го роду.
, де x=a – точка розриву 2-го роду.
 або
або  . (2)
. (2) асимптота називається правою горизонтальною, а при
асимптота називається правою горизонтальною, а при  була похилою асимптотою графіка функції f(x) при
була похилою асимптотою графіка функції f(x) при  необхідно і достатньо існування границь
необхідно і достатньо існування границь
 (3)
(3)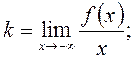
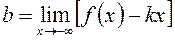 ) (4)
) (4) асимптота називається правою похилою, а при
асимптота називається правою похилою, а при  .
. та
та  і в кожному із цих випадків визначати знак різниці
і в кожному із цих випадків визначати знак різниці  Якщо він буде додатним, то крива розміщена над асимптотою, а якщо від’ємним, то під асимптотою. Коли ж ця різниця не буде знакосталою, то крива буде коливатися біля своєї асимптоти.
Якщо він буде додатним, то крива розміщена над асимптотою, а якщо від’ємним, то під асимптотою. Коли ж ця різниця не буде знакосталою, то крива буде коливатися біля своєї асимптоти. .
. – вся числова вісь, крім точки розриву x =1. 2) Вертикальною асимптотою може бути лише пряма x =1, так як точка x =1 є точкою розриву 2-го роду. Знайдемо границі
– вся числова вісь, крім точки розриву x =1. 2) Вертикальною асимптотою може бути лише пряма x =1, так як точка x =1 є точкою розриву 2-го роду. Знайдемо границі  та
та 
 (x наближається до 1 зліва) чисельник прямує до 1, а знаменник, пряму до нуля, залишається весь час від’ємним і тому значення функції прямують до
(x наближається до 1 зліва) чисельник прямує до 1, а знаменник, пряму до нуля, залишається весь час від’ємним і тому значення функції прямують до 
 (x наближається до 1 справа) чисельник прямує до 1, а знаменник, прямуючи до нуля, залишається весь час додатним. В свою чергу, значення функції прямують до
(x наближається до 1 справа) чисельник прямує до 1, а знаменник, прямуючи до нуля, залишається весь час додатним. В свою чергу, значення функції прямують до 

 Отже, пряма x =1 є вертикальною асимптотою графіка функції.
Отже, пряма x =1 є вертикальною асимптотою графіка функції. то пряма y =1 є горизонтальною асимптотою графіка функції.
то пряма y =1 є горизонтальною асимптотою графіка функції. Для цього обчислимо
Для цього обчислимо

 при
при  та
та 

 при
при 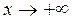 – крива розміщена над асимптотою;
– крива розміщена над асимптотою;
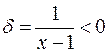 при
при 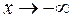 – крива розміщена під асимптотою.
– крива розміщена під асимптотою.
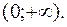 2) Вертикальні асимптоти. При підході до граничної точки x =0 функція необмежено спадає:
2) Вертикальні асимптоти. При підході до граничної точки x =0 функція необмежено спадає: Отже, пряма x =0 (вісь ординат) є вертикальною асимптотою графіка цієї функції. 3) Горизонтальні асимптоти.
Отже, пряма x =0 (вісь ординат) є вертикальною асимптотою графіка цієї функції. 3) Горизонтальні асимптоти.  Оскільки
Оскільки  то горизонтальних асимптот графік функції не має. 4) Похилі асимптоти
то горизонтальних асимптот графік функції не має. 4) Похилі асимптоти  шукаємо тільки при
шукаємо тільки при  .
.

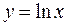 не має похилих асимптот (рис. 26).
не має похилих асимптот (рис. 26).
 Функція визначена на всій числовій осі Ox, крім точки x =0, де вона розривна.
Функція визначена на всій числовій осі Ox, крім точки x =0, де вона розривна.


 – вертикальна асимптота даної кривої.
– вертикальна асимптота даної кривої.

 де
де 

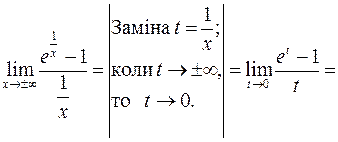
 .
. Пряма
Пряма  – похила асимптота даної кривої. Графік функції
– похила асимптота даної кривої. Графік функції  схематично показаний на рис. 27.
схематично показаний на рис. 27.


