
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. Комплексні числа (к. ч.)Стр 1 из 3Следующая ⇒
IV. Комплексні числа (к. ч.) Дійсні числа Нагадаємо, що числа 1, 2, 3, 4,..., n,..., за допомогою яких ведеться лічба, називаються натуральними. Множину натуральних чисел прийнято позначати буквою N,
Якщо до множини натуральних чисел включити число нуль, а також –1, –2, –3,..., то утвориться множина цілих чисел Z ={..., –3, – 2, –1, 0, 1, 2, 3,...}. Раціональні – це числа вигляду Числа, які виражаються нескінченними неперіодичними десятковими дробами називаються ірраціональними (нераціональними). Множину ірраціональних чисел позначають буквою І. Прикладами ірраціональних чисел є:
Об’єднання множин раціональних і ірраціональних чисел утворює множину дійсних чисел (позначається буквою R), тобто:
Відомо, що між точками числової осі ОХ і множиною дійсних чисел R існує взаємно однозначна відповідність.
Квадратні рівняння з від’ємними дискримінантами Відомо, що корені квадратного рівняння
знаходяться за формулами
де вираз При D >0 корені квадратного рівняння дійсні і різні; при D =0 корені дійсні і рівні; при D <0 говорять. що дійсні корені не існують, а існують, так звані, комплексні корені. Приклад. Знайти корені квадратного рівняння
За формулами (2) маємо:
Серед дійсних чисел вираз Символ
його називають уявною одиницею. Тепер корені рівняння
Перевірка. Для
Аналогічно робиться перевірка для Отже, для квадратного рівняння
Приклади для самостійного розв’язання Розв’язати квадратні рівняння: 1. 3. 5. 7. 9. Відповіді. 1.
Алгебраїчна форма к.ч. В алгебраїчній формі к.ч.мають вигляд
Два к.ч. називаються рівними, якщо відповідно рівні їх дійсні та уявні частини. Основні операції над к.ч. в алгебраїчній формі введені в §§4.4,4.5,4.6. Надалі домовимось вирази Нехай дано число Приклад. Розв’язати рівняння Розв¢язання. З рівності к.ч. випливає:
Спряжені к.ч.
Числа Очевидно, якщо Приклади. 1) Якщо 2) Безпосередньо перевіряється тотожність
Модуль к.ч.
Модулем числа Модуль дійсного числа дорівнює його абсолютній величині. Справді, якщо Приклади. 1) 2) 3) 4) Показати, що модулі спряжених чисел рівні. Розв¢язання. Досить обчислити модулі спряжених чисел
Додавання і віднімання к.ч.
Приклади 1. 2. Обчислити самостійно 1. 3. 5. 7. 9. Відповіді. 1. 8.
Множення к.ч.
Множення к.ч. виконуємо згідно правила (вважаючи, що
Приклади.
Правильна тотожність
Спростити самостійно 1. 3. 5. 7. Відповіді. 1. 6.
Ділення к.ч.
Ділення к.ч. виконується згідно правила (при умові
Приклади. 1)
2) 3) Розв’язати рівняння Розв’язання. Перевірка:
Спростити самостійно вирази 1. Відповіді. 1.
Коло, круг, кільце Нехай дано числа Рівнянню Очевидно, що нерівності Звернемо увагу на вироджені випадки кільця
(1) (2) (3) (4) при
Рис. 1.2
Приклад. З’ясувати, чи належить точка Розв’язання. Порівняємо радіус
Відповідь: точка
Комплексне число як вектор
Кожному к.ч. Якщо вектор Нехай
Рис.1.3 Очевидно,
Множення і ділення к.ч.в геометричній формі розглядаються в §1.14. Приклад. Доведемо нерівність Використовуємо простий факт: сума довжин довільних двох сторін трикутника більша довжини третьої сторони. З рис. 1.3 випливає, що Випадок чисел, розміщених на одній прямій пропонуємо розглянути самостійно. Приклад. Знайти суму і різницю Розв’язання.
Виконати самостійно В умовах попереднього прикладу знайти 2)
Кут нахилу вектора до осі
Розглянемо довільний ненульовий вектор
Рис. 1.4 Таким чином, кут нахилу задає напрямок вектора. З рис.1.4. випливає, що додатний j+ і від’ємний j- кути визначають один і той же напрямок. Очевидно також, якщо довільний кут j задає деякий напрямок, то такий же напрямок будуть задавати і кути Приклад. Легко перевірити, що кути 1350,4950,-2250,-9450 визначають один і той же напрямок (відносно осі
Аргумент комплексного числа Нехай вектор
Таким чином, аргумент к.ч. набуває нескінченну множину значень. Аргумент числа
Рис. 1.5 Найменше за абсолютною величиною значення Приклади. 1) Використовуючи рис. 1.6, легко переконатись, що
Рис. 1.6 2) Для довільного
Обчислення аргументу Спочатку відмітимо властивість: 1) Аргумент дійсного і чисто уявного числа: якщо 2) Аргумент будь-якого числа
Доведемо останню формулу у випадку, коли
Рис 1.7
Інші випадки розміщення числа Зауважимо, що вказаним способом для аргументу можна одержати формули, в яких використовуються арккотангенс, арккосинус чи арксинус. Якщо не вимагається високої точності, то аргумент к.ч. можна знаходити графічно. З цією метою слід побудувати к.ч. на міліметровому папері і виміряти відповідний кут за допомогою транспортиру. Цей спосіб іноді використовують для грубої перевірки обчислень. Приклад 1. Покажемо, як обчислюють аргументи чисел
Приклад 2. Достатньо встановити знаки дійсної і уявної частин к.ч., щоб перевірити рівності:
Tpигонометрична форма к.ч.
Нехай відомі модуль У випадку розміщення осей
Остання форма запису комплексного числа називається тригонометричною. Як бачимо, щоб знайти тригонометричну форму, досить обчислити модуль і аргумент к.ч. Приклади. Записати в тригонометричній формі слідуючі числа: 1) Розв’язання 1) Відповідь: 2) Відповідь: 3) Відповідь: Розглянемо алгоритм переходу від алгебраїчної до тригонометричної форми к.ч. Нехай дано к.ч. 1. Побудувати на площині ХОУ к.ч.
2. Знаходимо модуль к.ч.
На прикладі маємо:
3. За допомогою таблиць або мікрокалькулятора знаходимо
На прикладі: 4. За формулою (1.1) § 1.14 знаходимо
5. Підставимо знайдені
Для
Відповіді. 1. 1) 2) 3) 2. 1) 2) 3)
4.17. Формула піднесення к.ч.до цілого степеня n
(Формула Муавра): якщо
Приклад. Нехай Розв’язання. Подамо
Формула добування коренів
Формула добування коренів
де Таким чином, Приклад. Знайти всі значення Розв’язання. Запишемо число 8 в тригонометричній формі:
Одержуємо три значення кореня:
Формула Ейлера Формула Ейлера має вигляд:
де Зміст цієї рівності в тому, що вона визначає експоненту (за основою За допомогою формул §§4.14,4.15,4.3 (приклад 3) безпосередньо перевіряються слідуючі властивості:
Приклад. Обчислити Розв’язання.
4.20. Експонента ez Нехай Основні властивості:
Для доведення використовуються властивості експоненти з дійсними і чисто уявними показниками (див.§1.17). Приклад 1. Знайти Розв’язання. Якщо Відповідь: Приклад 2. Обчислити Розв’язання. Приклад 3. Показати, що якщо Розв’язання. Нехай Залишилось зауважити, що границя змінної величини дорівнює нулю тоді і тільки тоді, коли границя її модуля дорівнює нулю. Показникова форма к.ч.
Нехай
Така форма запису чисел дозволяє використовувати властивості експоненти і тому зручна для різних перетворень. Множення, ділення і піднесення до степеня к.ч.: якщо
Приклад 1. Записати у показниковій формі к.ч. Розв’язання. Користуємось алгоритмом, який вже викладений у §1.15. 1. Будуємо к.ч.
З рис. видно, що 2. Обчислюємо модуль к.ч.
3. Знаходимо 4. Оскільки
5. За формулою
Перевірка.
Відповідь. Приклад 2. Використовуючи показникову форму чисел Розв’язання. Знаходимо квадрати модулів і аргументи
Виконуючи дії над числами в показниковій формі, отримаємо До алгебраїчної форми запису числа
Відповіді. 1. 3.
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.28.48 (0.303 с.) |
 = {1, 2, 3, …, n,...}.
= {1, 2, 3, …, n,...}. , де q – натуральне, а p – ціле. Множина раціональних чисел позначається Q = {
, де q – натуральне, а p – ціле. Множина раціональних чисел позначається Q = {  }. Раціональні числа
}. Раціональні числа 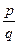 – виражаються звичайними дробами, які можна перетворювати у десяткові: скінченні або нескінченні періодичні.
– виражаються звичайними дробами, які можна перетворювати у десяткові: скінченні або нескінченні періодичні. =3,1415926536897931..., е = 2,71828182845904535...,
=3,1415926536897931..., е = 2,71828182845904535..., = 1,4142135623..., і т.п.
= 1,4142135623..., і т.п.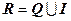 .
. (1)
(1) (2)
(2) називають дискримінантом.
називають дискримінантом.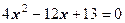 .
. .
.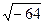 не має смислу, тобто
не має смислу, тобто  .
. прийнято позначати буквою і, тобто:
прийнято позначати буквою і, тобто: , а
, а 
 .
. маємо:
маємо:
 .
. .
. і
і 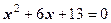 2.
2. 
 4.
4. 
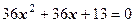 6.
6. 
 8.
8. 
 10.
10. 
 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5. 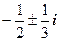 . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  .
. , де
, де  дійсні числа; число
дійсні числа; число  називається дійсною, а
називається дійсною, а  – уявною частиною к.ч.; позначення:
– уявною частиною к.ч.; позначення:  ; символ
; символ 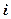 формально визначається рівністю
формально визначається рівністю 
 і т.п. вважати к.ч., записаними в алгебраїчній формі, отже,
і т.п. вважати к.ч., записаними в алгебраїчній формі, отже,  і т.п. набуватимуть тільки дійсних значеннь.
і т.п. набуватимуть тільки дійсних значеннь. , то
, то  дійсне число:
дійсне число: 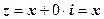 ; якщо
; якщо 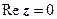 , то
, то  називається чисто уявним числом:
називається чисто уявним числом:  .
. ; де
; де  дійсні числа.
дійсні числа.
 . Розв’язуючи цю систему, одержимо
. Розв’язуючи цю систему, одержимо  .
. називаються спряженими. Таким чином, якщо
називаються спряженими. Таким чином, якщо  і
і  – спряжені числа, то
– спряжені числа, то  і
і  .
. дійсне число, то
дійсне число, то  ; якщо
; якщо  – чисто уявне число, то
– чисто уявне число, то  . Навпаки, якщо
. Навпаки, якщо 
 , то
, то  .
.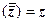 .
. називається невід’ємне число
називається невід’ємне число  .
. , то
, то  .
. .
.
 .
.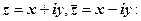



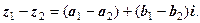
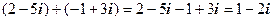 .
. .
. 2.
2. 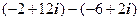
 4.
4. 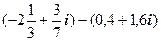
 6.
6. 
 8.
8. 
 10.
10. 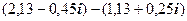
 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7. 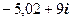 .
. . 9.
. 9.  . 10.
. 10.  .
.


 .
.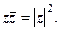

 2.
2. 
 4.
4. 
 6.
6. 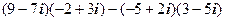

 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
. . 7.
. 7.  .
.  ):
):





 Відповідь:
Відповідь: 
 2.
2.  3.
3.  .
. . 3.
. 3.  .
.
 задовольняють всі числа (і тільки вони), що розміщені на колі радіуса
задовольняють всі числа (і тільки вони), що розміщені на колі радіуса  з центром у точці
з центром у точці  . Дійсно, якщо
. Дійсно, якщо 
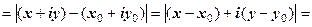
 .
. і
і  задають відповідно круг і кільце. На рис. 1.2 зображено кільце
задають відповідно круг і кільце. На рис. 1.2 зображено кільце  з центром у точці
з центром у точці  .
. – круг з виключеним центром
– круг з виключеним центром 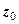 ;
; – зовнішність круга
– зовнішність круга  – круг з границею;
– круг з границею; – вся площина з виключеною точкою
– вся площина з виключеною точкою  маємо пусту множину.
маємо пусту множину.
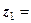 p до круга
p до круга  .
. з відстанню
з відстанню  від центра круга
від центра круга 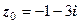 до точки
до точки  .
. , і навпаки, кожному радіусу-вектору
, і навпаки, кожному радіусу-вектору 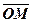 або довільним направленим відрізком, який при паралельному переносі збігається з
або довільним направленим відрізком, який при паралельному переносі збігається з  зображає к.ч.
зображає к.ч. 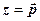 .
. Розглянемо паралелограм
Розглянемо паралелограм  , див. рис.1.3.
, див. рис.1.3.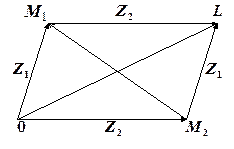

 , тобто сума і різниця к.ч. відповідають сумі і різниці векторів. Таким чином, додавання і віднімання набуває простого геометричного змісту.
, тобто сума і різниця к.ч. відповідають сумі і різниці векторів. Таким чином, додавання і віднімання набуває простого геометричного змісту. , яка є узагальненням нерівності абсолютних величин дійсних чисел.
, яка є узагальненням нерівності абсолютних величин дійсних чисел. , тобто
, тобто  .
. і
і  , де
, де  ,
,  . Переконатися за допомогою геометричної побудови, що ці вектори можна додавати і віднімати за правилом паралелограма.
. Переконатися за допомогою геометричної побудови, що ці вектори можна додавати і віднімати за правилом паралелограма.
 .
. ,
,  ;
; ,
,  .
. в площині навколо точки
в площині навколо точки  до суміщення її з напрямком вектора
до суміщення її з напрямком вектора  , якщо обертання здійснюється проти годинкової стрілки, і j
, якщо обертання здійснюється проти годинкової стрілки, і j  при обертанні за годинковою стрілкою; якщо напрямок
при обертанні за годинковою стрілкою; якщо напрямок  .
.
 , де
, де 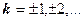 . Отже, за кут нахилу вектора
. Отже, за кут нахилу вектора  ціле число.
ціле число. називається будь-яке із значень кута нахилу вектора
називається будь-яке із значень кута нахилу вектора  , де
, де  .
. не визначається.
не визначається.
 (тобто значення з інтервалу
(тобто значення з інтервалу  ) називається головним значенням аргументу к.ч. і позначається
) називається головним значенням аргументу к.ч. і позначається  , тому
, тому  ,
, 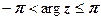 .
.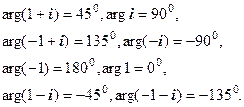

 . Пропонуємо довести цю тотожність самостійно.
. Пропонуємо довести цю тотожність самостійно.
 , то
, то 
 можна знаходити за формулою:
можна знаходити за формулою: (1.1)
(1.1) зображується точкою
зображується точкою  в другій чверті (рис.1.7). З
в другій чверті (рис.1.7). З 
 . Оскільки
. Оскільки  , то
, то 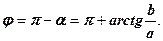
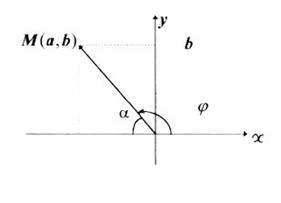
 за допомогою формул цього пункту.
за допомогою формул цього пункту. , (застосована формула (1.1),
, (застосована формула (1.1), 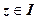 чверті);
чверті); , (формула (1.1),
, (формула (1.1),  чверті);
чверті); , (формула (1.1),
, (формула (1.1),  чверті);
чверті);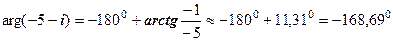 , (формула (1.1),
, (формула (1.1),  чверті);
чверті); ,
, .
.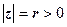 і аргумент
і аргумент  к.ч.
к.ч.  - полярні координати точки
- полярні координати точки  , яка зображає число
, яка зображає число  , вказаному на рис. 1.5, відомі формули переходу від полярних до прямокутних координат точки
, вказаному на рис. 1.5, відомі формули переходу від полярних до прямокутних координат точки  . Додамо ці рівності, помноживши другу на
. Додамо ці рівності, помноживши другу на  :
:
 2)
2)  3)
3) 
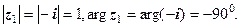


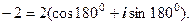

 .
. . Для переходу до тригонометричної форми необхідно:
. Для переходу до тригонометричної форми необхідно: і встановити, до якої чверті належить
і встановити, до якої чверті належить 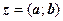 . На даному прикладі:
. На даному прикладі: 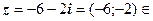 ІІІ четв. Див. рис.
ІІІ четв. Див. рис.
 (1)
(1)
 , ураховуючи при цьому властивість
, ураховуючи при цьому властивість .
. .
. . Для даного прикладу:
. Для даного прикладу:  ІІІ чверті. Маємо:
ІІІ чверті. Маємо:
 і
і  (2)
(2) маємо:
маємо:
 ,
, 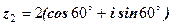 ;
; ;
; .
. ,
,  ;
; ;
; .
. то
то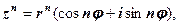 (1.3)
(1.3) . Обчислити
. Обчислити  .
.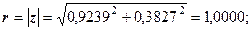
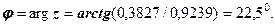
 застосовуємо формулу (1.3) при
застосовуємо формулу (1.3) при  :
:
 го степеня з числа
го степеня з числа 
 (1.4)
(1.4) символ
символ  означає корінь арифметичний з дійсного числа
означає корінь арифметичний з дійсного числа  .
. при
при  значень.
значень. .
. Застосовуємо формулу (1.4) при
Застосовуємо формулу (1.4) при 
 де
де 
 Відповідь:
Відповідь: 
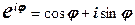 , (1.5)
, (1.5) будь-яке дійсне число.
будь-яке дійсне число. ) з чисто уявним показником, точніше, права частина в (1.5) просто позначена через
) з чисто уявним показником, точніше, права частина в (1.5) просто позначена через  , але це виправдано тим, що введений таким чином символ
, але це виправдано тим, що введений таким чином символ  буде володіти властивостями експоненти в дійсній області.
буде володіти властивостями експоненти в дійсній області.
 (
( .
. .
.
 . Покладемо
. Покладемо 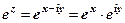 . Ця рівність є означенням експоненти з будь-яким показником.
. Ця рівність є означенням експоненти з будь-яким показником.
 (
( ціле);
ціле); 
 .
. то
то 


 .
.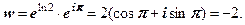
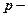 комплексне число,
комплексне число,  то
то 
 Очевидно, що
Очевидно, що 
 Якщо число
Якщо число  а потім застосувати формулу Ейлера (1.5), одержимо так звану показникову форму к.ч.
а потім застосувати формулу Ейлера (1.5), одержимо так звану показникову форму к.ч. .
. то
то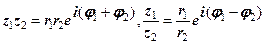 ;
; (
( .
.
 ІІІ чв.
ІІІ чв.

 ІІІ чв., то за формулою (1.1) §1.14 маємо:
ІІІ чв., то за формулою (1.1) §1.14 маємо:
 запишемо
запишемо 
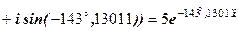 .
.


 обчислити наближено
обчислити наближено  (всі обчислення виконувати з чотирма знаками після коми). Для контролю знайти точне значення
(всі обчислення виконувати з чотирма знаками після коми). Для контролю знайти точне значення 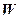 , виконуючи обчислення в алгебраїчній формі.
, виконуючи обчислення в алгебраїчній формі.





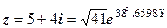 . 2.
. 2.  .
. . 4.
. 4.  .
.


