
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила приближенных вычисленийСтр 1 из 11Следующая ⇒
ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ Факультет «Прикладная математика и информационные технологии» Кафедра «Математика»
ВЫСШАЯ МАТЕМАТИКА
Учебно-методическое пособие для студентов первого курса бакалавриата, обучающихся по заочной форме по направлению 38.03.01 «Экономика»
Под редакцией профессора Н.Ш. Кремера
Рекомендовано кафедрой «Математика», протокол № 12 от 14 мая 2015 г.
Москва – 2015
ББК 22.3
Введение, методические указания и рекомендации по изучению дисциплины подготовил профессор Н.Ш. Кремер
Варианты контрольных работ подготовили: доц. Борисова Л.Р., доц. Путко Б.А., ст. преп. Федорова Н.И., доц. Шевелев А.Ю. Учебно-методическое пособие рекомендовано кафедрой «Математика». Зав. кафедрой «Математика» профессор В.Б.Гисин.
Высшая математика. Учебно-методическое пособие для студентов первого курса бакалавриата, обучающихся по заочной форме по направлению 38.03.01 «Экономика»./ Под ред. проф. Н.Ш. Кремера ‒ М.: Финуниверситет, 2015.
В учебно-методическом пособии приведен обзор основных понятий и положений дисциплины «Высшая математика», даны методические рекомендации по ее изучению, выделены типовые задачи с решениями, представлены контрольные вопросы для самопроверки и задачи для самоподготовки по данной дисциплине, приведены варианты контрольных работ (с примерами их решений) для студентов первого курса бакалавриата направления «Экономика», а также методические указания по их выполнению.
ББК 22.3 ПРЕДИСЛОВИЕ
Совершенствование деятельности в любой области экономики (управлении, финансово-кредитной сфере, маркетинге, учете, аудите) в значительной мере связано с применением в экономической науке и практике математических методов исследования. Цель курса математики в системе подготовки экономиста – освоение необходимого математического аппарата, помогающего анализировать, моделировать и решать прикладные экономические задачи. Изучаемые в математике методы и модели являются не только инструментами количественного расчета, средствами решения прикладных задач, но и эффективными методами проведения экономических исследований, элементами общей культуры.
Задачи изучения дисциплины «Высшая математика» вытекают из требований к результатам освоения программы бакалавриата, компетенций, установленных Образовательным стандартом высшего образования ФГОБУ «Финансовый университет при Правительстве РФ» (ОС ВО) по направлению 38.03.01 «Экономика». В процессе изучения дисциплины перед студентами ставятся следующие задачи: освоение приемов исследования и решения математически формализованных задач; использование классического математического аппарата для решения прикладных задач; выработка умения моделировать реальные объекты и процессы; развитие логического и алгоритмического мышления студентов; повышение уровня математической культуры студентов; развитие навыков самостоятельной работы по изучению учебной и научной литературы. В соответствии с ОС ВО по направлению «Экономика», квалификация академический бакалавр, процесс изучения дисциплины «Высшая математика» направлен на формирование следующих компетенций: общенаучных компетенций (ОНК) – способность использовать основные научные законы в профессиональной деятельности (ОНК-1); – владение культурой мышления, способность к восприятию, анализу и мировоззренческой оценке происходящих процессов и закономерностей (ОНК-2); инструментальных компетенций (ИК) – владение основными методами, способами и средствами получения, хранения и обработки информации (ИК-3) ‒ способность оформлять аналитические и отчеты н материалы по результатам выполненной работы (ИК-4); ‒ способность применять методики расчетов и основные методы исследований (ИК-5); социально-личностных компетенций (СЛК) – способность и готовность к продолжению образованию и к самообразованию (СЛК-1) – способность предлагать и обосновывать варианты управленческих решений (СЛК-3); системных компетенций (СК) – способность применять полученные знания на практике(СК-1); – способность анализировать, обобщать и систематизировать информацию (СК-2) – способность к постановке целей и задач исследований, выбору оптимальных путей и методов их достижения (СК-3);
профессиональных компетенций направления (ПКН) – владение основными научными понятиями и категориальным аппаратом современной экономики и их применение (ПКН-1); – способность применять математические методы для решения стандартных профессиональных финансово-экономических задач, интерпретировать полученные математические результаты (ПКН-3). В результате изучения дисциплины студент должен: а) знать основные понятия линейной алгебры и аналитической геометрии, дифференциального и интегрального исчислений, дифференциальных уравнений и рядов,, используемые в экономических исследованиях и при изучении других дисциплин естественнонаучного и профессионального циклов; б) уметь применятьосновные классические математические методы решения прикладных задач; строить математические модели прикладных задач; в) владеть навыками классического математического инструмента-рия для решения прикладных (экономических) задач. По дисциплине «Высшая математика» студенты бакалавриата направления «Экономика» должны выполнить две контрольные работы № 1 и № 2 (задания к которым приводятся в данном пособии). Контрольные работы (в соответствии с учебным графиком) могут быть существенно дополнены за счет частичного использования компьютерной обучающей программы (КОПР). В процессе изучения дисциплины студенты проходят компьютерное тестирование (если оно предусмотрено учебным планом) и сдают зачет по части 1 дисциплины «Линейная алгебра» и курсовой экзамен по части 2 дисциплины «Математический анализ» При выставлении итоговой оценки студента по данной дисциплине учитываются балльная оценка текущей успеваемости (качество подготовки и работа на практических занятиях, выполнение контрольных работ, компьютерное тестирование, посещение занятий) и результаты сдачи зачета и экзамена. . ВВЕДЕНИЕ
Цель настоящего методического пособия – помочь студентам в организации занятий при изучении общего курса математики. Для освоения данной дисциплины в вузе записаны видео-лекции, проводятся практические занятия. Основной формой обучения в условиях заочного вуза является самостоятельная работа с видео-лекциями, учебником и учебными пособиями (с. 65). Дополнительно для самостоятельного изучения дисциплины рекомендуются Интернет-ресурсы: компьютерная обучающая программа (КОПР), обзорная лекция, электронная учебно-методическая литература и др., размещенные на сайте университета. В помощь студентам в университете и его филиалах функционируют учебно-методические кабинеты, которые позволяют осуществить выход в Интернет, поработать с Интернет-ресурсами института, компьютерными обучающими программами и электронными версиями учебно-методической литературы по данной дисциплине, пройти тестирование в режиме самоконтроля. Каждый студент с самого начала занятий должен выработать для себя рациональную систему работы над курсом и постоянно практиковаться в решении задач. В противном случае усвоение и практическое использование учебного материала затруднены. Чрезвычайно важны систематические занятия. Работа урывками не приносит положительных результатов. Студент должен вести конспект (рабочую тетрадь). Рекомендуется конспектировать определения, формулировки теорем, схемы их доказательств, формулы и решения задач. Формулы следует выписывать в специальные таблицы для каждой части (раздела) курса. Постоянное пользование конспектом, в частности таблицами формул, способствует их запоминанию и дает возможность решать примеры и задачи, не обращаясь к учебным пособиям.
Часто приходится слышать высказывания студентов о том, что теорию они знают, а решать задачи не умеют. Это свидетельствует о неглубоком усвоении учебного материала. Нужно решать как можно больше задач. Начинать следует с наиболее простых, элементарных, а затем переходить к более сложным. По такому принципу и расположены задачи в рекомендуемых учебных пособиях. Решение следует доводить до окончательного результата, промежуточные преобразования выполнять последовательно и аккуратно. Если задача связана с отысканием численного результата, то подстановку численных значений вместо букв лучше производить только в окончательно упрощенное выражение. Если материал учебника, учебного или методического пособия, КОПР не дает ответа на возникший вопрос, то следует обратиться за консультацией (по электронной почте)) на кафедру «Математика». Для получения письменной консультации необходимо указать, каким учебником (пособием, КОПР) вы пользовались (автор, наименование, год издания) и какое конкретное место в учебнике не понятно. Если появились затруднения в решении задачи, укажите, каким способом вы пытались ее решить. Лишь в этом случае преподаватель сможет оказать вам помощь. При решении различных задач нередко приходится вычислять приближенно значения функции, определенного интеграла и др. Незнание правил приближенных вычислений часто приводит к тому, что их результаты оказываются не только неточными, но и ошибочными, настолько они далеки от истинных (точных) значений. При этом многие стремятся удержать больше цифр в окончательном ответе, показать, какой «высокой» степени точности они добились. Точность такого ответа, как правило, оказывается ложной, так как определенное число последних цифр просто ошибочно. Чтобы этого не случилось, необходимо знать и применять правила приближенных вычислений (см. с.7‒9). Ими надлежит пользоваться при выполнении арифметических операций с приближенными числами и для получения приближенного результата. Часть 1.
ЛИНЕЙНАЯ АЛГЕБРА Тема 4. Линейные операторы Понятие линейного оператора. Образ и прообраз векторов. Матрица линейного оператора в заданном базисе. Ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы. Собственные векторы и собственные значения линейного оператора (матрицы). Характеристический многочлен матрицы. Диагональный вид матрицы линейного оператора в базисе, состоящем из его собственных векторов. ([1 или 6, § 3.6, 3.7]; [2 или 7, § 3.3, 3.4], или [3, § 3.6, 3.7, 3.12,3.13], или [4, § 3.8, 3.10, 3.18, 3.19]). . В этой теме рассматривается одно из базовых понятий линейной алгебры – понятие линейного оператора (преобразования, отображения), представляющего закон (правило), по которому каждому вектору х n -мерного пространства Линейность оператора определяется выполнением свойств аддитивности и однородности оператора [1, или 6, или 3, § 3.6]. Нужно знать, что каждому линейному оператору Особую роль в приложениях линейной алгебры играют векторы, которые под воздействием линейного оператора Если базис линейного оператора составить из собственных векторов, то матрица оператора имеет наиболее простой вид и представляет собой диагональную матрицу, а соответствующая операция называется приведением данной матрицы к диагональному виду ([1, или 6, или 3, пример 3.8]).
Тема 5. Квадратичные формы Квадратичная форма (определение). Матрица квадратичной формы. Матричная форма записи квадратичной формы.. Канонический вид и ранг квадратичной формы. Закон инерции квадратичных форм. Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерий определенности квадратичной формы через собственные значения ее матрицы. Критерий Сильвестра. ([1 или 6, § 3.8]; [2 или 7, § 3.5], или [3, § 3.8, 3.14], или [4, § 3.11, 3.13, 3.20]). Квадратичные формы достаточно часто возникают при решении прикладных задач. Если в n -мерном линейном пространстве выбрать некоторый базис, то квадратичную форму Необходимо знать определение и матричную запись квадратичной формы, ее канонический вид. Уметь приводить в простых случаях квадратичную форму к каноническому виду, имея в виду, что это возможно сделать многими способами, но ранг квадратичной формы при этом не меняется. Студент должен владеть двумя способами исследования на знакоопределенность квадратичной формы (с помощью собственных значений ее матрицы и критерия Сильвестра). Например, очевидно, что квадратичная форма
Часть 2. МАТЕМАТИЧЕСКИЙ АНАЛИЗ Тема 7. Функции
Понятие о множествах. Действительные числа и числовые множества. Постоянные и переменные величины. Функции и способы их задания. Область определения функции. Четные, нечетные, монотонные и ограниченные функции. Сложная функция. Понятие элементарной функции. Основные элементарные функции и их графики. Неявные функции. ([1 или 6, § 5.1 – 5.5, 5.7]; [2 или 7, гл. 5], или [3, §5.1 – 5.5, 5.7], или [5, §1.1 – 1.5, 1.7]). Прежде всего полезно ознакомиться с некоторыми логическими символами и кванторами, чтобы использовать их в дальнейшем для сокращения записей ([1, или 6, или 3, § 5.1, 6.1]). Изучение темы следует начать с основных понятий теории множеств ([1 или 6, или 3, § 5.1]). Далее нужно четко усвоить важнейшее понятие математического анализа – функции, уметь находить область ее определения, знать способы задания функции: аналитический, графический, табличный, словесный. В нашем курсе рассматриваются в основном элементарные функции. Студент должен уяснить определение элементарной функции ([1, или 6, или 3, § 5.5]), четко знать свойства и строить графики следующих основных элементарных функций: y = C (постоянная), y = xn (степенная), y = ax (показательная), y = log ax (логарифмическая). Необходимо усвоить понятие сложной функции (функции от функции). Построение графика четной (нечетной) функции можно значительно упростить, если учесть, что графики четных функций симметричны относительно оси Оy, а нечетных – относительно начала координат. Одним из характерных свойств функции является монотонность (т.е. ее возрастание или убывание на каком-либо промежутке). Тема завершается рассмотрением линейной функции и элементов аналитической геометрии на плоскости – простейших уравнений прямой. Этот материал будет использоваться на III курсе при изучении дисциплин «Методы оптимальных решений», «Исследование операций». Основополагающее значение здесь имеет определение уравнения линии на плоскости как уравнения с двумя переменными x и y, которому удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на ней. Из этого определения следуют два важных для практики положения. 1. Если задано уравнение линии, то можно установить, принадлежит ли ей какая-либо точка плоскости. Для этого достаточно подставить координаты точки в уравнение линии вместо переменных x и y. Если окажется, что они удовлетворяют уравнению, то точка принадлежит линии, в противном случае – не принадлежит. 2. Координаты точки пересечения двух линий, заданных своими уравнениями, удовлетворяют обоим уравнениям. Поэтому для нахождения координат точки пересечения двух линий нужно решить систему, составленную из их уравнений. Студент должен знать простейшие виды уравнений прямой и уметь пользоваться ими при решении задач. Соответствующий учебный материал приведен в учебнике ([1, или 6,или 3, § 4.2]). Обратите особое внимание на нахождение уравнений прямых, параллельной и перпендикулярной данной прямой ([1, или 6, или 3, пример 4.5].
Тема 9. Производная
Задачи (о касательной к плоской кривой и о мгновенной скорости), приводящие к понятию производной. Производная, ее геометрический, механический и экономический смысл. Уравнение касательной к плоской кривой. Дифференцируемость функции. Связь между дифференцируемостью и непрерывностью функции (необходимый признак дифференцируемости). Основные правила и основные формулы дифференцирования. Формулы производных основных элементарных функций. Производная сложной функции. Техника дифференцирования. Производные высших порядков ([1 или 6, § 7.1 – 7.7]; [2 или 7, § 7.1 – 7.3], или [3, § 7.1 – 7.7, 7.11, 7.12], или [5, §3.1 – 3.7, 3.11, 3.12]).). Студенты должны знать две классические задачи, которые приводят к понятию производной: задачу о касательной к плоской кривой и задачу о скорости неравномерного прямолинейного движения. Их решение выявляет геометрический и механический смысл производной. Нужно четко знать определение производной, представлять ее экономический смысл ([1или 6, § 7.6] или [3, § 7.10]), уметь составить уравнение касательной к графику любой функции y = f (x) в заданной точке. Изучая материал этой темы, студенты знакомятся с необходимым условием дифференцируемости функции. Необходимо четко уяснить, что из дифференцируемости функции в некоторой точке следует ее непрерывность в этой точке. Обратная теорема не справедлива, так как существуют непрерывные функции, которые в некоторых точках могут не иметь производной ([1 или 6, § 7.2] или [3, § 7.2]). Нужно, чтобы студенты, хорошо усвоив основные правила дифференцирования, умели находить производную суммы и произведения нескольких дифференцируемых функций, производную частного двух функций, пользоваться основными формулами дифференцирования, а также могли их вывести. Таблица основных формул приведена в учебнике ([1 или 6, или 3, § 7.5]) и на переднем форзаце. Наиболее важным для овладения техникой дифференцирования функций, и к тому же наиболее трудным, является правило дифференцирования сложной функции ([1, или 6, или 3, §7.4]). Знание этого правила способствует успешному освоению техники дифференцирования функций. Поэтому необходимо обратить особое внимание на примеры с решениями, в которых иллюстрируется его применение. Нужно усвоить понятия производных высших порядков и уметь их находить.
Раздел VI. РЯДЫ
Тема 16. Числовые ряды Понятие числового ряда. Сходимость ряда и его сумма. Свойства сходящихся рядов. Необходимый признак сходимости (доказать). Расходимость гармонического ряда. Достаточные признаки сходимости знакоположительных рядов: признак сравнения, Даламбера. Знакопеременные ряды. Признак Лейбница сходимости знакочередующихся рядов. Абсолютная и условная сходимость. ([1 или 6, § 13.1–13.5]; [2 или 7, § 13.1 – 13.3], или [3, §13.1 – 13.7], или [5, §9.1 – 9.7]. При изучении данной темы студенты знакомятся с новой формой изучения числовой последовательности. Следует уяснить, что обозначение Нужно уяснить, что необходимый признак сходимости (для сходящихся рядов Применяя признаки сравнения, можно использовать в качестве «эталонных» следующие ряды: 1) геометрический ряд 2) гармонический ряд 3) обобщенный гармонический ряд К признаку сравнения обращаются тогда, когда признак Даламбера показывает, что Говоря о сходимости знакочередующихся рядов, следует иметь в виду два типа сходимости: абсолютную и условную. Важность этих понятий связана с тем, что абсолютно сходящиеся ряды обладают некоторыми свойствами конечных сумм в отличие от условно сходящихся рядов. Решать вопрос о сходимости знакочередующегося ряда рекомендуем в таком порядке. 1. Составить ряд из абсолютных величин членов данного знакочередующегося ряда. 2. Исследовать сходимость полученного ряда. Может оказаться, что этот ряд сходится. Тогда исходный ряд также сходится, и притом абсолютно. Задача решена. Если же составленный ряд расходится, то в этом случае о сходимости или расходимости исходного ряда сделать вывод нельзя; необходимо выполнить пункт 3. 3. Исследовать условную сходимость исходного знакочередующегося ряда, например, по признаку Лейбница.
Вопросы для самопроверки Часть I. Линейная алгебра 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц. 2. Определители 2, 3 и n -го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца. 3. Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления. 4. Понятие минора k- го порядка. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований. Пример. 5. Линейная независимость строк (столбцов) матрицы. Теорема о ранге матрицы. 6. Система п линейных уравнений с п переменными (общий вид). Матричная форма записи такой системы. Решение системы (определение). Совместные и несовместные, определенные и неопределенные системы линейных уравнений. 7. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса. 8. Система m линейных уравнений с n переменными. Теорема Кронекера – Капелли. Условие определенности и неопределенности любой системы линейных уравнений. 9. Базисные (основные) и свободные (неосновные) переменные системы m линейных уравнений с n переменными. Базисное решение. 10. Система линейных однородных уравнений и ее решения. Условие существования ненулевых решений такой системы. 11. Векторы на плоскости и в пространстве (геометрические векторы). Линейные операции над векторами (сложение, умножение вектора на число). Коллинеарные и компланарные векторы. 12. Скалярное произведение двух векторов (определение) и его выражение в координатной форме. Угол между векторами. 13. n -мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов. 14. Векторное (линейное) пространство. Его размерность и базис. Теорема о существовании и единственности разложения вектора линейного пространства по векторам базиса. 15. Скалярное произведение векторов в n -мерном пространстве. Евклидово пространство. Длина (норма) вектора. 16. Ортогональные векторы. Ортогональный и ортонормированный базисы. Теорема о существовании ортонормированного базиса в евклидовом пространстве. 17. Определение оператора. Понятие линейного оператора. Образ и прообраз векторов. 18. Матрица линейного оператора в заданном базисе: связь между вектором х и образом у. Ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы. 19. Собственные векторы и собственные значения оператора 20. Матрица линейного оператора в базисе, состоящем из его собственных значений. Пример. 21. Квадратичная форма (определение). Матрица квадратичной формы. Ранг квадратичной формы. Пример. 22. Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Пример. Закон инерции квадратичных форм. 23. Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерии знакоопределенности квадратичной формы (через собственные значения ее матрицы и по критерию Сильвестра). 24. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести). 25. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых. 26. Кривые второго порядка, их общее уравнение. Нормальное уравнение окружности. Каноническое уравнение эллипса. Геометрический смысл параметров окружности и эллипса. 27. Канонические уравнения гиперболы и параболы. Геометрический смысл их параметров. Уравнение асимптот гиперболы. График обратно-пропорциональной зависимости и квадратного трехчлена. 28. Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости. Условия параллельности и перпендикулярности двух плоскостей. 29. Уравнения прямой линии в пространстве как линии пересечения двух плоскостей. Канонические уравнения прямой. Направляющий вектор прямой. Условия параллельности и перпендикулярности двух прямых в пространстве. 30. Углы между двумя плоскостями, двумя прямыми, между прямой и плоскостью. Условия их параллельности и перпендикулярности.
ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ ВАРИАНТ 1 (для студентов, номера личных дел которых оканчиваются цифрой 1) Контрольная работа № 1 1. Даны матрицы
Найти ранг матрицы 2. По формулам Крамера решить систему:
3. Решить систему линейных уравнений:
Найти какое-нибудь базисное решение. 4. Даны четыре вектора
в некотором базисе. Показать, что векторы 5. Найти собственные значения и собственные векторы линейного оператора 6. Даны уравнения двух сторон прямоугольника 7. Найти расстояние от плоскости Контрольная работа № 2 1. Найти предел:
2. Составить уравнения касательных к графику функции 3. Исследовать функцию
5. Вычислить площадь фигуры, ограниченной линиями 6. Экспериментальные данные о переменных х и у приведены в таблице:
В результате их выравнивания получена функция 7. Решить дифференциальное уравнение:
8. Исследовать сходимость ряда:
ВАРИАНТ 2 (для студентов, номера личных дел которых оканчиваются цифрой 2) Контрольная работа № 1 1. Даны матрицы
Найти ранг матрицы 2. Методом обратной матрицы решить систему:
3. Определить, имеет ли однородная система
ненулевое решение. Найти общее решение системы. 4. Даны четыре вектора
в некотором базисе. Показать, что векторы 5. а) Методом Лагранжа привести квадратичную форму f (x 1, x 2)=3 x 12+ x 22- x 1 x 2) f (x 1, x 2)= x 12+5 x 22+4 x 1 x 2 к каноническому виду (указать пример соответствующего преобразования координат). б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму f (x 1, x 2, x 3)= x 12 + 3 x 22 + 4 x 32 +2 x 1 x 2+2 x 1 x 3 +6 x 2 x 3.. 6. Составить уравнение прямой, проходящей через вершину прямого угла треугольника 7. Найти угол между плоскостью Контрольная работа № 2
|
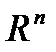 ставится в соответствие один вектор y m -мерного пространства
ставится в соответствие один вектор y m -мерного пространства 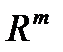 . При
. При 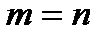 оператор обращает
оператор обращает  соответствует матрица А в некотором базисе
соответствует матрица А в некотором базисе 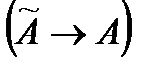 . Верно и обратное утверждение
. Верно и обратное утверждение 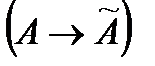 . С помощью этой матрицы для любого вектора х можно найти его образ – вектор y.
. С помощью этой матрицы для любого вектора х можно найти его образ – вектор y.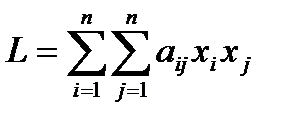 можно рассматривать как некоторую функцию векторного аргумента
можно рассматривать как некоторую функцию векторного аргумента 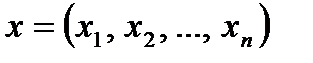 .
.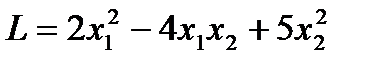 (т.е.
(т.е. 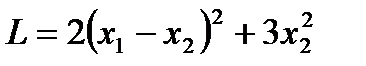 ) является знакоположительной. В этом можно убедиться с помощью отмеченных критериев, ибо матрица квадратичной формы
) является знакоположительной. В этом можно убедиться с помощью отмеченных критериев, ибо матрица квадратичной формы 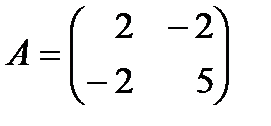 , как нетрудно показать, имеет положительные собственные значения
, как нетрудно показать, имеет положительные собственные значения 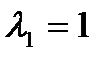 ,
, 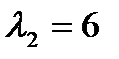 , а угловые (главные) миноры
, а угловые (главные) миноры 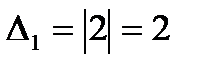 ,
, 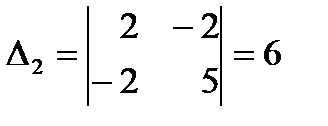 также положительные. А квадратичная форма
также положительные. А квадратичная форма 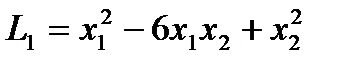 не является знакоопределенной, так как ее матрица
не является знакоопределенной, так как ее матрица 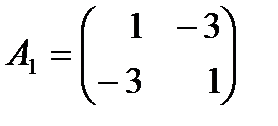 имеет разные по знаку собственные значения
имеет разные по знаку собственные значения 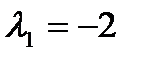 и
и 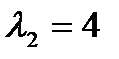 , а угловые миноры
, а угловые миноры 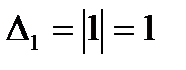 ,
, 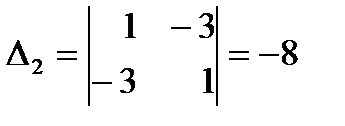 чередуются по знаку, начиная с положительного значения (при
чередуются по знаку, начиная с положительного значения (при 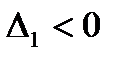 ,
, 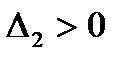 квадратичная форма была бы знакоотрицательной) – (см. [1 или 6, примеры 3.11, 3.12], или [3, примеры 3.11, 3.12, 3.109, 3.110]).
квадратичная форма была бы знакоотрицательной) – (см. [1 или 6, примеры 3.11, 3.12], или [3, примеры 3.11, 3.12, 3.109, 3.110]).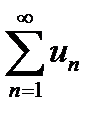 , или u 1 + u 2 + …+ un + …, – символ, который не следует смешивать с обычной (конечной) суммой. Сумма и сходимость ряда определяется через предельный переход. При рассмотрении ряда могут решаться задачи: определение его суммы и исследование сходимости. Решение первой задачи «перекрывает» и вторую, но это не всегда возможно или вызывает значительные трудности. Решение второй задачи не менее важно, так как в случае, если ряд сходится, его сумма существует и ее можно найти приближенно с любой степенью точности, взяв сумму достаточного числа его первых членов.
, или u 1 + u 2 + …+ un + …, – символ, который не следует смешивать с обычной (конечной) суммой. Сумма и сходимость ряда определяется через предельный переход. При рассмотрении ряда могут решаться задачи: определение его суммы и исследование сходимости. Решение первой задачи «перекрывает» и вторую, но это не всегда возможно или вызывает значительные трудности. Решение второй задачи не менее важно, так как в случае, если ряд сходится, его сумма существует и ее можно найти приближенно с любой степенью точности, взяв сумму достаточного числа его первых членов.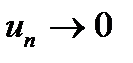 при
при 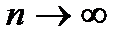 ) не является достаточным, но из необходимого признака сходимости следует, что если предел общего члена
) не является достаточным, но из необходимого признака сходимости следует, что если предел общего члена  , то ряд расходится. Поэтому исследование сходимости числового ряда рекомендуется начинать с вычисления предела его общего члена (если он находится не очень сложно). Если предел окажется равным нулю, то это означает, что ряд может сходиться. Чтобы установить, сходится ли ряд, далее применяют достаточные признаки сходимости.
, то ряд расходится. Поэтому исследование сходимости числового ряда рекомендуется начинать с вычисления предела его общего члена (если он находится не очень сложно). Если предел окажется равным нулю, то это означает, что ряд может сходиться. Чтобы установить, сходится ли ряд, далее применяют достаточные признаки сходимости. – сходится при | q |<1, расходится при
– сходится при | q |<1, расходится при 
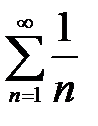 – расходится;
– расходится; – сходится при
– сходится при 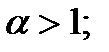 расходится при
расходится при 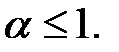
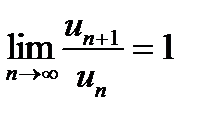 . Во всех этих случаях применения достаточных признаков сходимости речь идет об исследовании рядов с положительными членами.
. Во всех этих случаях применения достаточных признаков сходимости речь идет об исследовании рядов с положительными членами.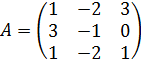 и
и 
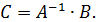
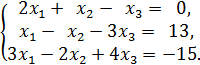
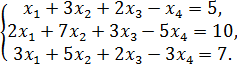
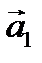 =(2;4; – 6);
=(2;4; – 6); 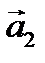 =(1;3;5);
=(1;3;5); 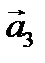 =(0; – 3;7);
=(0; – 3;7); 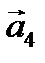 =(3;2;52)
=(3;2;52)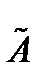 , заданного матрицей А =
, заданного матрицей А = 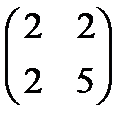 .
.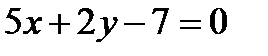
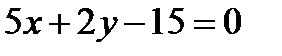 и уравнение его диагонали
и уравнение его диагонали 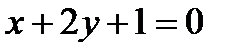 . Составить уравнения остальных сторон и второй диагонали этого прямоугольника. Сделать чертеж.
. Составить уравнения остальных сторон и второй диагонали этого прямоугольника. Сделать чертеж.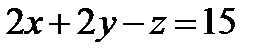 до начала координат.
до начала координат.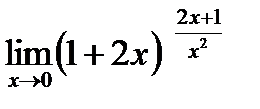 .
.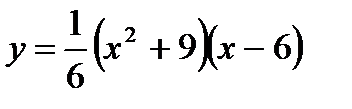 в точках ее пересечения с осями координат. Сделать чертеж.
в точках ее пересечения с осями координат. Сделать чертеж.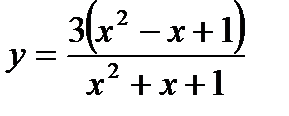 и построить схематично ее график.
и построить схематично ее график.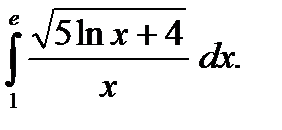
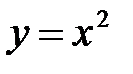 ,
, 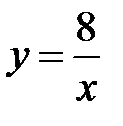 ,
, 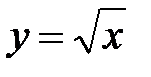 . Сделать чертеж.
. Сделать чертеж.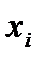
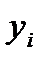
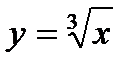 . Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 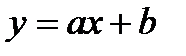 (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.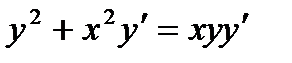 .
.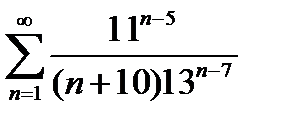
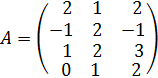 и
и 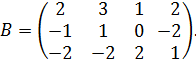
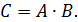
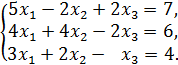
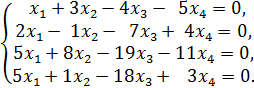
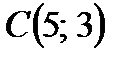 и центр описанной окружности, если координаты остальных вершин треугольника
и центр описанной окружности, если координаты остальных вершин треугольника 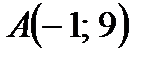 и
и 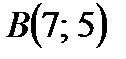 . Сделать чертеж.
. Сделать чертеж.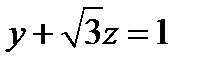 и линией пересечения плоскостей
и линией пересечения плоскостей 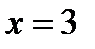 и
и 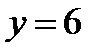 .
. .
.
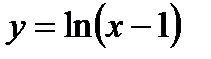 , перпендикулярно прямой, образующей с положительным направлением оси Ох угол 135°. Сделать чертеж.
3. Исследовать функцию
, перпендикулярно прямой, образующей с положительным направлением оси Ох угол 135°. Сделать чертеж.
3. Исследовать функцию 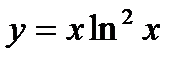 и построить схематично ее график.
и построить схематично ее график.
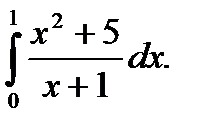
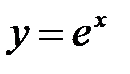 ,
, 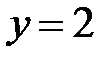 ,
, 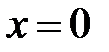 . Сделать чертеж.
. Сделать чертеж.


