
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показникова форма комплексного числа
Наведемо (без доведення) деякі відомості із математичного аналізу, які потрібні для введення показникової форми комплексного числа. Означення. Числовою послідовністю називають функцію Позначають послідовність так: При цьому Дамо означення границі числової послідовності дійсних чисел. Означення. Число
Позначають границю так: Розглянемо числову послідовність
Запишемо декілька членів цієї послідовності:
Послідовність
Можна довести, що границя послідовності
Розглянемо послідовність комплексних чисел
Означення. Число
Позначають границю так:
Нехай існують границі послідовностей дійсної і уявної частини комплексних чисел:
Границя послідовності комплексних чисел
Означення. Функцією комплексної змінної
Рис. 12 Позначається комплексна функція так Одну із комплексних функцій ми розглянули, коли виконували операцію добування кореня із комплексного числа:
Функцію комплексної змінної
З іншої сторони, функцію дійсної змінної
Наведемо також розвинення в ряди функцій
Аналогічні формули розвинення в ряди мають місце і для функцій комплексної змінної. А саме,
Нехай
Таким чином,
Заміняючи
Якщо додати ліві і праві частини рівностей (31) та (32), то дістанемо, що
Якщо відняти ліві і праві частини рівностей (31) та (32), то дістанемо, що Після заміни
Якщо у формулі (31) замінити
Запишемо комплексне число
Представлення комплексного числа
називається показниковою формою комплексного числа. При цьому
Властивості функції Розглянемо показникову функцію Маємо Або
Звідки отримуємо, що модуль 11.1. Для показникової функції мають місце формули
Доведемо першу із формул (37). Нехай
Інші формули (37) доводяться аналогічно. Доведіть їх самостійно.
11.2. Функція Покажемо це. Використовуємо формулу (37) і показникову форму функції
11.3. Періодом функції
Дійсно, 11.4. Крім Нехай Нехай Приклад. Записати число Розв’язання. Використаємо формули (37) і формули Ейлера (33):
Враховуючи, що згідно з формулами (13)
11.5. Запишемо в показниковій формі дійсні числа
Таким чином, крім формул (13) запису в тригонометричній формі дійсних чисел
Наведемо ще одну комплексну функцію
Приклад 1. Знайти Згідно з означення логарифму комплексного числа маємо Приклад 2. Знайти Для заданої функції
ЛЕКЦІЯ 3.
|
||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.108 (0.029 с.) |
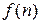 , аргументом якої є натуральне число
, аргументом якої є натуральне число  .
. , або
, або  , або
, або 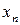 .
. називається границею числової послідовності
називається границею числової послідовності  існує такий номер
існує такий номер 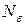 , який залежить від
, який залежить від 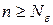 виконується нерівність
виконується нерівність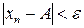 .
.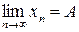 .
. . (27)
. (27)
 , тобто
, тобто .
.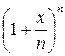 є функція
є функція 
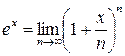 . (28)
. (28) де
де 
 називається границею послідовності комплексних чисел
називається границею послідовності комплексних чисел 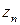 , якщо для будь-якого, наперед заданого, достатньо малого, додатного числа
, якщо для будь-якого, наперед заданого, достатньо малого, додатного числа 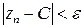 .
.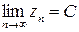 .
. Враховуючи, що
Враховуючи, що 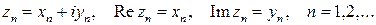 , маємо
, маємо .
.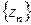 існує тоді і тільки тоді, коли існують границі послідовностей дійсних чисел
існує тоді і тільки тоді, коли існують границі послідовностей дійсних чисел  .
.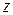 називається правило, за яким кожному комплексному значенню
називається правило, за яким кожному комплексному значенню  комплексної площини ставиться у відповідність одне або декілька значень із області
комплексної площини ставиться у відповідність одне або декілька значень із області 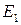 іншої комплексної площини.
іншої комплексної площини.
 .
. . При цьому одному значенню комплексної змінної
. При цьому одному значенню комплексної змінної  ,
, 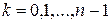 .
. визначимо аналогічно тому, як визначали функцію дійсної змінної
визначимо аналогічно тому, як визначали функцію дійсної змінної  , тобто
, тобто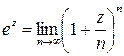 .
.
 . (29)
. (29) та
та 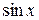
 ,
,  .
.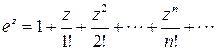
 . Тоді, враховуючи ряди для функцій
. Тоді, враховуючи ряди для функцій 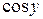 та
та 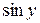 , маємо
, маємо
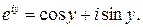 (31)
(31)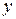 на
на  , дістаємо
, дістаємо 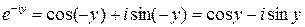 або
або
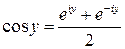 .
. .
. в цих формулах маємо формули Ейлера
в цих формулах маємо формули Ейлера ,
,  . (33)
. (33)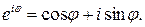 (34)
(34)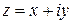 у тригонометричній формі:
у тригонометричній формі: . Із формули (34) дістаємо, що
. Із формули (34) дістаємо, що  , тоді число
, тоді число 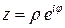 .
.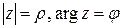 .
. .
. . (36)
. (36) функції
функції  ,
,  , а аргумент функції
, а аргумент функції  .
.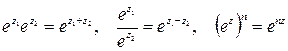 . (37)
. (37) . Використаємо представлення функції
. Використаємо представлення функції 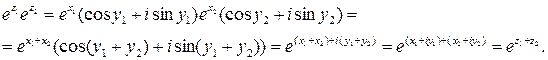
 .
. . Маємо
. Маємо 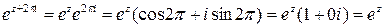 , тобто
, тобто . (38)
. (38) , де
, де 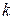 — ціле число:
— ціле число: ,
, .
.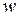 — період функції, тобто
— період функції, тобто 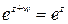 . Звідки при
. Звідки при  маємо
маємо  .
. . Тоді
. Тоді  або
або 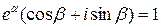 , тобто
, тобто  . Звідки
. Звідки 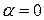 і
і  . Тоді
. Тоді  . Отже,
. Отже,  , а це і означає, що інших переодів, крім
, а це і означає, що інших переодів, крім  в алгебраїчній, тригонометричній і показниковій формі.
в алгебраїчній, тригонометричній і показниковій формі. . Задане число має вигляд в алгебраїчній формі:
. Задане число має вигляд в алгебраїчній формі: 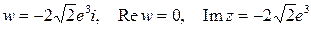 .
.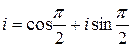 , маємо задане число в тригонометричній формі
, маємо задане число в тригонометричній формі 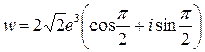 . Задане комплексне число
. Задане комплексне число 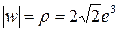 і аргумент
і аргумент  . Отже, в показниковій формі
. Отже, в показниковій формі 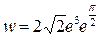 .
.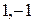 та уявні числа
та уявні числа 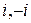 , використовуючи їх тригонометричну форму(13). Маємо
, використовуючи їх тригонометричну форму(13). Маємо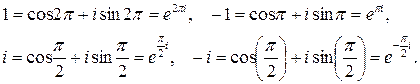
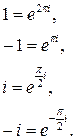 (39)
(39) . Натуральним логарифмом комплексного числа
. Натуральним логарифмом комплексного числа  .
. .
. .
. .
. . Знаходимо модуль
. Знаходимо модуль  і аргумент
і аргумент  заданого числа. Таким чином,
заданого числа. Таким чином,  .
.


