
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совместная, несовместная СЛАУ.Содержание книги Поиск на нашем сайте Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений. Определённая, неопределённая СЛАУ. Если СЛАУ имеет решение и при том единственное, то её называют определённой а если решение неединственное – то неопределённой. МАТРИЧНЫЕ УРАВНЕНИЯ Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Найдем произведение т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением. Пусть определитель матрицы отличен от нуля | A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Формулы Крамера Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А: D = det (ai j) и n вспомогательных определителей D i (i= Формулы Крамера имеют вид: D × x i = D i (i = Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: x i = D i / D. Если главный определитель системы D и все вспомогательные определители D i = 0 (i= Теорема (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём Доказательство: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения: Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и Наконец несложно заметить, что Таким образом, получаем равенство: Аналогично выводятся равенства Теорема Кронекера - Капелли. Система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы Доказательство: Оно распадается на два этапа. 1. Пусть система имеет решение. Покажем, что Пусть набор чисел 2. Пусть
Положим
В силу равенства (1) В рассмотренной выше системе Замечание:Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса) Пусть дана система Выпишем расширенную матрицу системы
Назовем элементарными операциями следующие действия с матрицами: 1. перестановка строк; 2. умножение строки на число, отличное от нуля; 3. сложение строки с другой строкой, умноженной на число. Отметим, что при решении системы уравнений, в отличие от вычисления определителя и нахождения ранга, нельзя оперировать со столбцами. Если по матрице, полученной из Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице
(Первые нулевые столбцы, как правило, отсутствуют.) Если в матрице Этому уравнению не удовлетворяет ни один набор чисел Матрицу где
По отношению к матрице
где
и к матрице Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее. Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида
Далее выполняется так называемый обратный ход метода Гаусса. По матрице Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы Ax=b. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами Если система была однородной, то получим общее решение однородной системы. Коэффициенты при Способ 2: Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одной переменной, перенесенной в правую часть, нужно присвоить значение 1, а остальным - нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другой переменной в правой части значение 1, а остальным - нули, получим второе решение из фундаментальной системы и т.д. Определение: система называется совместно й, если она имеет хотя бы одно решение, и несовместной -- в противном случае, то есть в случае, когда решений у системы нет. Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных. Например, система из трех уравнений с двумя неизвестными
имеет решение
решений не имеет, то есть является несовместной. Определение: Расширенной матрицей системы линейных уравнений называется матрица
Следствие: Ранг расширенной матрицы Доказательство: Так как любая линейно независимая система столбцов матрицы A является линейно независимой системой столбцов матрицы Пусть Квадратные системы с невырожденной матрицей. Система называется квадратной, если число m ее уравнений равно числу n неизвестных, то есть когда ее матрица A -- квадратная матрица. Решение СЛАУ: Пусть дана СЛАУ
……. … …… Am1x1 + … + amnxn = 0 Данная система всегда совместна так как имеет тривиальное решение х1=…=хn=0 Для существования нетривиальных решений необходимо и достаточно выполнение словия r = r(A) < n, что равносильно условию det(A)=0, когда матрица А – квадратная. Th Совокупность решений СЛАУ образует линейное пространство размерности (n-r). Это означает, что произведение ее решения на число, а также сумма и линейная комбинация конечного числа ее решений является решениями этой системы. Линейное пространство решений любой СЛАУ является подпространством пространства Rn. Любая совокупность (n-r) линейно независимых решений СЛАУ (являющаяся базисом в пространстве решений) называется фундаментальной совокупностью решений(ФСР). Пусть х1,…,хr - базисные неизвестные, хr+1,…,хn – свободные неизвестные. Свободным переменным дадим поочередно следующие значения:
хr+2=0 хr+2=1 хr+2=0 …… …… …… хn=0 хn=0 хn=1 Определив значения базисных переменных, соответствующие каждому набору значений свободных переменных, получим решения: Х1 (1) Х1 (2) Х1 (n-r) …… …… ……. Х(1) = 1 0 0 0 1 0 0 0 1 Построенная таким образом система решений системы уравнений называется нормальной фундаментальной совокупностью решений. Теорема. Множество всех решений однородной системы уравнений
……. … …… Am1x1 + … + amnxn = 0 Образует линейное пространство S (пространство решений), которое является подпространством в Rn (n – число неизвестных), причем dims=k=n-r, где r- ранг системы. Базис в пространстве решений{x (1),…, x (k)} называется фундаментальной системой решений, и общее решение имеет вид: X=c1x (1) + … + ckx (k), c (1),…, c (k)? R
|
||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 3831; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

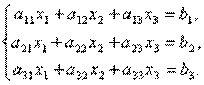 Рассмотрим матрицу системы
Рассмотрим матрицу системы 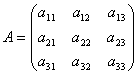 и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов 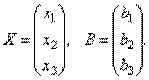
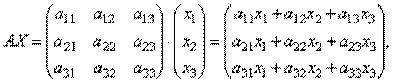
 или короче A ∙ X=B.
или короче A ∙ X=B.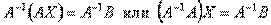 . Поскольку A-1A = E и E ∙ X = X, то получаем решение матричного уравнения в виде X = A-1B.
. Поскольку A-1A = E и E ∙ X = X, то получаем решение матричного уравнения в виде X = A-1B.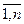 ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.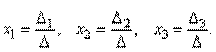

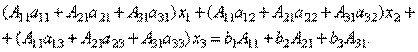
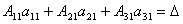 .
.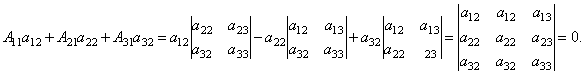
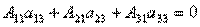 .
.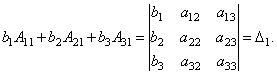
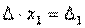 . Следовательно,
. Следовательно, 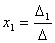 .
.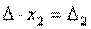 и
и  , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.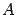 равен рангу расширенной матрицы
равен рангу расширенной матрицы 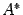 .
.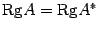 .
.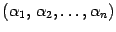 является решением системы. Обозначим через
является решением системы. Обозначим через 
 -ый столбец матрицы
-ый столбец матрицы  . Тогда
. Тогда  , то есть столбец свободных членов является линейной комбинацией столбцов матрицы
, то есть столбец свободных членов является линейной комбинацией столбцов матрицы 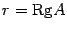 . Предположим, что
. Предположим, что 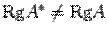 . Тогда по
. Тогда по  . Выберем в
. Выберем в 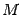 . Он имеет порядок
. Он имеет порядок 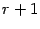 . Столбец
. Столбец 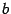 свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы
свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы  , где
, где  -- определитель, который получается из минора
-- определитель, который получается из минора  . Если столбец
. Если столбец  проходил через минор M, то в
проходил через минор M, то в  , будет два одинаковых столбца и, следовательно,
, будет два одинаковых столбца и, следовательно, 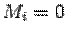 . Если столбец
. Если столбец  не проходил через минор
не проходил через минор  , то
, то 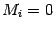 . Таким образом,
. Таким образом,  , что противоречит определению базисного минора. Значит, предположение, что
, что противоречит определению базисного минора. Значит, предположение, что 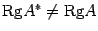 , неверно.
, неверно.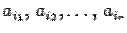 . Тогда по теореме о базисном миноре в матрице
. Тогда по теореме о базисном миноре в матрице 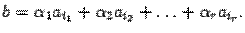
 ,
, 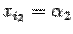 ,
,  ,
, 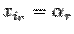 , остальные неизвестные возьмем равными нулю. Тогда при этих значениях
, остальные неизвестные возьмем равными нулю. Тогда при этих значениях 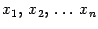 получим
получим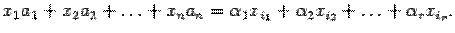
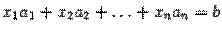 . Последнее равенство означает, что набор чисел
. Последнее равенство означает, что набор чисел  является решением системы. Существование решения доказано.
является решением системы. Существование решения доказано.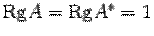 , и система является совместной. В системе
, и система является совместной. В системе  ,
,  , и система является несовместной.
, и система является несовместной. и
и 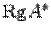 , ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.
, ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна. линейных уравнений с
линейных уравнений с  неизвестными
неизвестными 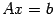 . Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя и к методу нахождения ранга матрицы. Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.
. Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя и к методу нахождения ранга матрицы. Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.
 . Тогда ко второй строке прибавим первую, умноженную на число
. Тогда ко второй строке прибавим первую, умноженную на число 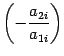 , к третьей строке прибавим первую, умноженную на число
, к третьей строке прибавим первую, умноженную на число 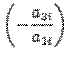 , и т.д. В результате получим матрицу
, и т.д. В результате получим матрицу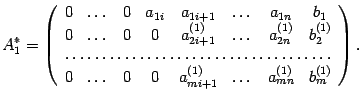
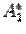 встретилась строка с номером k, в которой все элементы
встретилась строка с номером k, в которой все элементы 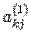 равны нулю, а
равны нулю, а 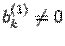 , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что
, то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что 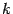 -ое уравнение будет иметь вид
-ое уравнение будет иметь вид 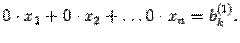
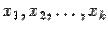 .
. можно записать в виде
можно записать в виде 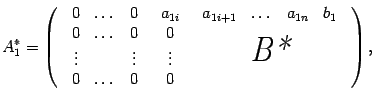

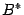 выполняем описанный шаг алгоритма. Получаем матрицу
выполняем описанный шаг алгоритма. Получаем матрицу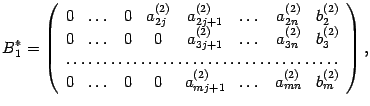
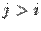 ,
, 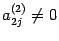 . Эту матрицу снова можно записать в виде
. Эту матрицу снова можно записать в виде
 снова применим описанный выше шаг алгоритма.
снова применим описанный выше шаг алгоритма.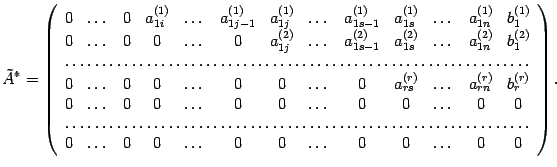
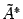 составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть
составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть  . Заметим, что
. Заметим, что 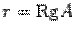 . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.
. Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.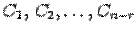 , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин
, включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин 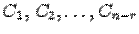 (в частности, просто произвольной величиной
(в частности, просто произвольной величиной 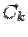 ). Эта запись и будет общим решением системы.
). Эта запись и будет общим решением системы.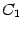 , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при
, взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при  -- второе решение и т.д.
-- второе решение и т.д.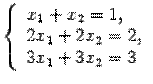
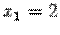 ,
, 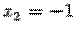 и даже имеет бесконечно много решений, а система из двух уравнений с тремя неизвестными
и даже имеет бесконечно много решений, а система из двух уравнений с тремя неизвестными

 , то в силу предложения 14.26 (Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему)
, то в силу предложения 14.26 (Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему)  .
. ,
, 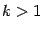 . Тогда в матрице
. Тогда в матрице  . Получили противоречие. Предположение, что k>1, неверно.
. Получили противоречие. Предположение, что k>1, неверно.
 A11x1 + … + a1nxn = 0
A11x1 + … + a1nxn = 0
 Хr (1), Х(2) =
Хr (1), Х(2) =  A11x1 + … + a1nxn = 0
A11x1 + … + a1nxn = 0


