
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление функций одной переменной
Понятие производной Пусть функция y = f (x) определена в точке x0 и некоторой ее окрестности, x – точка из этой окрестности. Введем обозначения: разность x – x0 обозначим через Итак, Производной функции f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Производная обозначается f'(x0). Итак, Пример 1. Найти производную для функции f(x) = x2 в точке x0 = 3.
Переформулируем это определение, используя понятия приращения аргумента и приращения функции. Из этого равенства получаем:
Другими словами, функция f (x) непрерывна в точке x0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Теорема. Если функция f(x) дифференцируема в точке x0, то она непрерывна в этой точке. Замечание. Если в точке x0 функция f (x) непрерывна, то в этой точке функция может и не иметь производной.
Основные правила дифференцирования 1. Постоянный множитель c можно выносить за знак производной: 2. Если существуют производные u'(x) и v'(x), то производная от суммы (разности) функций u(x) и v(x) равна сумме (разности) производных: 3. Если существуют производные u'(x) и v'(x), то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
Формулы дифференцирования основных функций Правила Лопиталя Пусть функции y=f(x) и y=g(x) удовлетворяют следующим условиям: 1) эти функции дифференцируемы в окрестности точки a, кроме, может быть, самой точки a; 2) 3) 4) Тогда существует
Замечание 1. Правило Лопиталя распространяется на случай неопределенности типа Замечание 2. Правило Лопиталя распространяется и на случай Замечание 3. Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми. Замечание 4. Хотя правило Лопиталя работает только с неопределенностями
Понятие экстремума функции Определение. Точка x0 называется точкой локального максимума функции f(x), если существует такая окрестность этой точки, что для всех x из этой окрестности выполняется неравенство: Определение. Точка x0 называется точкой локального минимума функции f(x), если существует такая окрестность этой точки, что для всех x из этой окрестности Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальнымминимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами. Точка x0 называется точкой строгого локального максимума функции y=f(x), если для всех x из окрестности этой точки будет справедливо строгое неравенство Точка x0 называется точкой строгого локального минимума функции y=f(x), если для всех x из окрестности этой точки будет справедливо строгое неравенство
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом. Необходимое условие экстремума Если функция y=f(x) имеет экстремум в точке x0, то ее производная Точки, в которых производная равна нулю: Замечание Не в каждой своей критической точке функция обязательно имеет максимум или минимум. Первое достаточное условие экстремума Теорема (Первое достаточное условие экстремума)
1.функция непрерывна в окрестности точки x0; Если производная Таким образом, для того чтобы исследовать функцию y=f(x) на экстремум, необходимо: 1.найти производную Второе достаточное условие экстремума Теорема (Второе достаточное условие экстремума) 1.она непрерывна в окрестности точки x0; Тогда в точке x0 достигается экстремум, причем, если
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.195 (0.01 с.) |
 x и назовем приращением аргумента, а разность f(x) – f(x0) обозначим через
x и назовем приращением аргумента, а разность f(x) – f(x0) обозначим через 


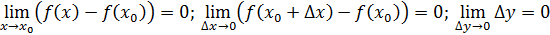





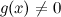 и
и  в этой окрестности;
в этой окрестности;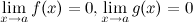 ;
; существует конечный или бесконечный.
существует конечный или бесконечный. и, причем
и, причем 
 при
при  .
. . Чтобы убедится в этом, достаточно сделать замену
. Чтобы убедится в этом, достаточно сделать замену  и воспользоваться результатом выше приведенной теоремы.
и воспользоваться результатом выше приведенной теоремы. и
и  .
. .
. .
. .
. либо равна нулю, либо не существует.
либо равна нулю, либо не существует.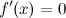 , называются стационарными точками функции.
, называются стационарными точками функции. 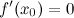 ), либо это точки, в которых производная
), либо это точки, в которых производная  не существует.
не существует. меняет свой знак.
меняет свой знак.  функция y=f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус.
функция y=f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус. в точке x0.
в точке x0. , то в точке
, то в точке  , то в точке
, то в точке 


